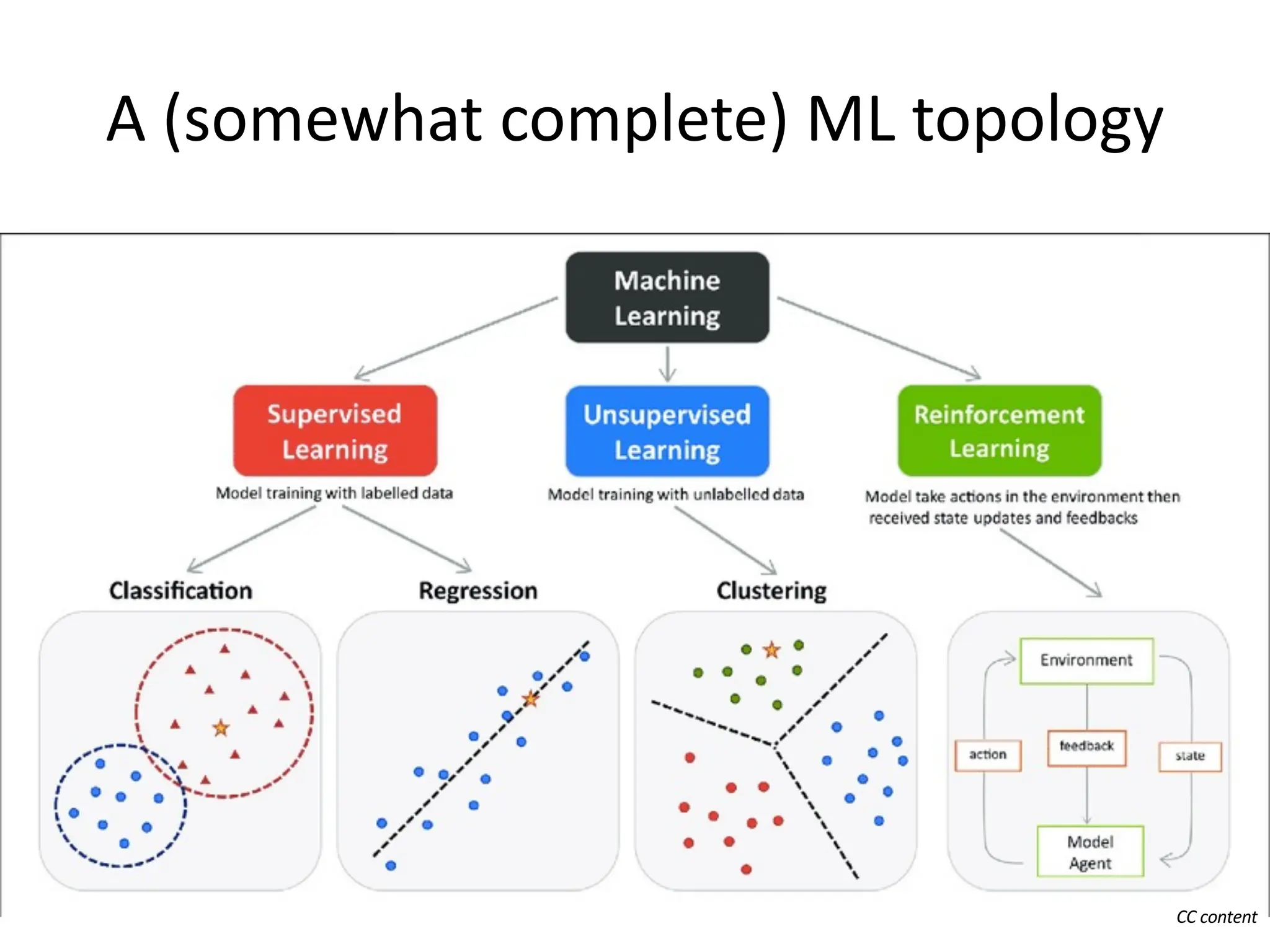
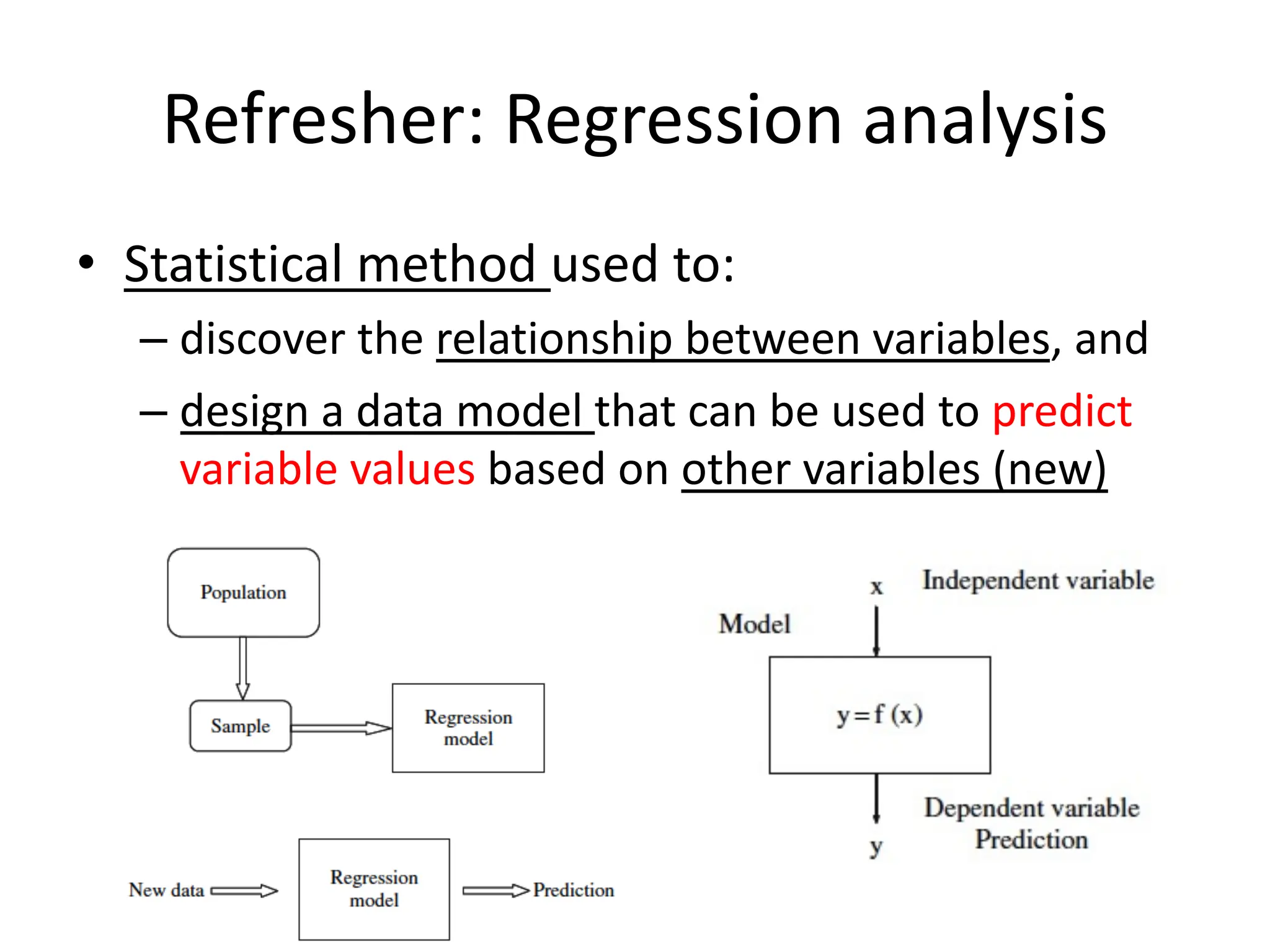
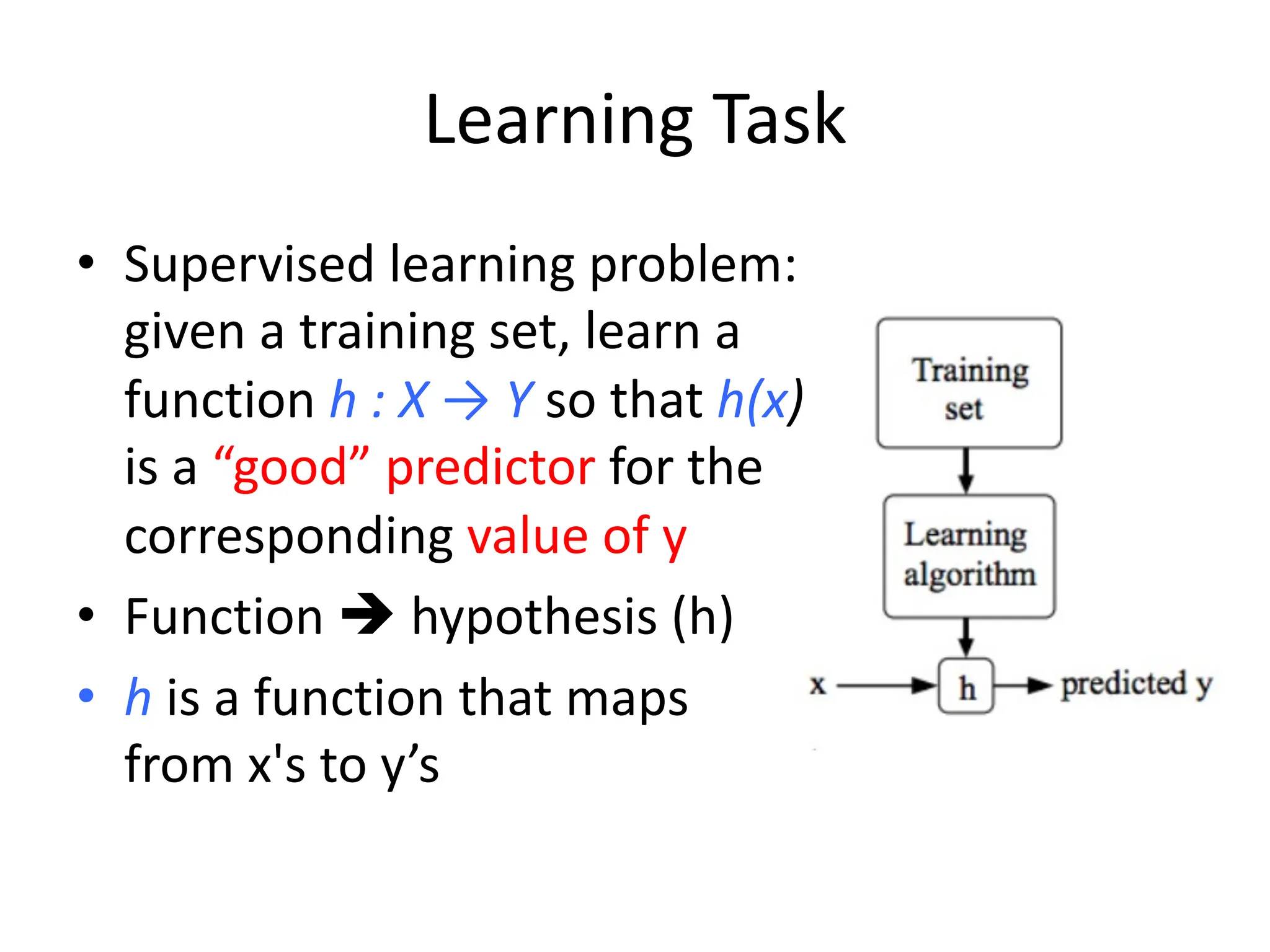
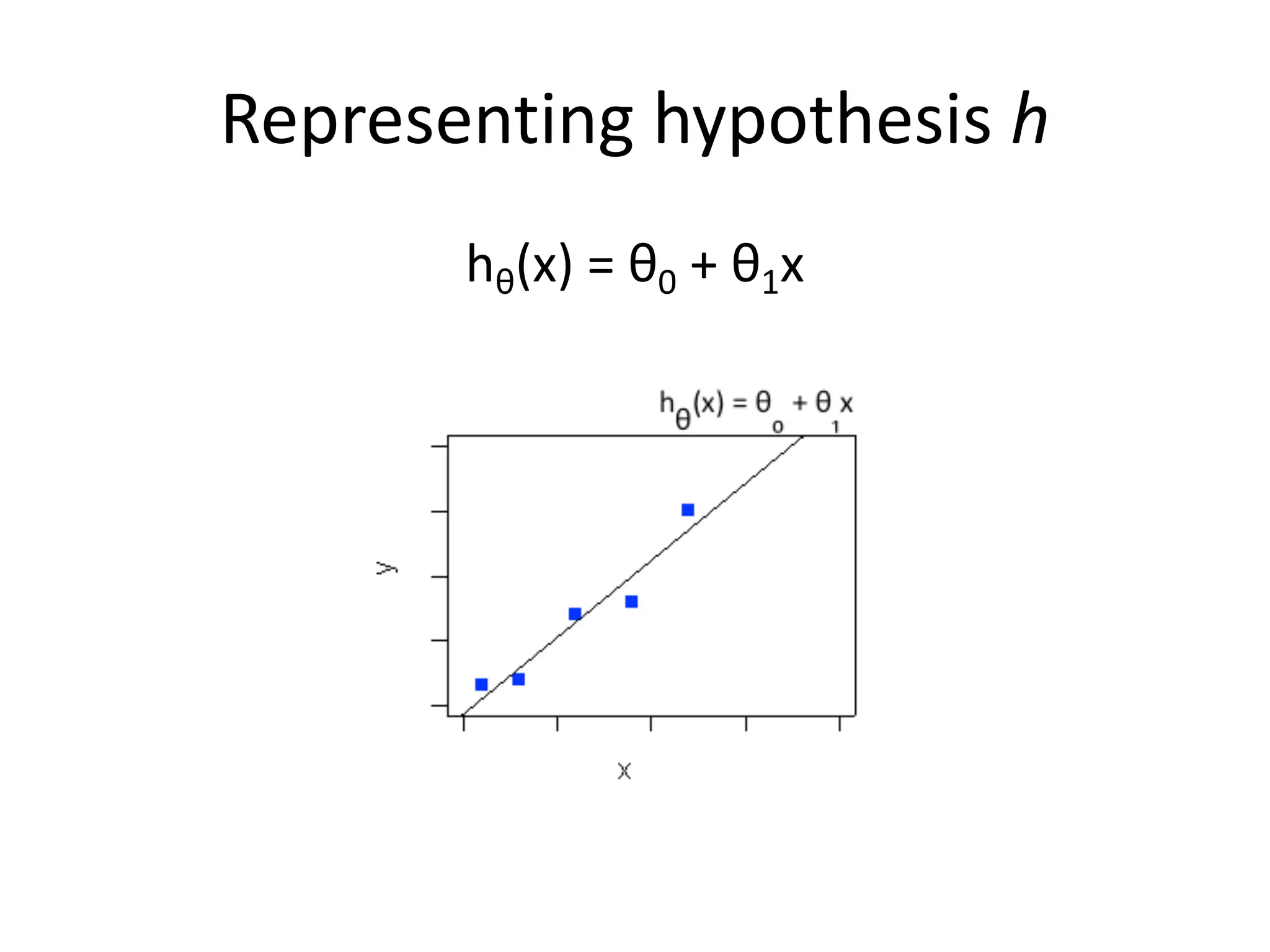
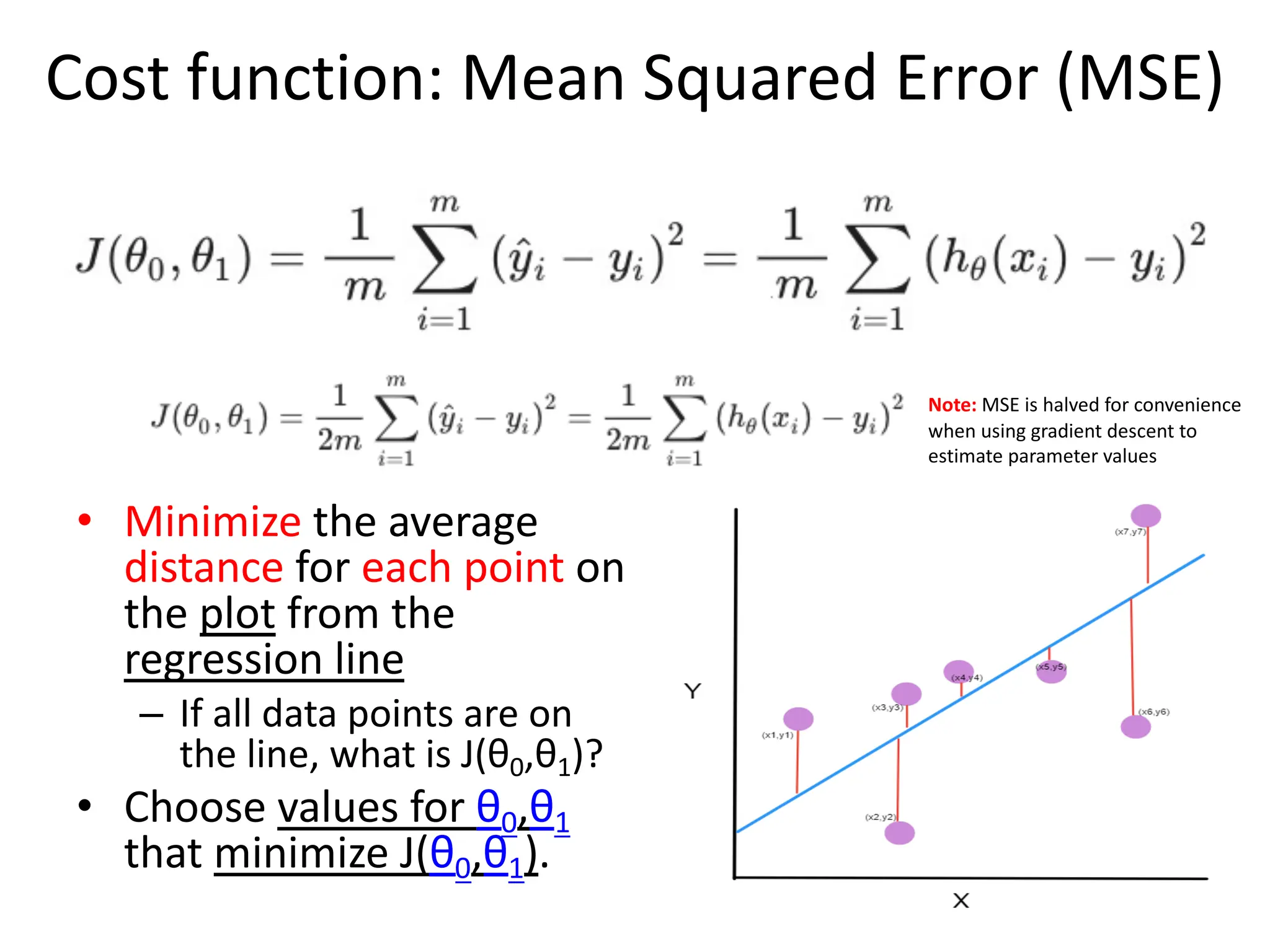
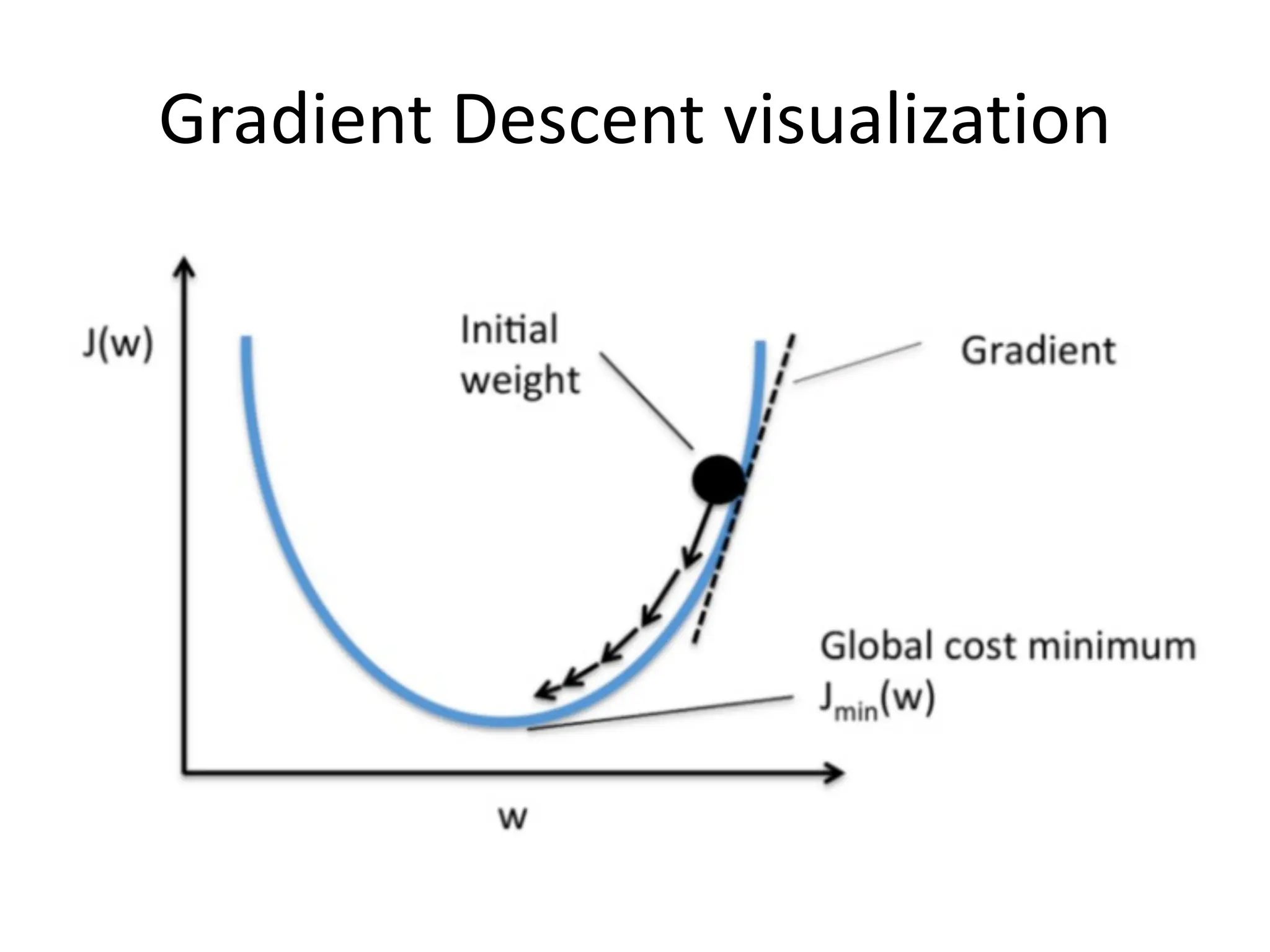
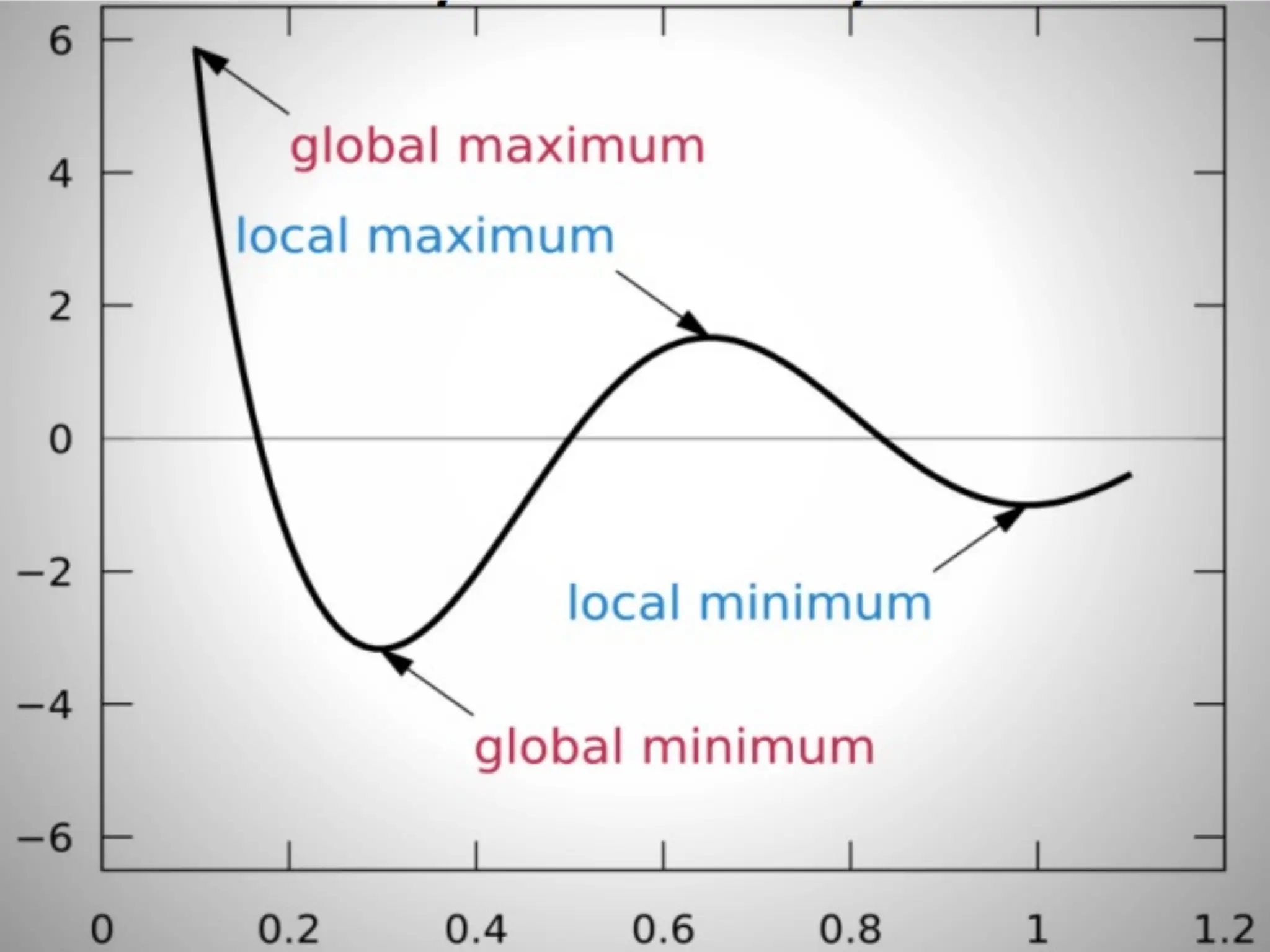
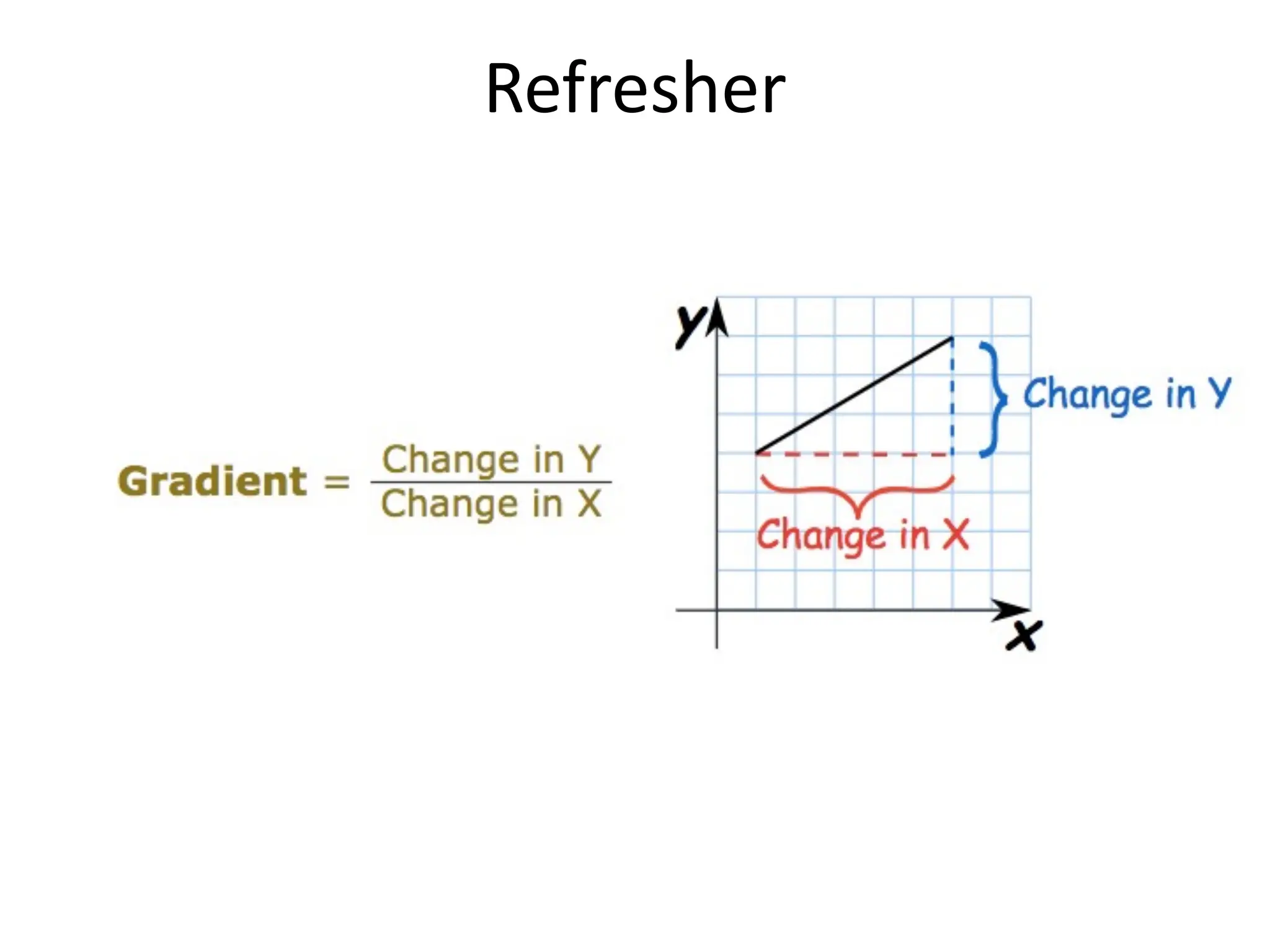
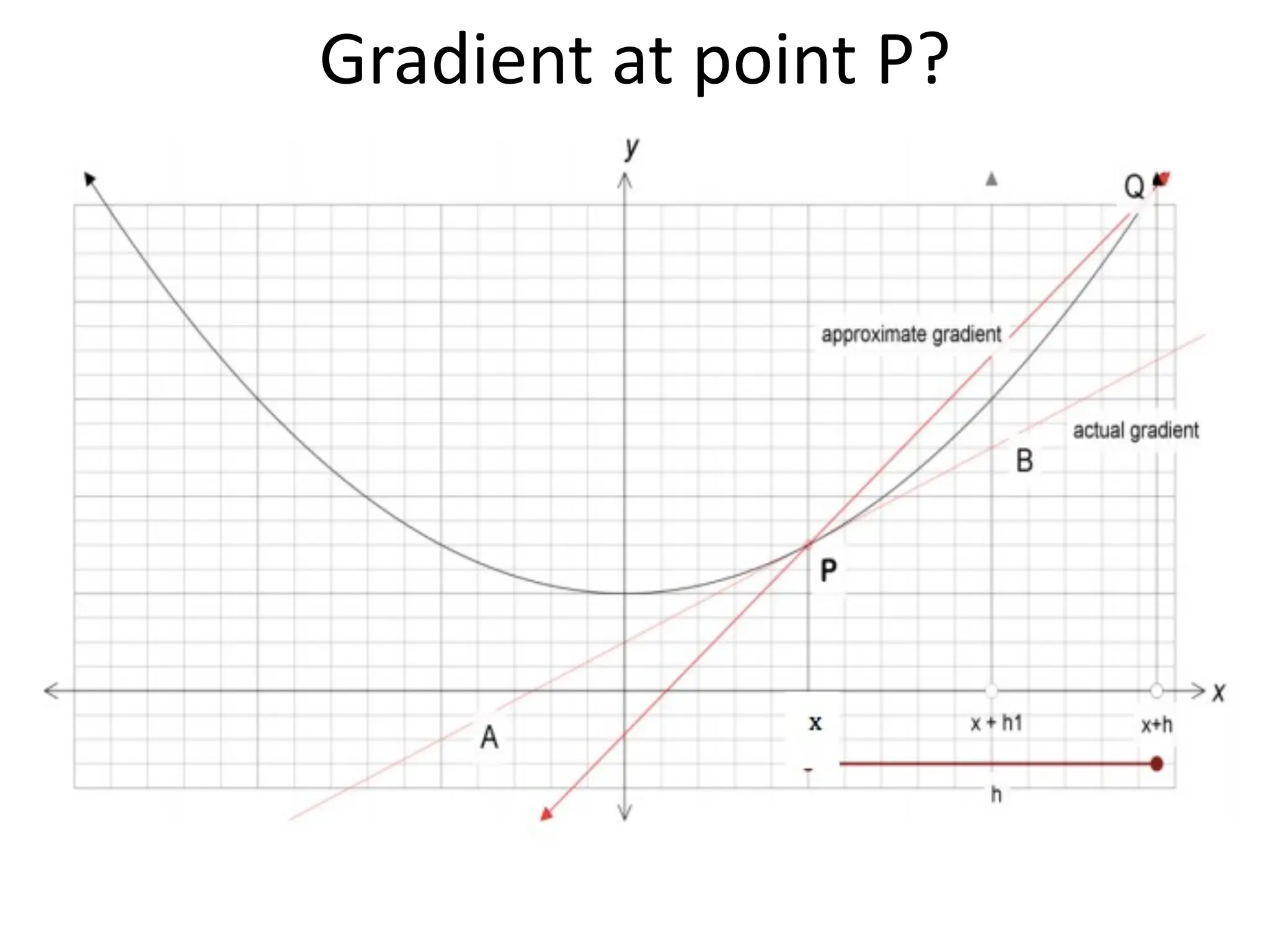
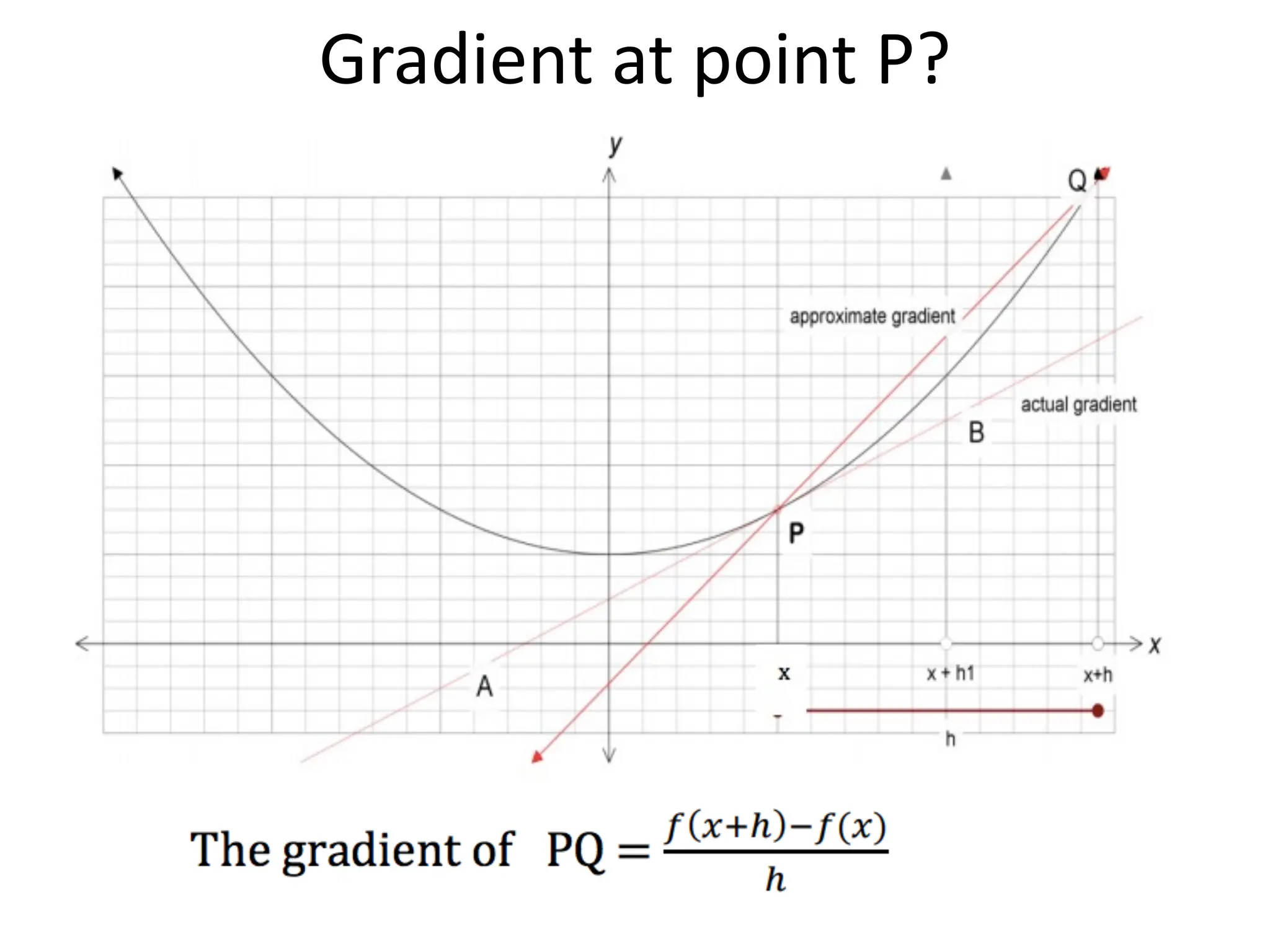
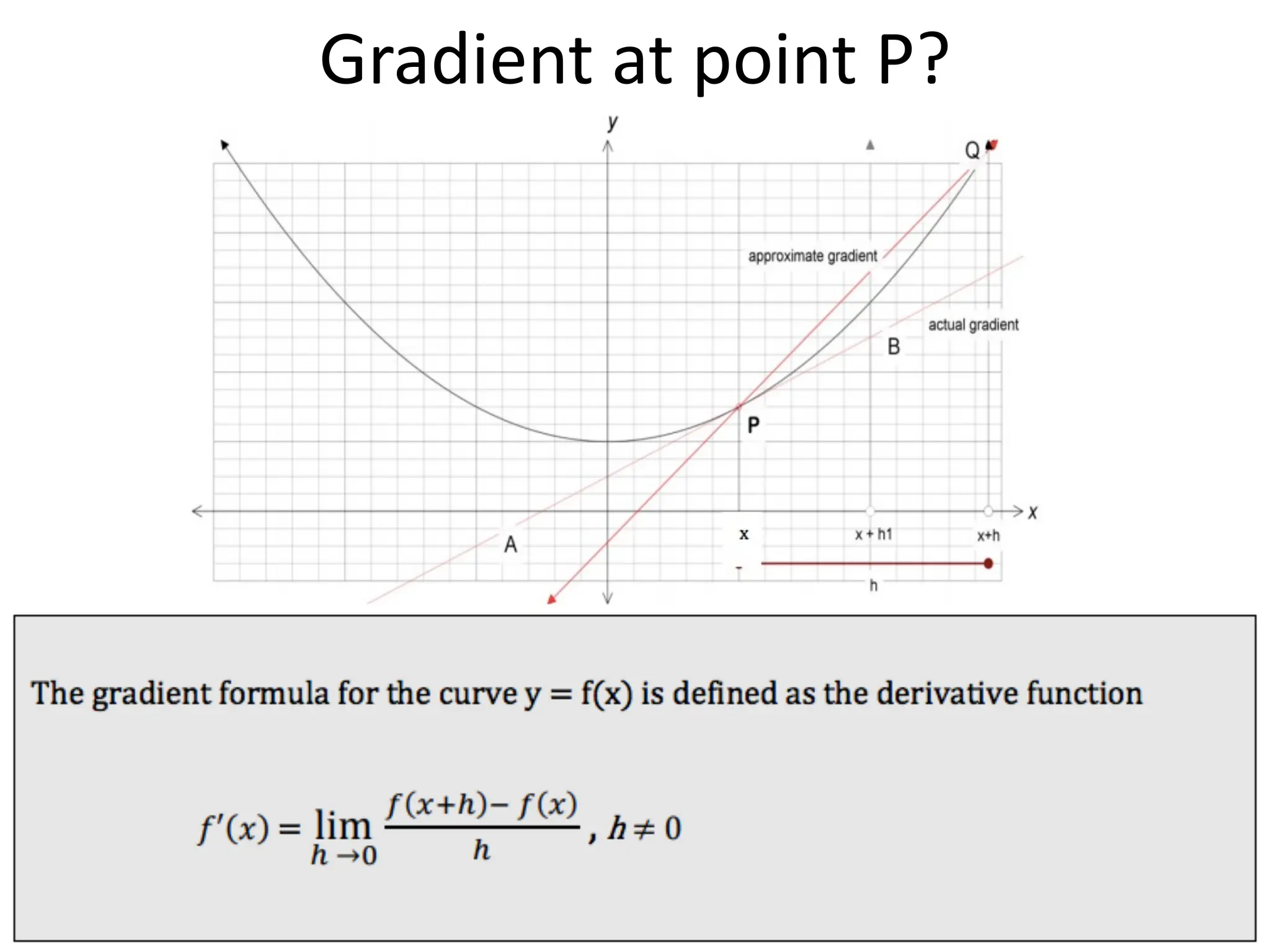
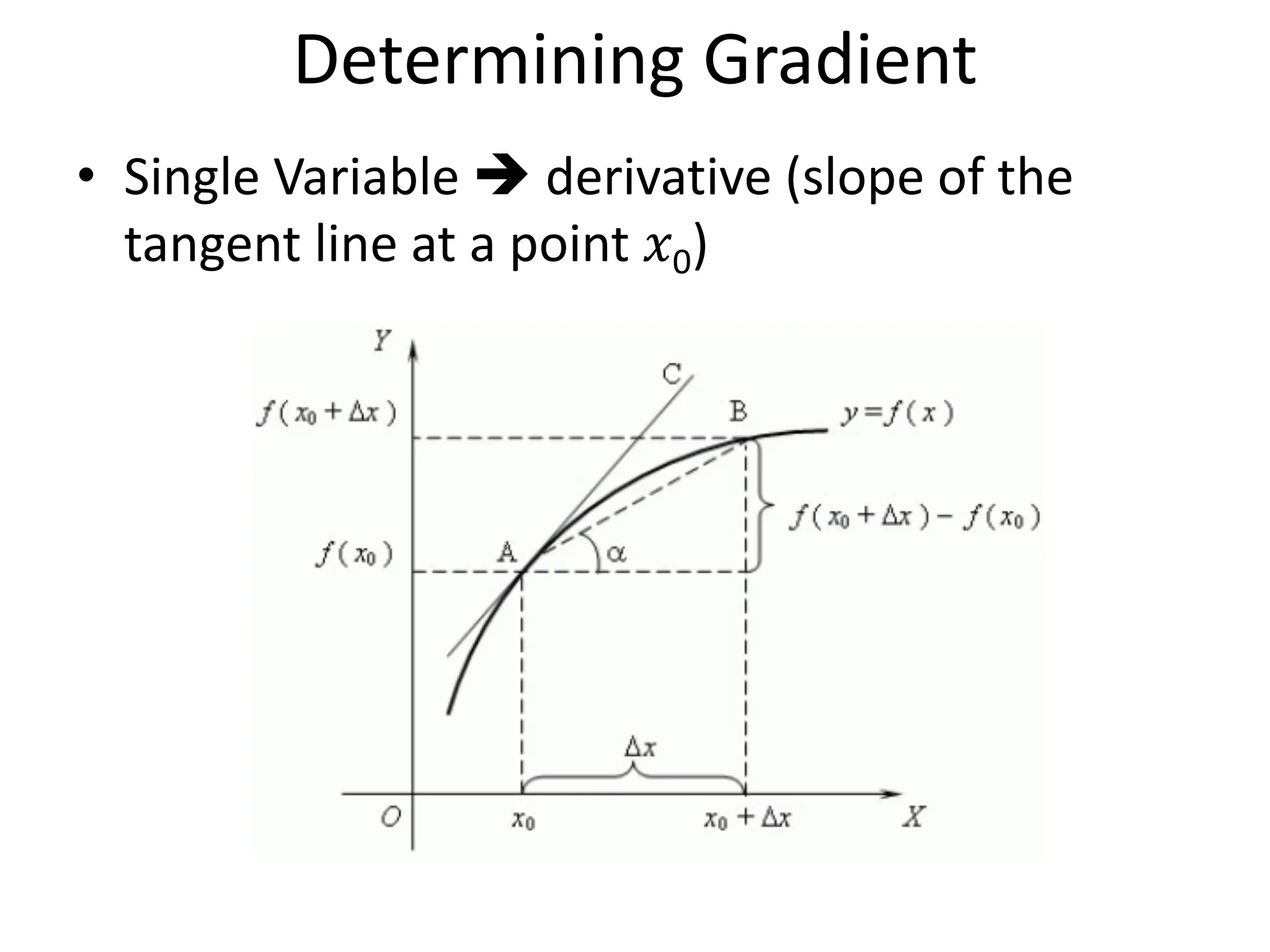
The lecture discusses linear regression as a statistical method for building mathematical models to predict outcomes based on relationships between variables. It emphasizes the importance of model design, parameter learning, and performance evaluation, covering concepts such as univariate and multivariate regression, gradient descent optimization, and performance metrics like mean squared error and coefficient of determination. Additionally, the document highlights preprocessing steps for data to ensure optimal performance of machine learning algorithms.



















![Performance Evaluation • After learning a model, we need to evaluate performance è how well has it learned the task? How good is its generalization performance? – How well does it perform on unseen test data? • How do we evaluate regression models? – Residual plot (residual errors vs. predicted values); residual errors expected to be randomly distributed and scattered around the center (y=0) line – MSE • Compare MSE for training vs. test data • Can be used to compare different regression models • Can be used to tune a given model’s hyper-parameters via grid search and cross-validation (if applicable to model structure) – Co-efficient of Determination (R2): • [0-1]; • gives the percentage variation in y explained by x-variables. A higher coefficient is an indicator of a better goodness of fit for the observations; Measure indicates the likelihood of unseen test data falling within the regression line.](https://image.slidesharecdn.com/lecture5-linearregression-250205063748-6f64a49d/75/Lecture-5-Linear-Regression-Linear-Regression-32-2048.jpg)

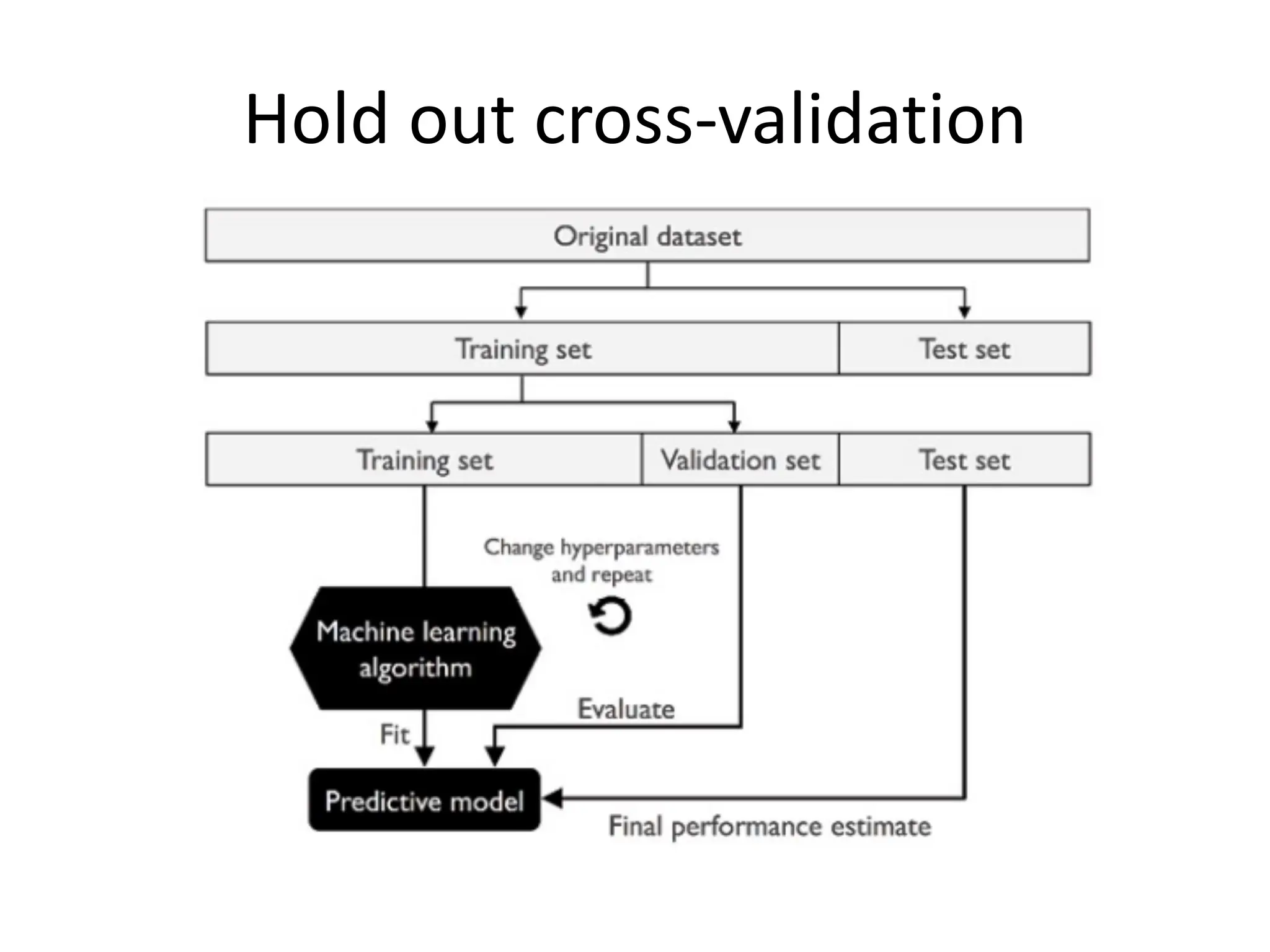
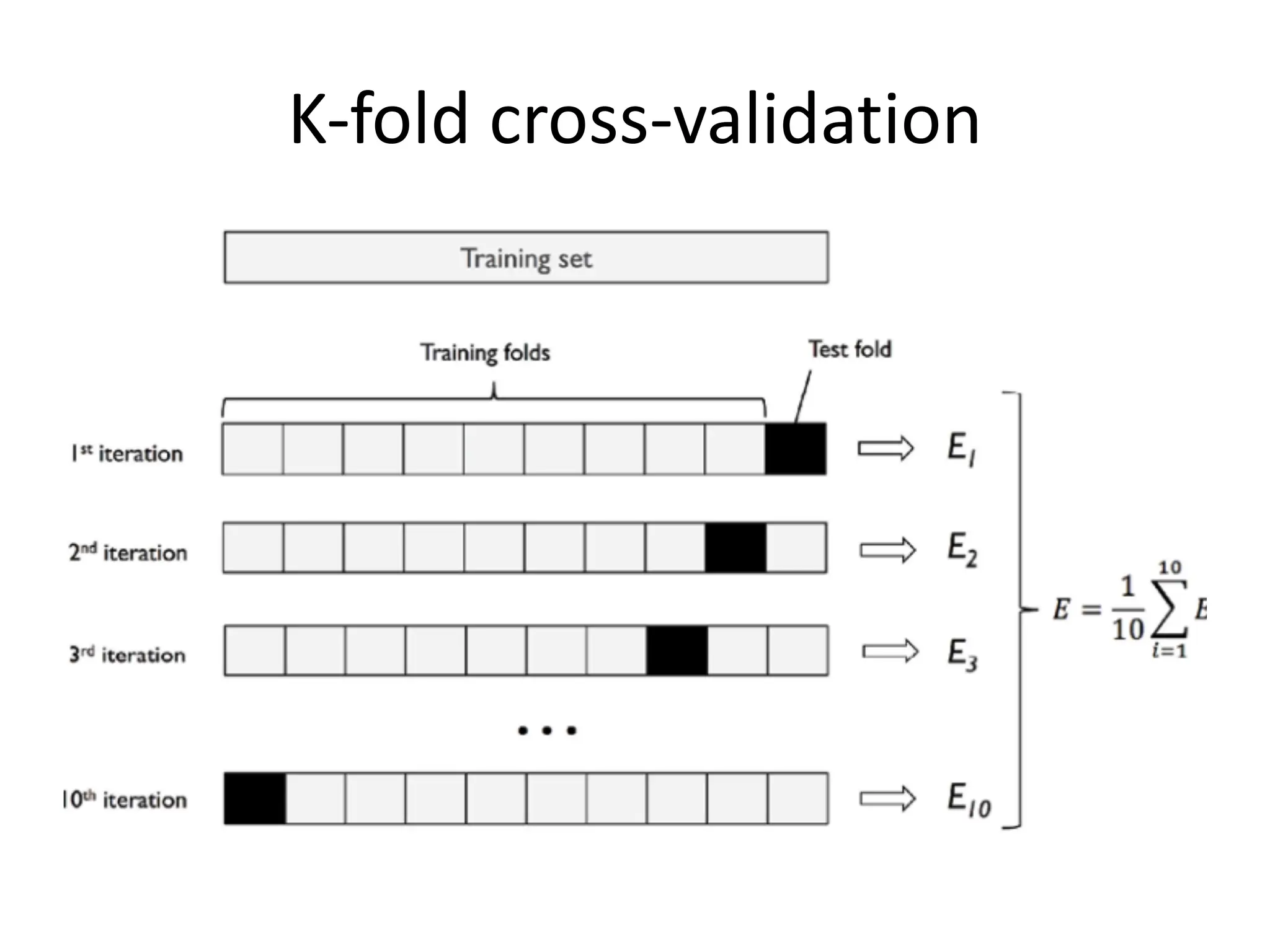
![Preprocessing • Raw data rarely in a shape/form that is necessary for optimal performance of ML algorithms – Preprocessing data thus a crucial first step! • Ensure features selected are on same scale for optimal performance of ML algorithm – Transform features into [0,1] range - normalization – Transform features to attain standard normal distribution with zero mean and unit variance • Dimensionality reduction needed if there’s high correlation between features making them redundant – Improves Signal to Noise ratio (SNR) – Reduces memory requirements – Faster run times for algorithm](https://image.slidesharecdn.com/lecture5-linearregression-250205063748-6f64a49d/75/Lecture-5-Linear-Regression-Linear-Regression-36-2048.jpg)
