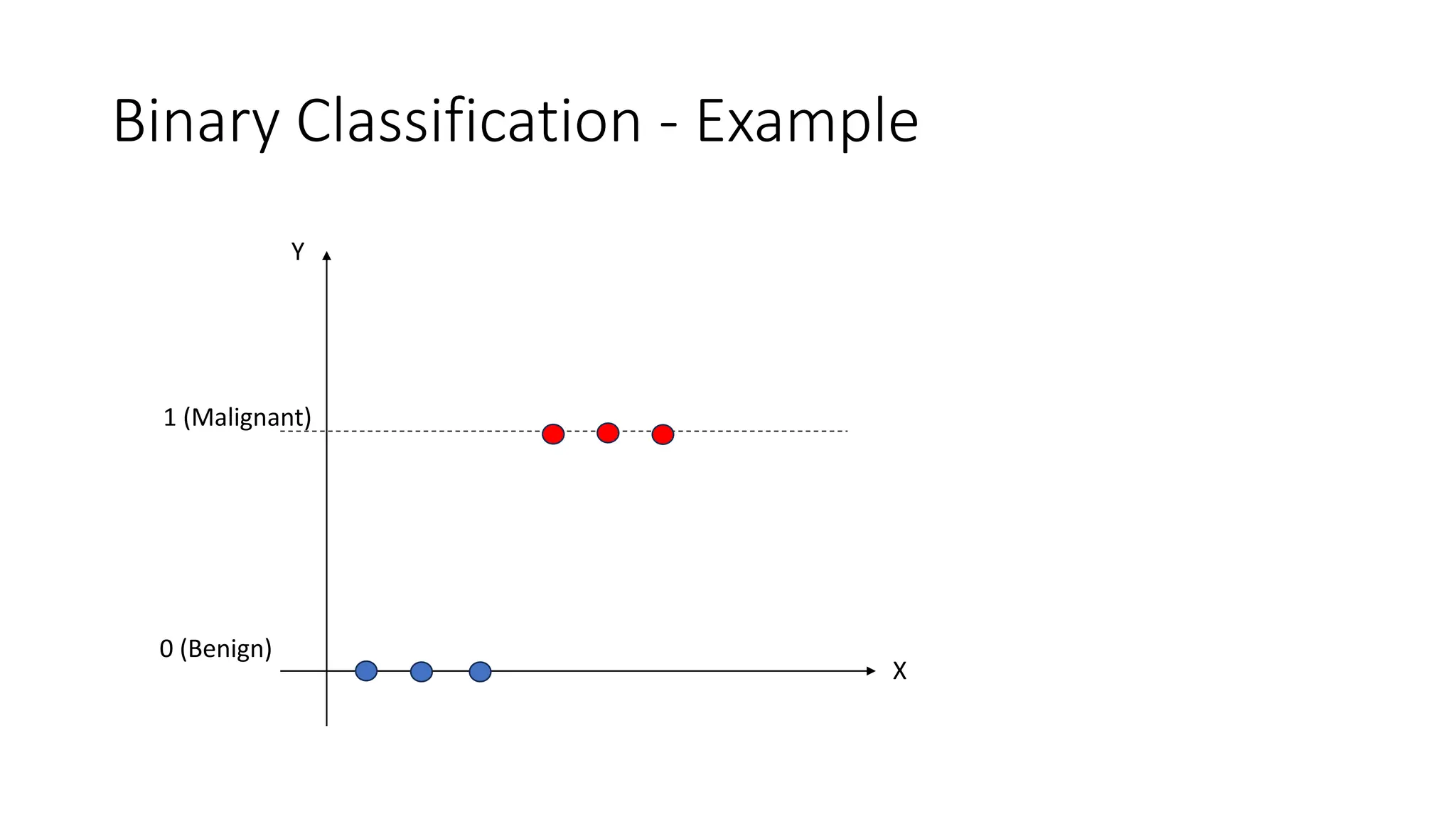
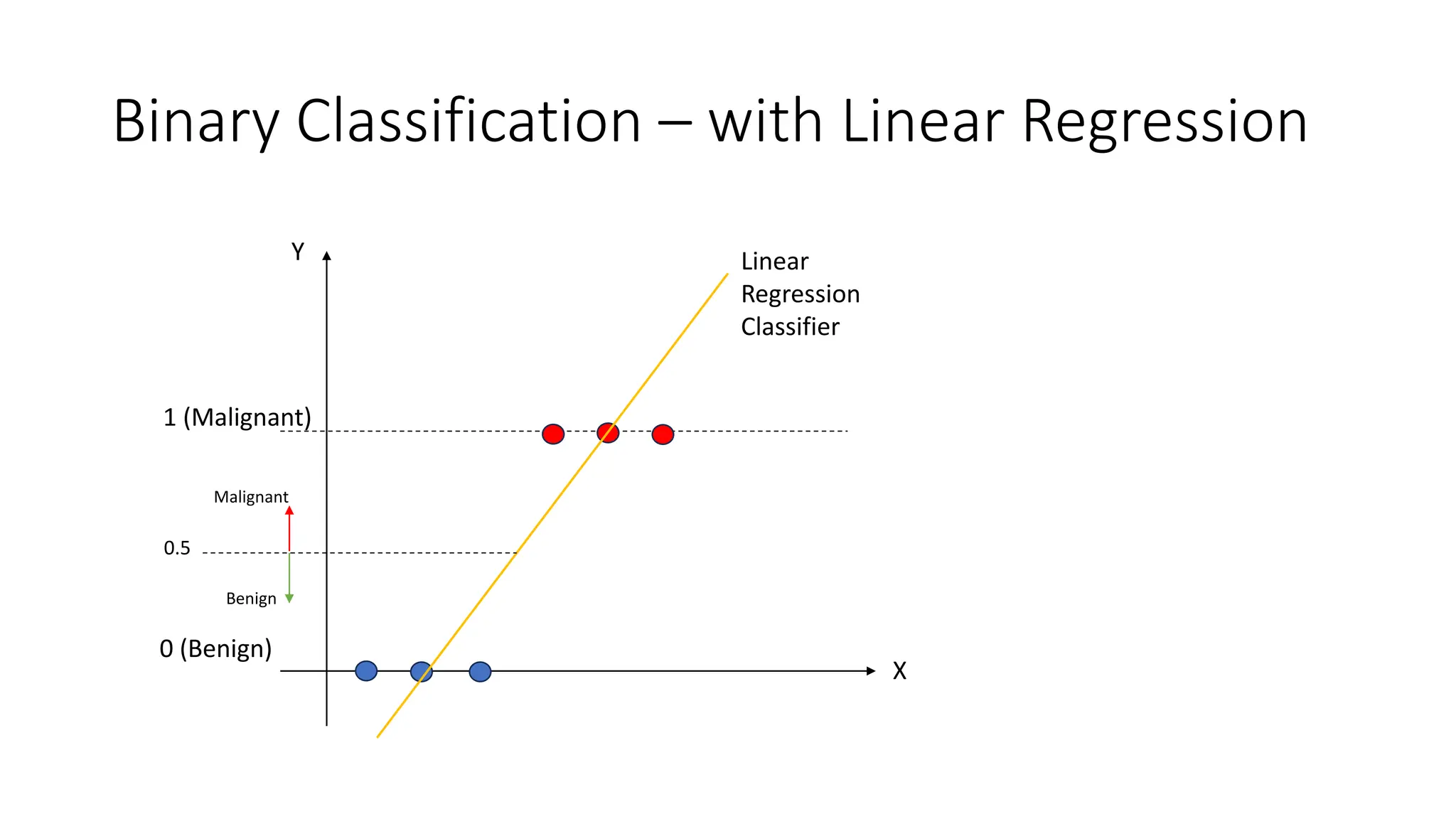
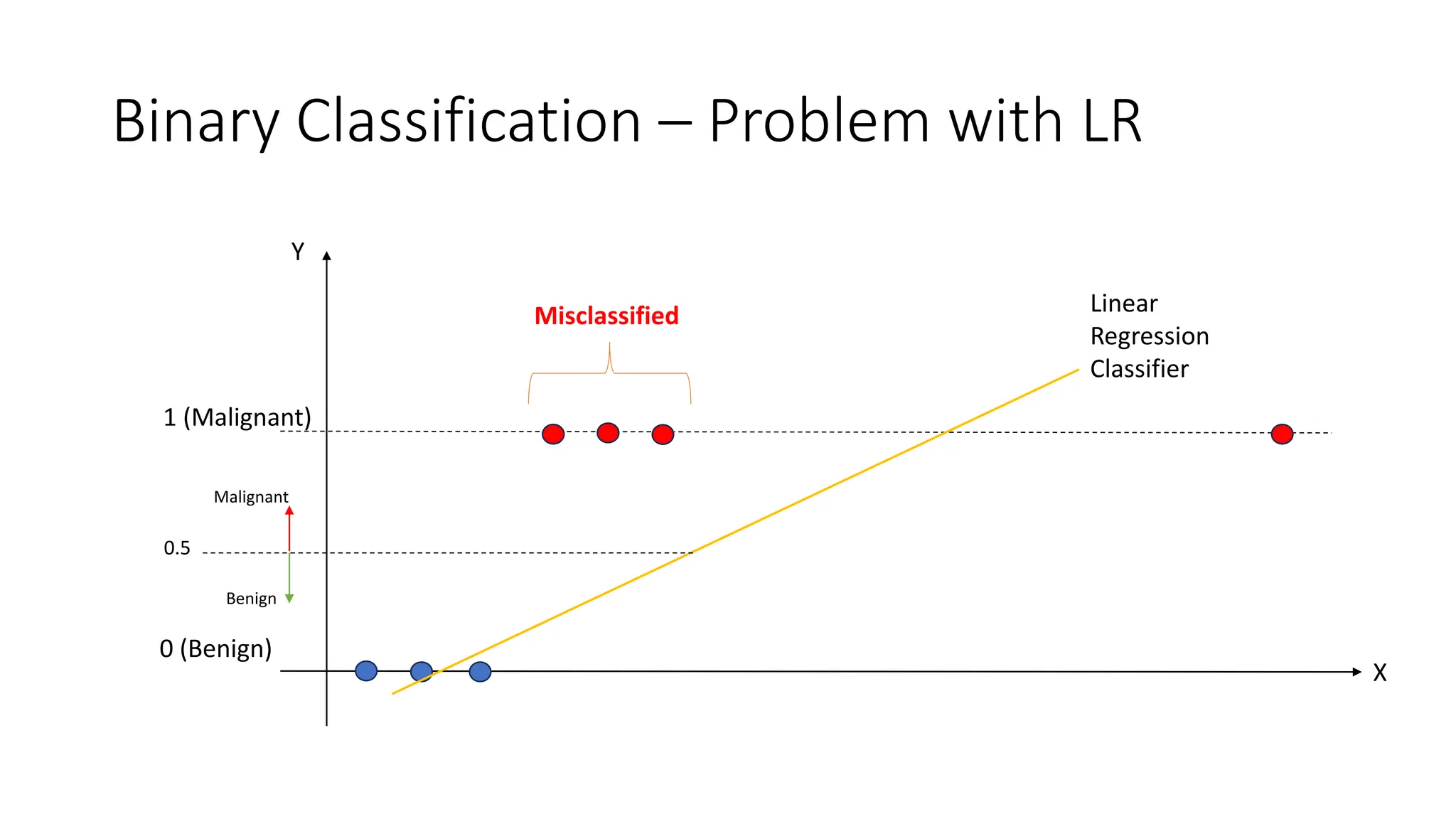
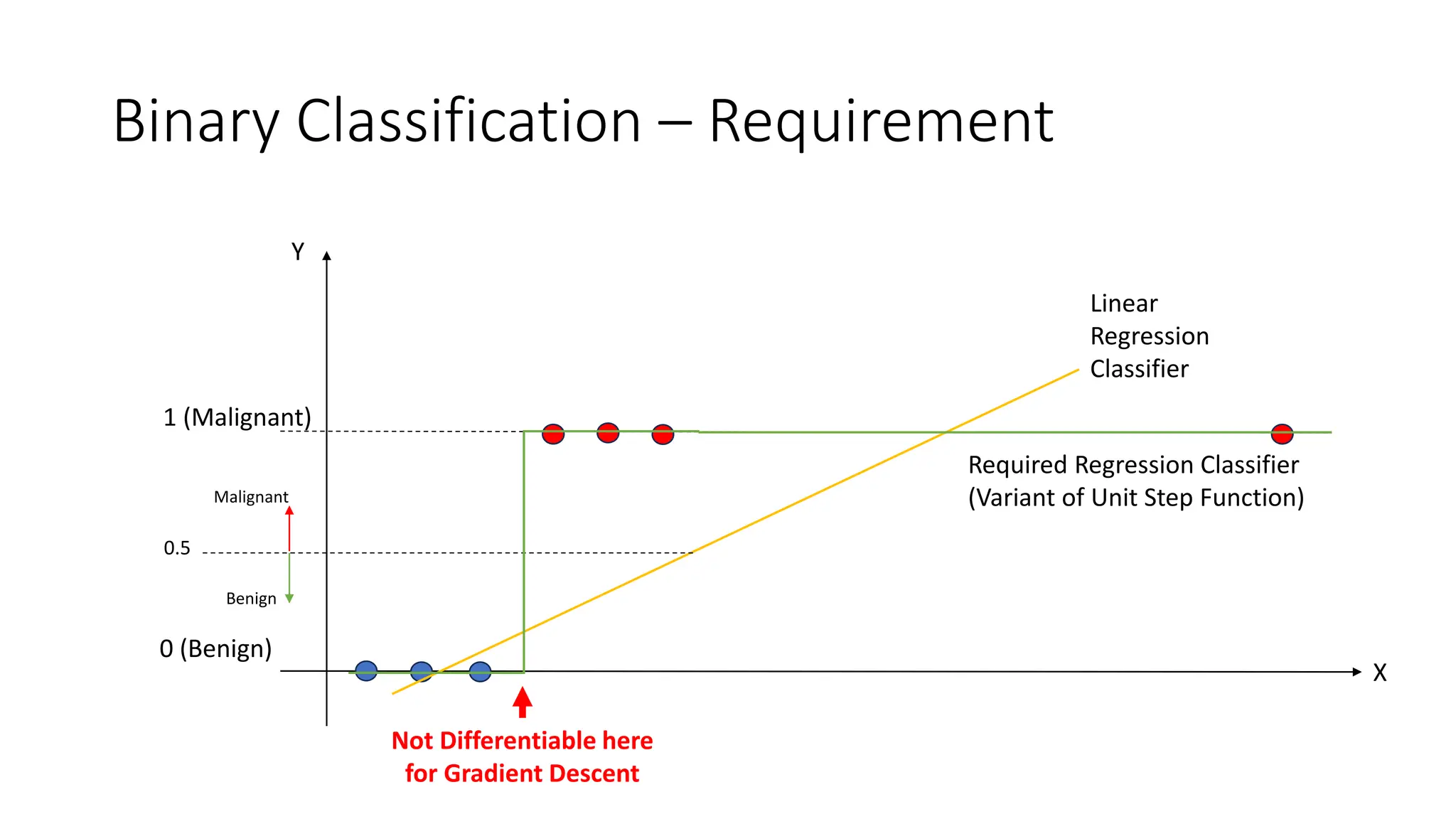
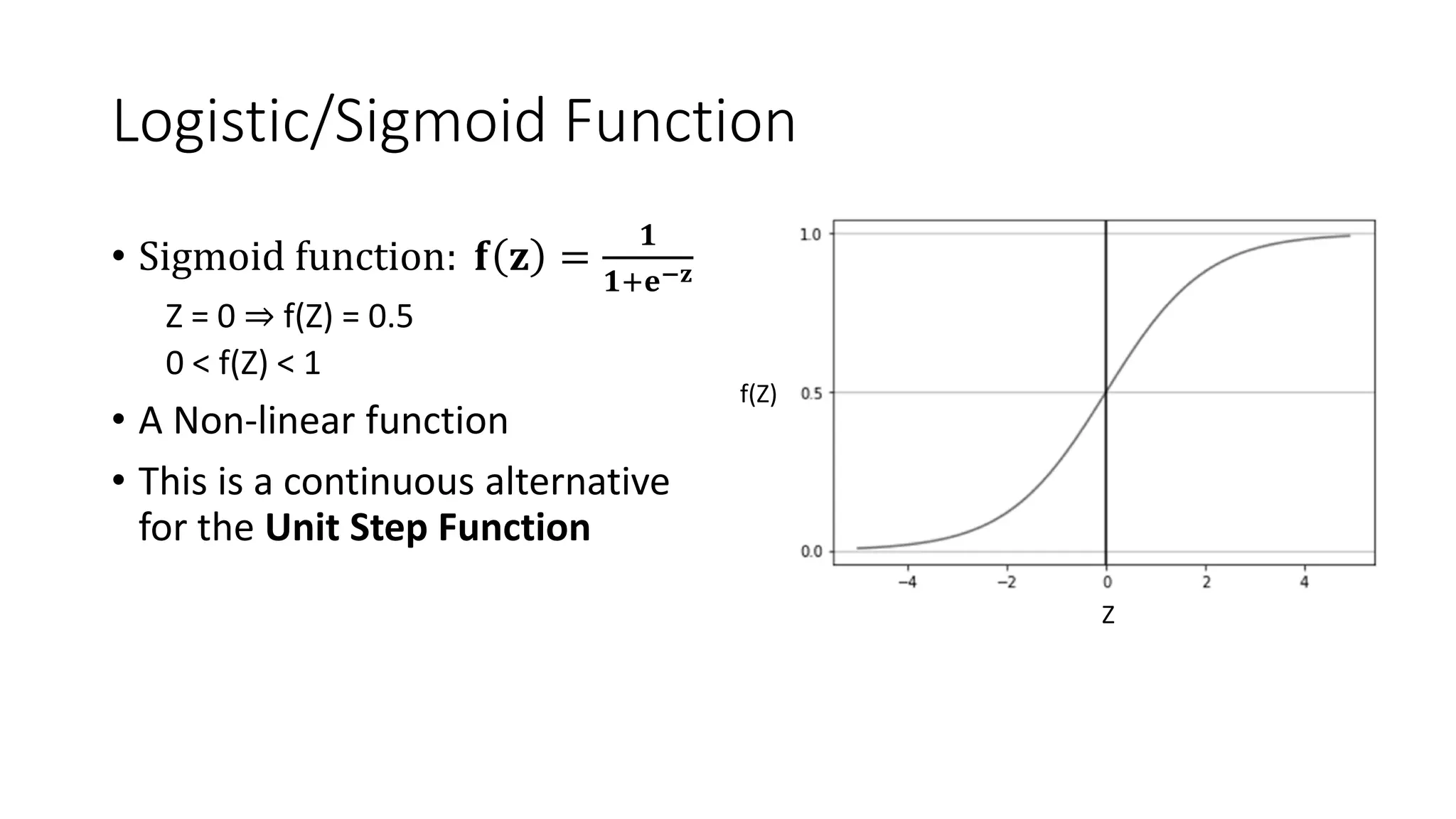
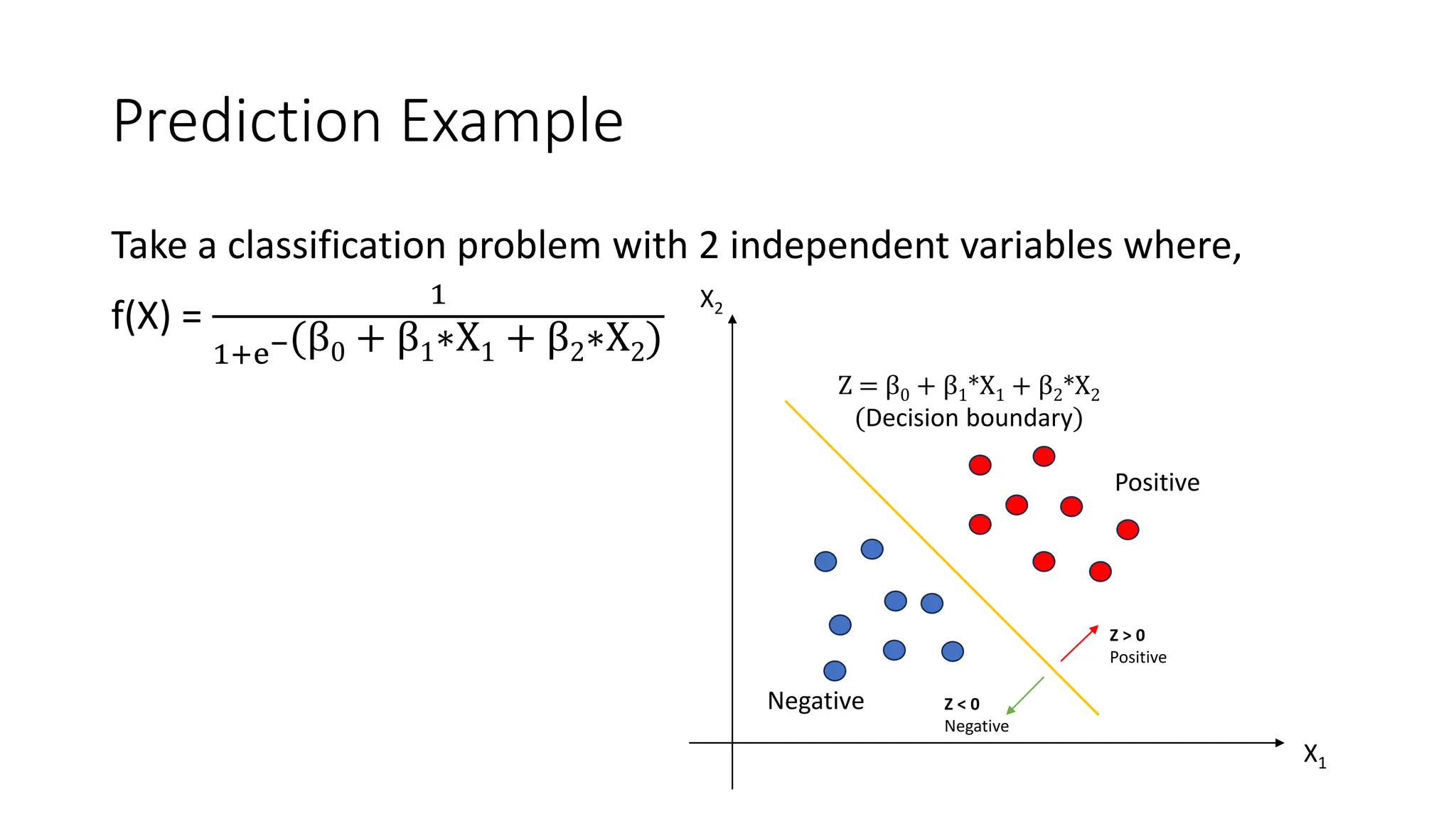
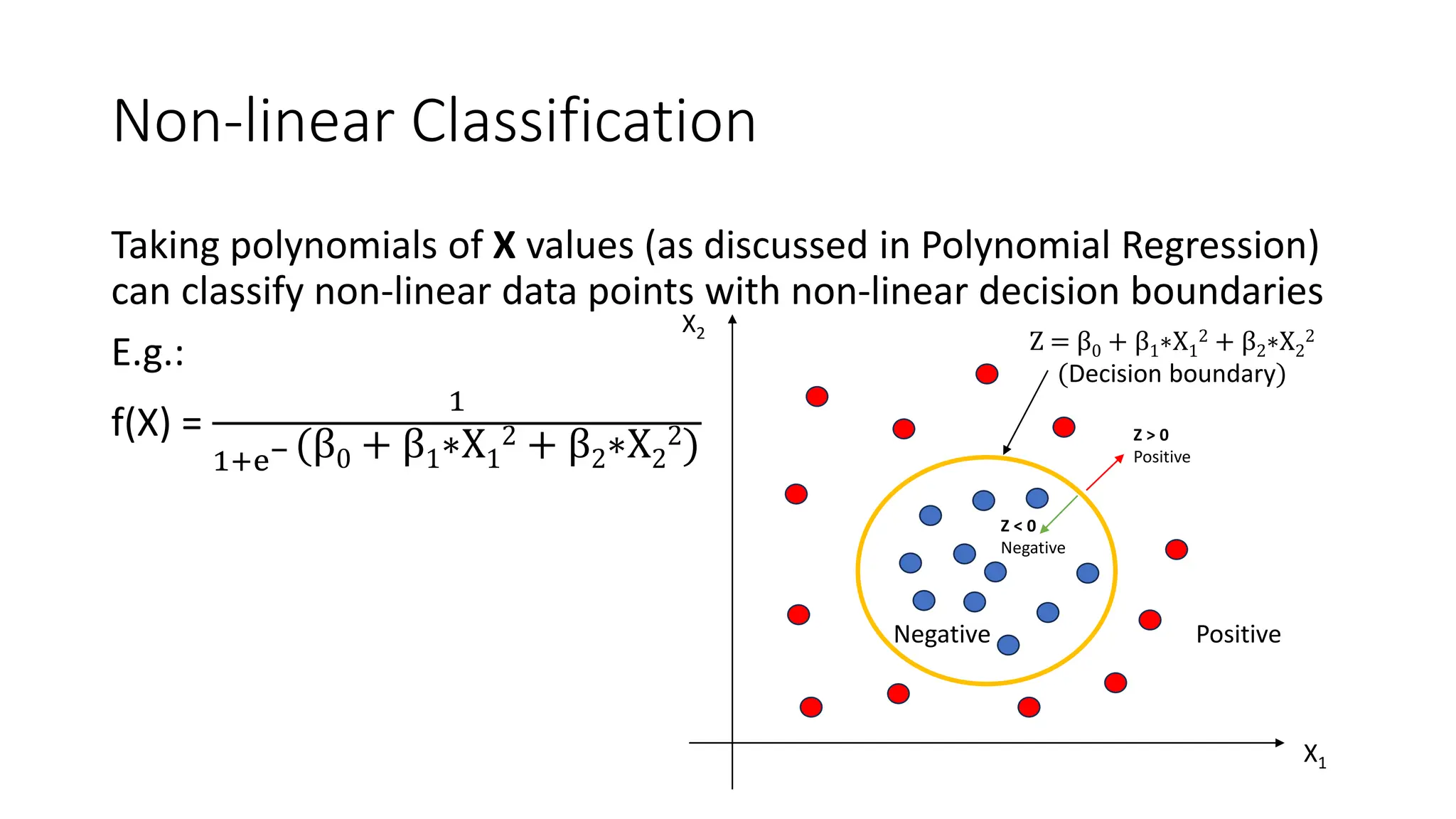
The document covers logistic regression, a statistical method used for classification problems where the dependent variable consists of distinct classes. It details binary classification with examples, discusses the sigmoid function as a continuous alternative to the unit step function, and introduces multiclass logistic regression techniques like one-vs-all and softmax classifiers. The document also addresses cost functions and emphasizes the foundational role of logistic regression in deep neural networks.







![Binary Logistic Regression – Cost Function Cost for a single data point is known as the Loss Take the Loss Function of Logistic Regression as L{f(X)} L f X , Y = ቊ − log f(X) if Y = 1 − log 1 − f(X) if Y = 0 L f X , Y = −Y log f(X) −(1 − Y) log 1 − f(X) Cost function: J(β) = 1 n σ𝑖=1 n L f x , Y J(β) = 1 n 𝑖=1 n [−Y log f(X) − (1 − Y) log 1 − f(X) ] This Cost Function is Convex (has a Global Minimum)](https://image.slidesharecdn.com/lec6-240412205500-3921a10c/75/Lecture-6-Logistic-Regression-a-lecture-in-subject-module-Statistical-Machine-Learning-15-2048.jpg)





![Softmax Regression Loss function: L f X , Y = -log( Yk) = -log( eZ𝑘 j=1 K e Zj ) = -log( eβk TX j=1 K e βj TX ) Cost function (Cross Entropy Loss): J(β) = − ා 𝑖=1 N Σk=1 K I[Yi = k]log( eβk TX j=1 K e βj TX )](https://image.slidesharecdn.com/lec6-240412205500-3921a10c/75/Lecture-6-Logistic-Regression-a-lecture-in-subject-module-Statistical-Machine-Learning-21-2048.jpg)

