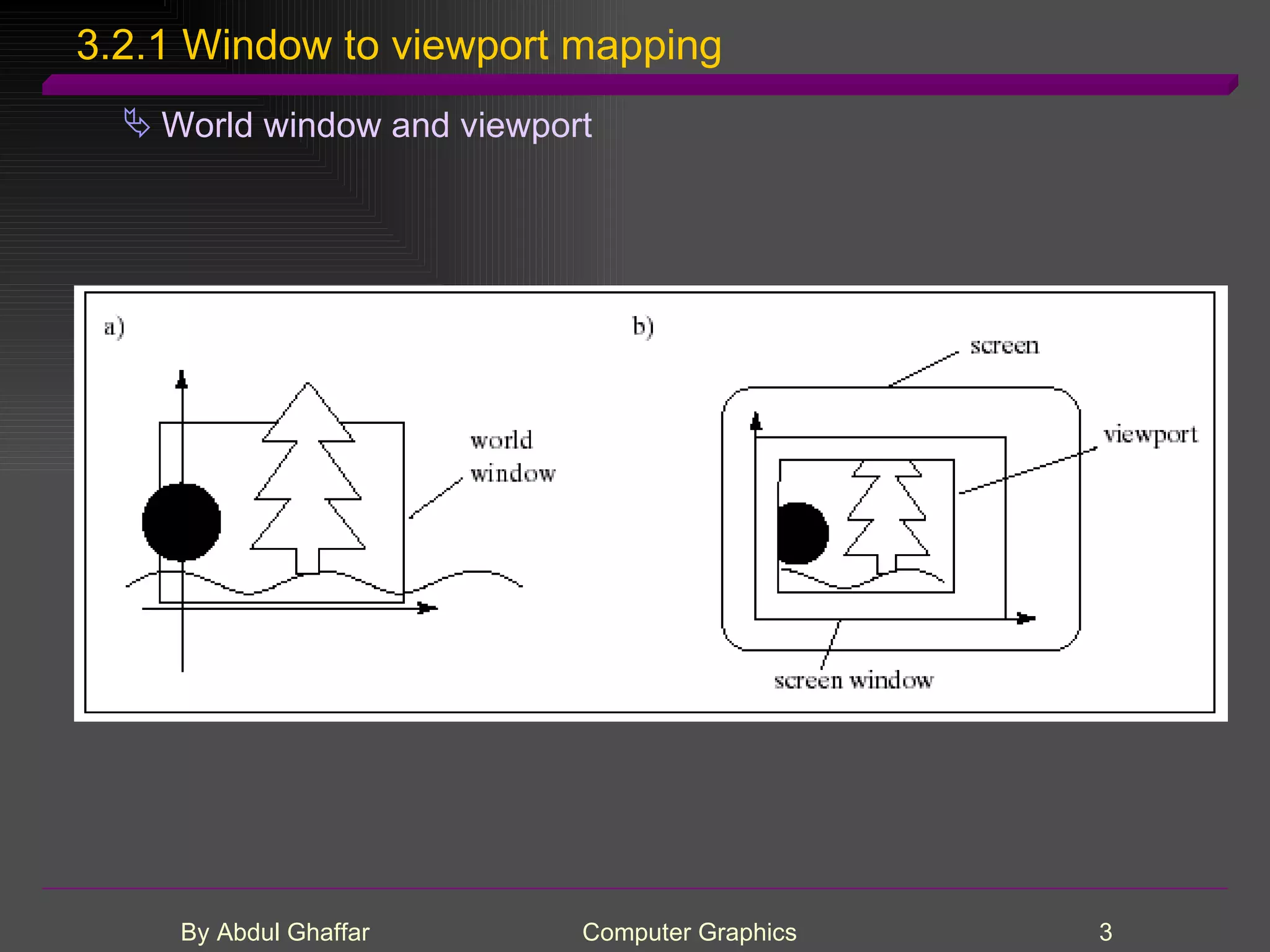
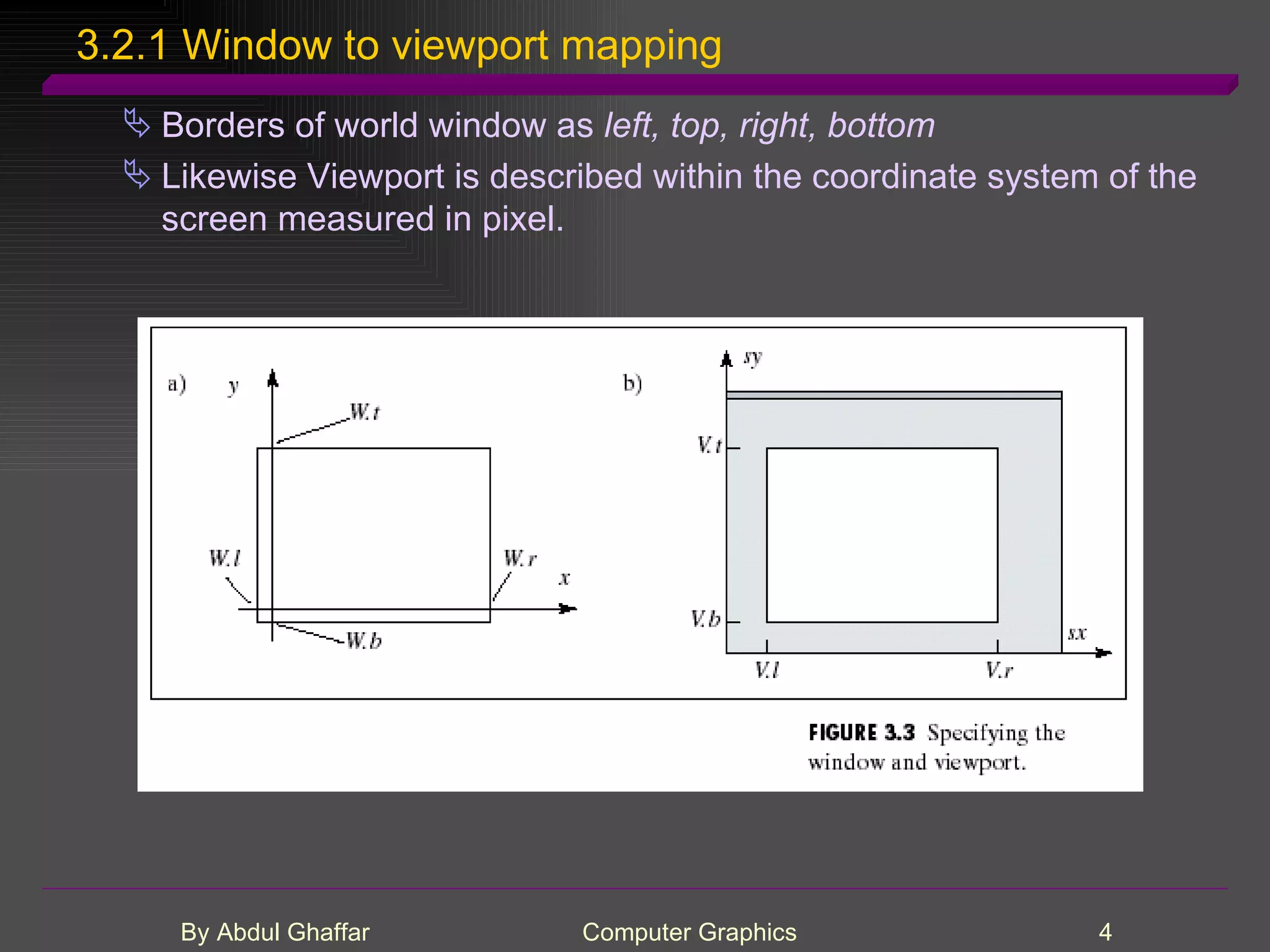
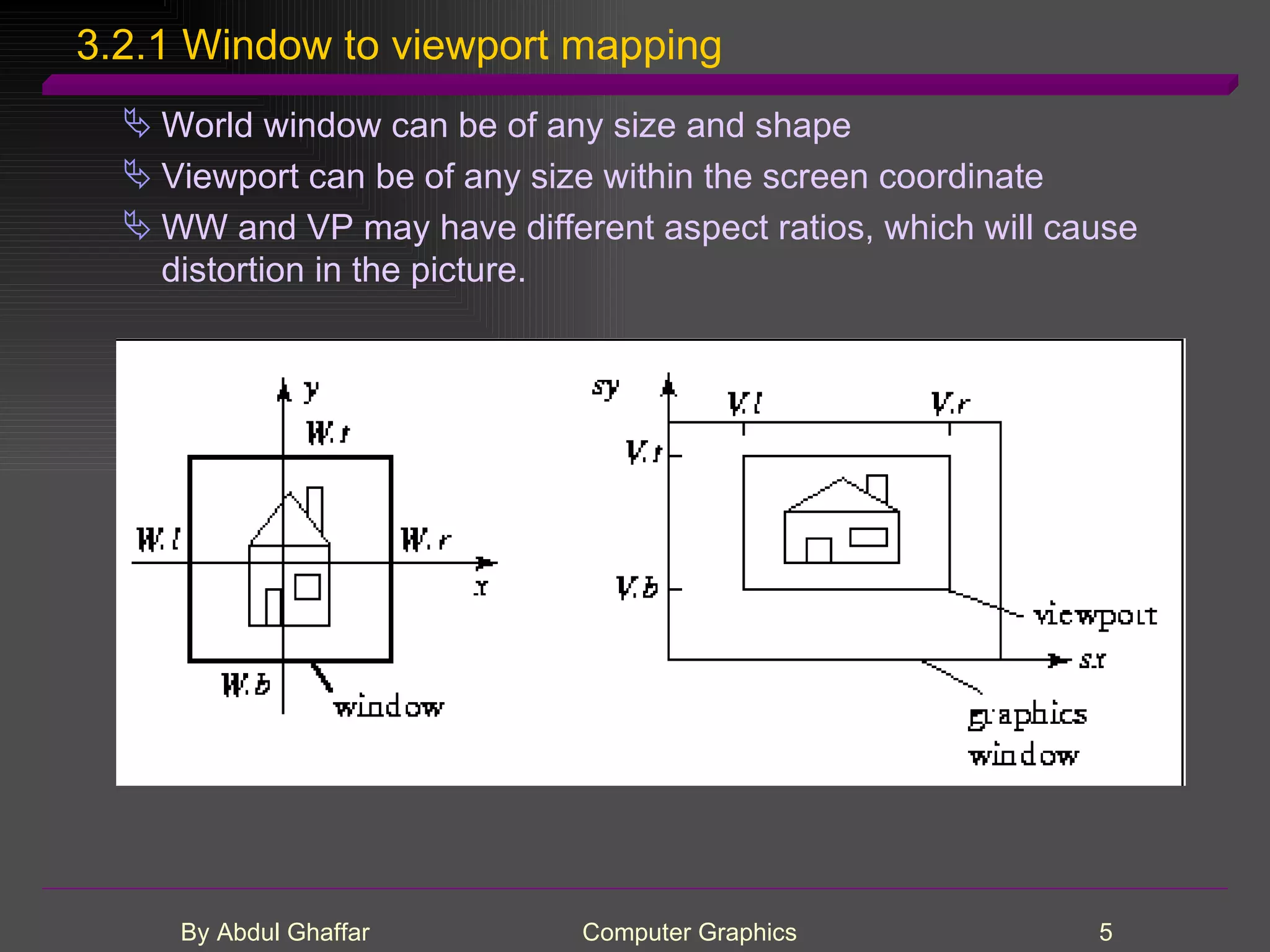
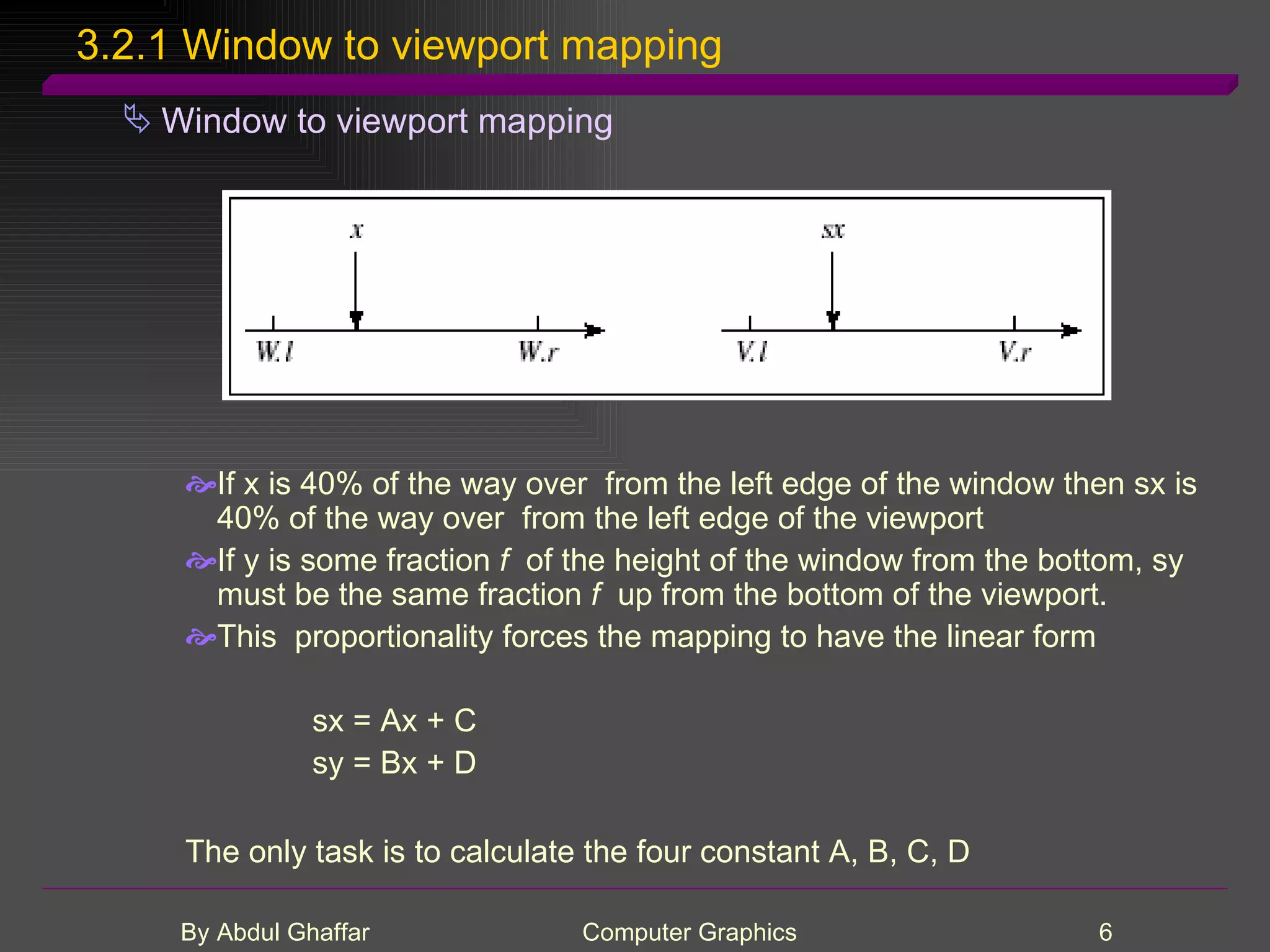
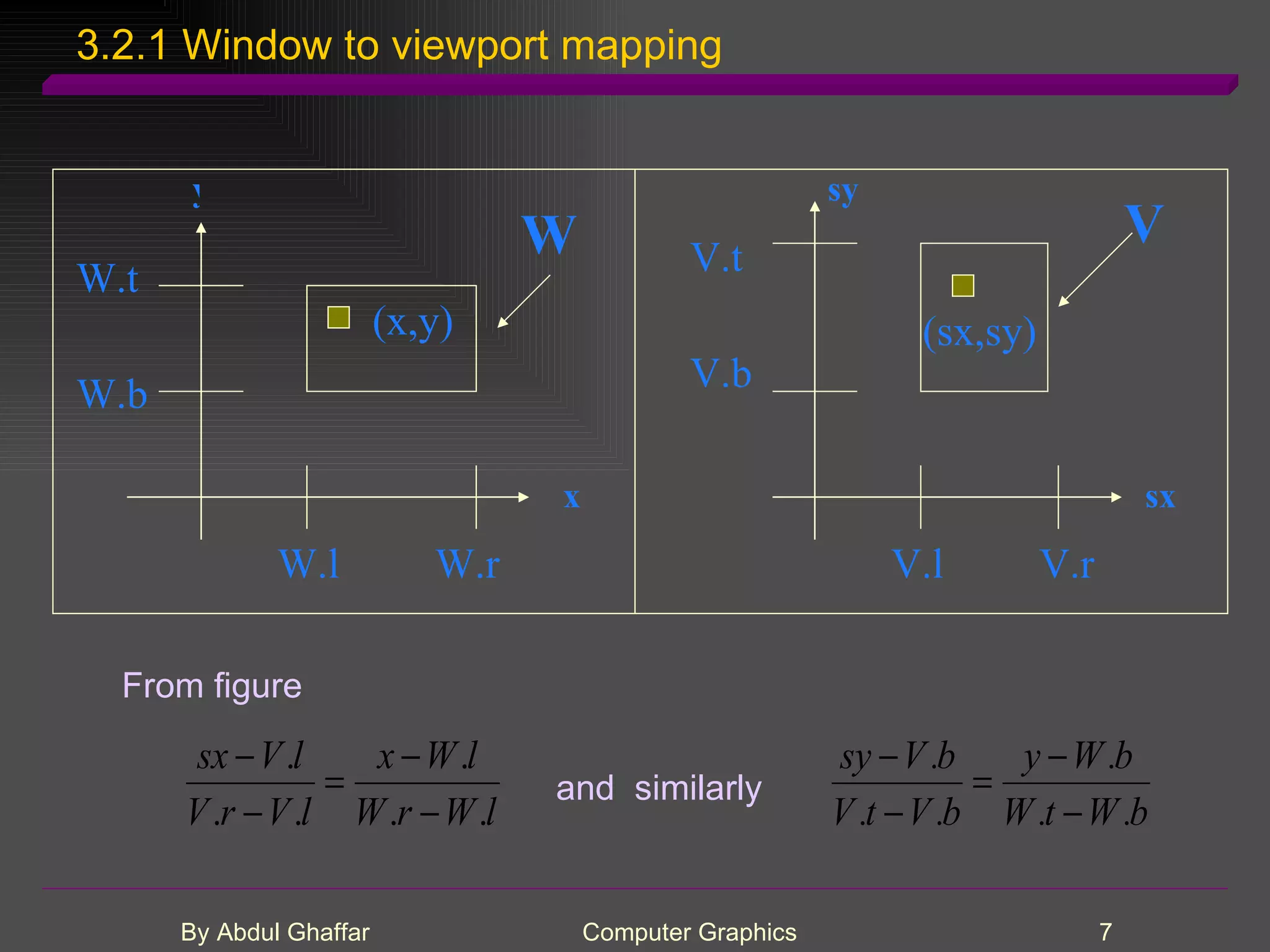
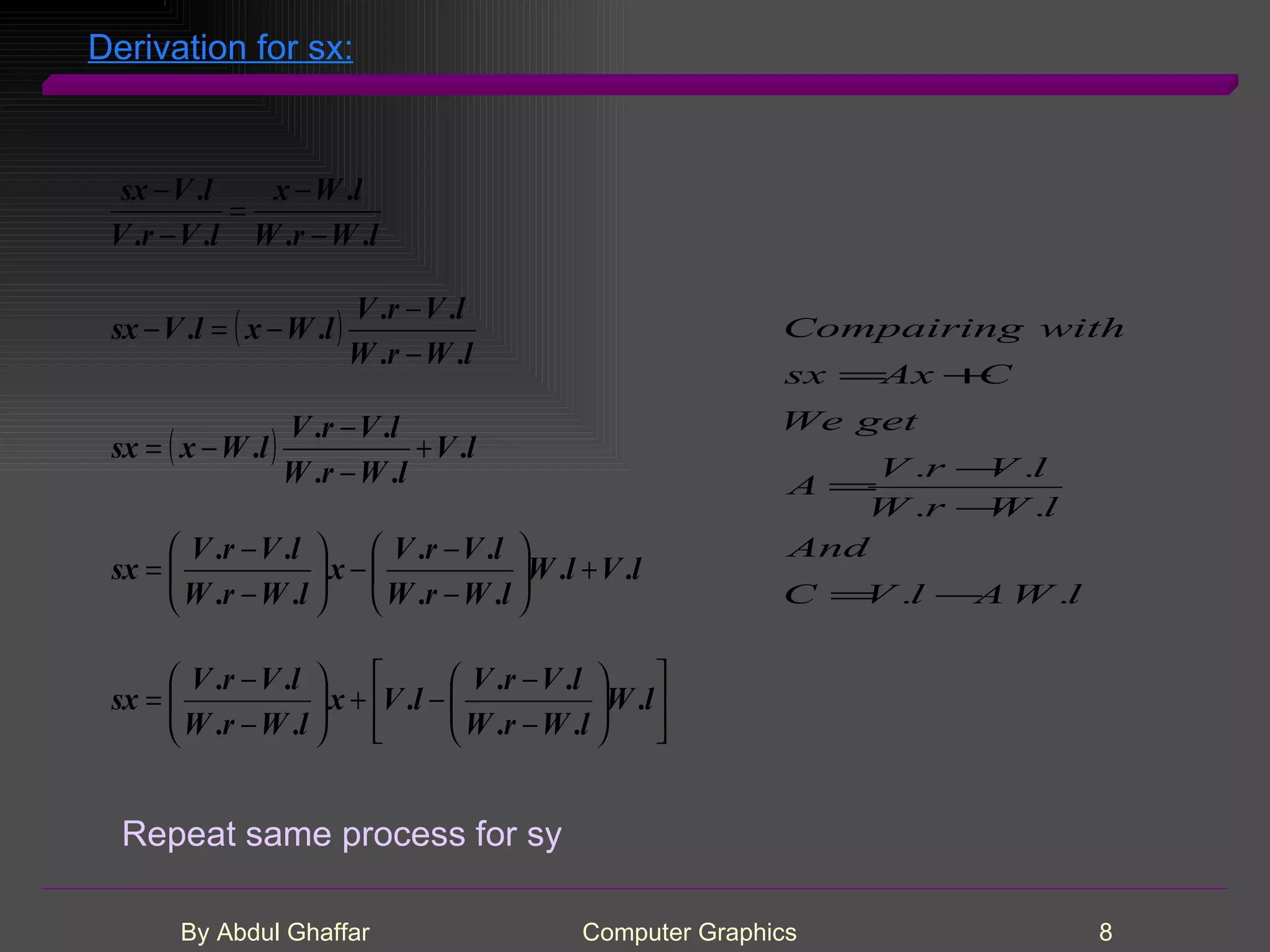
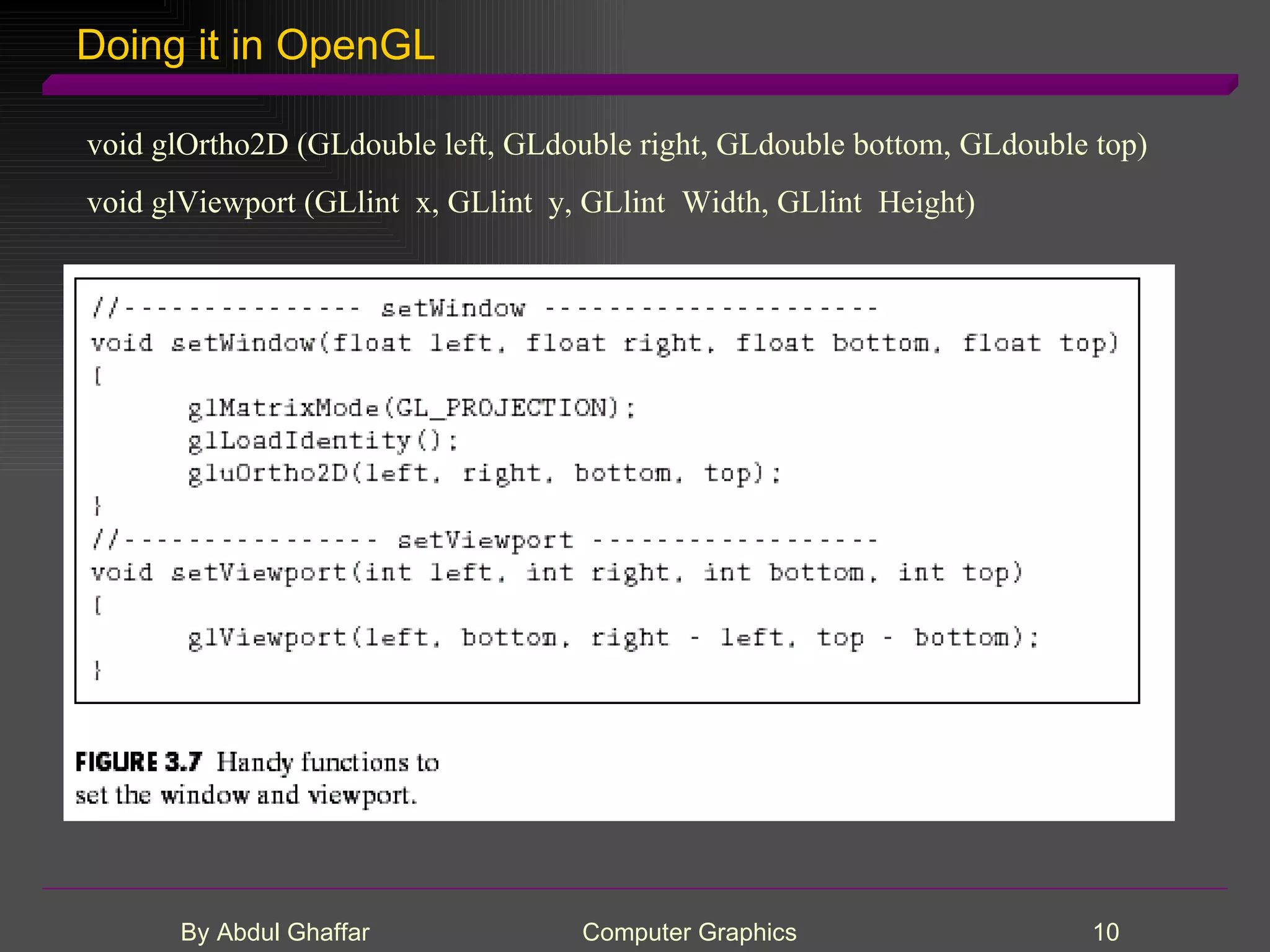
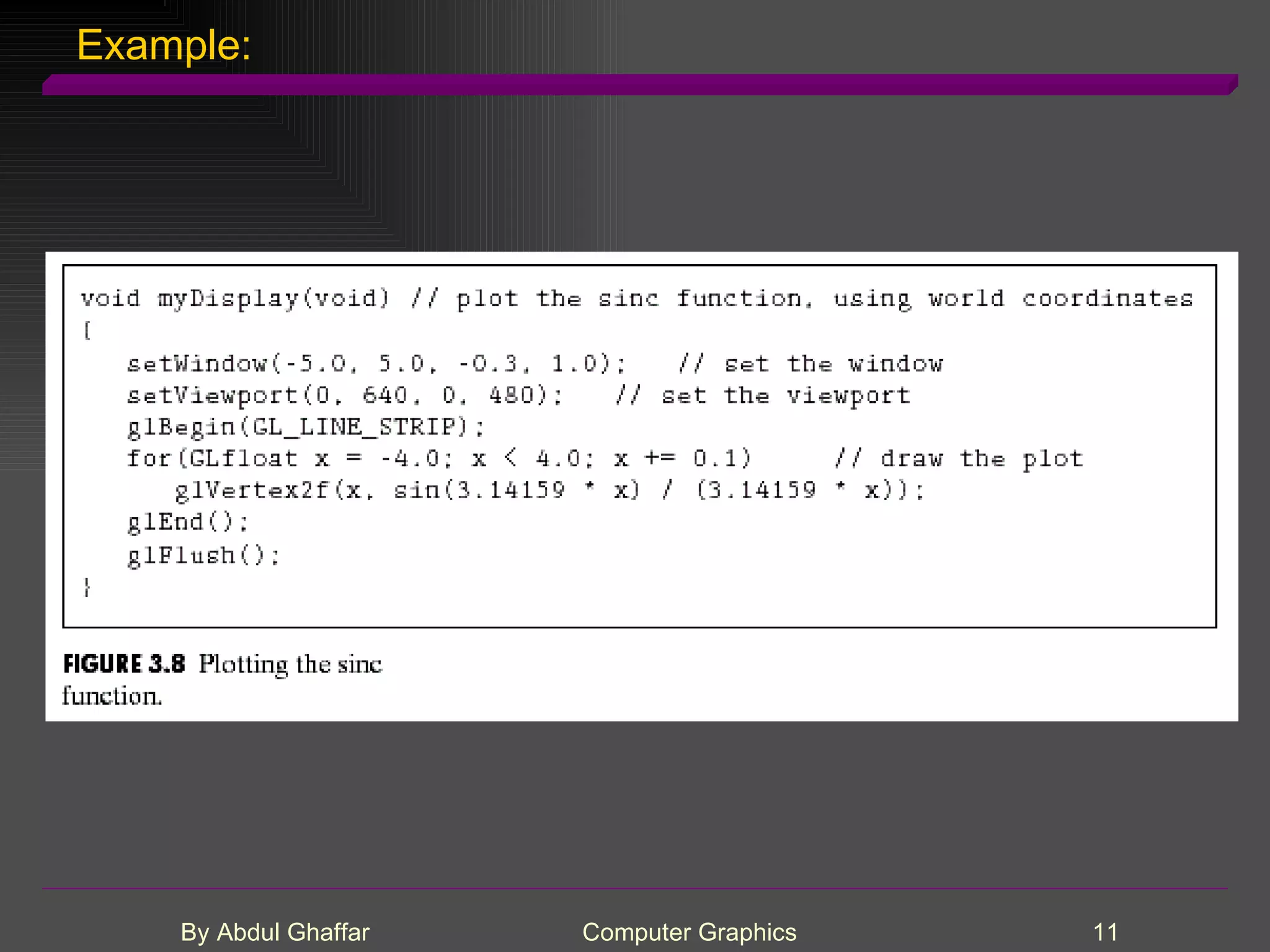
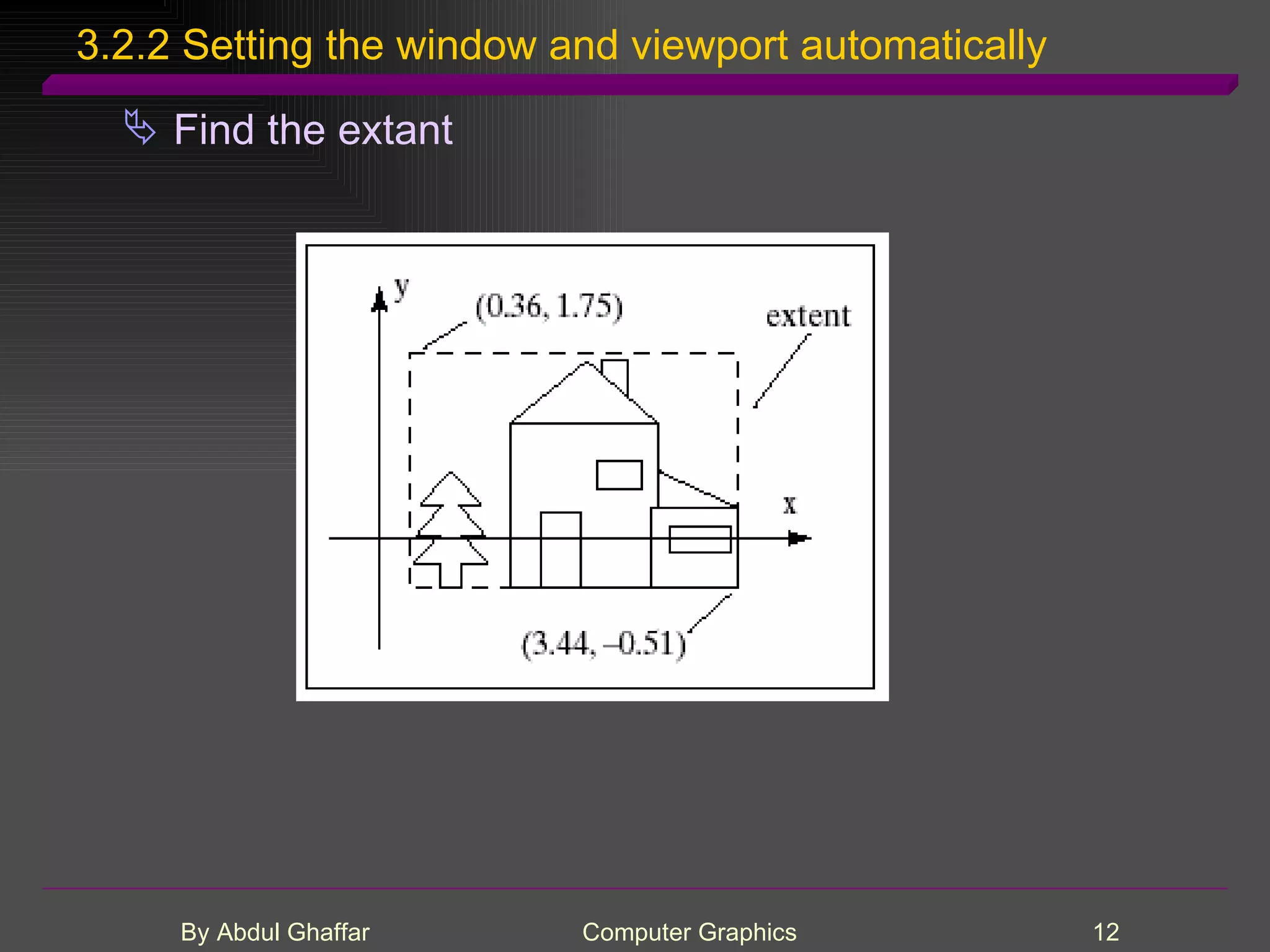
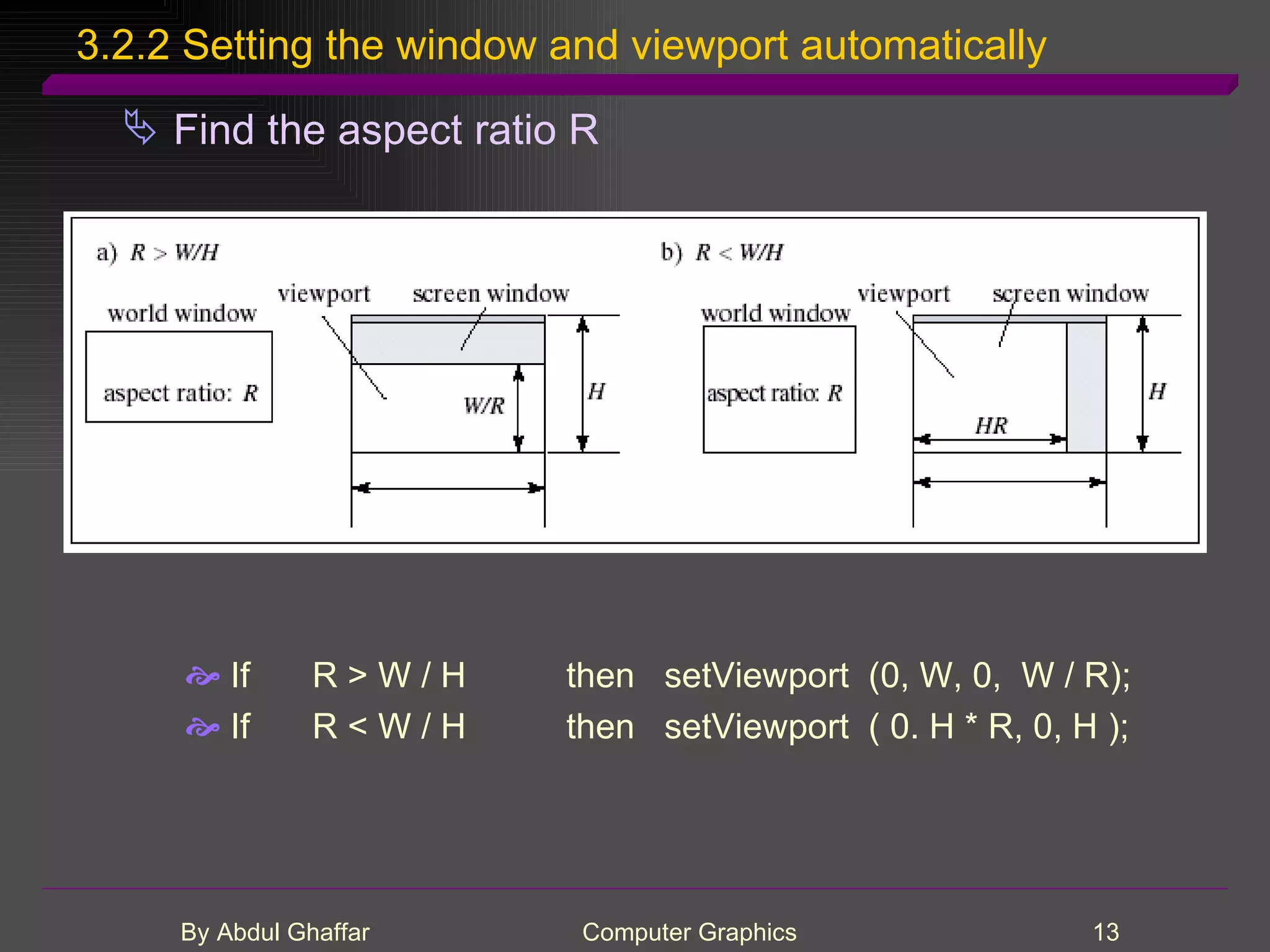
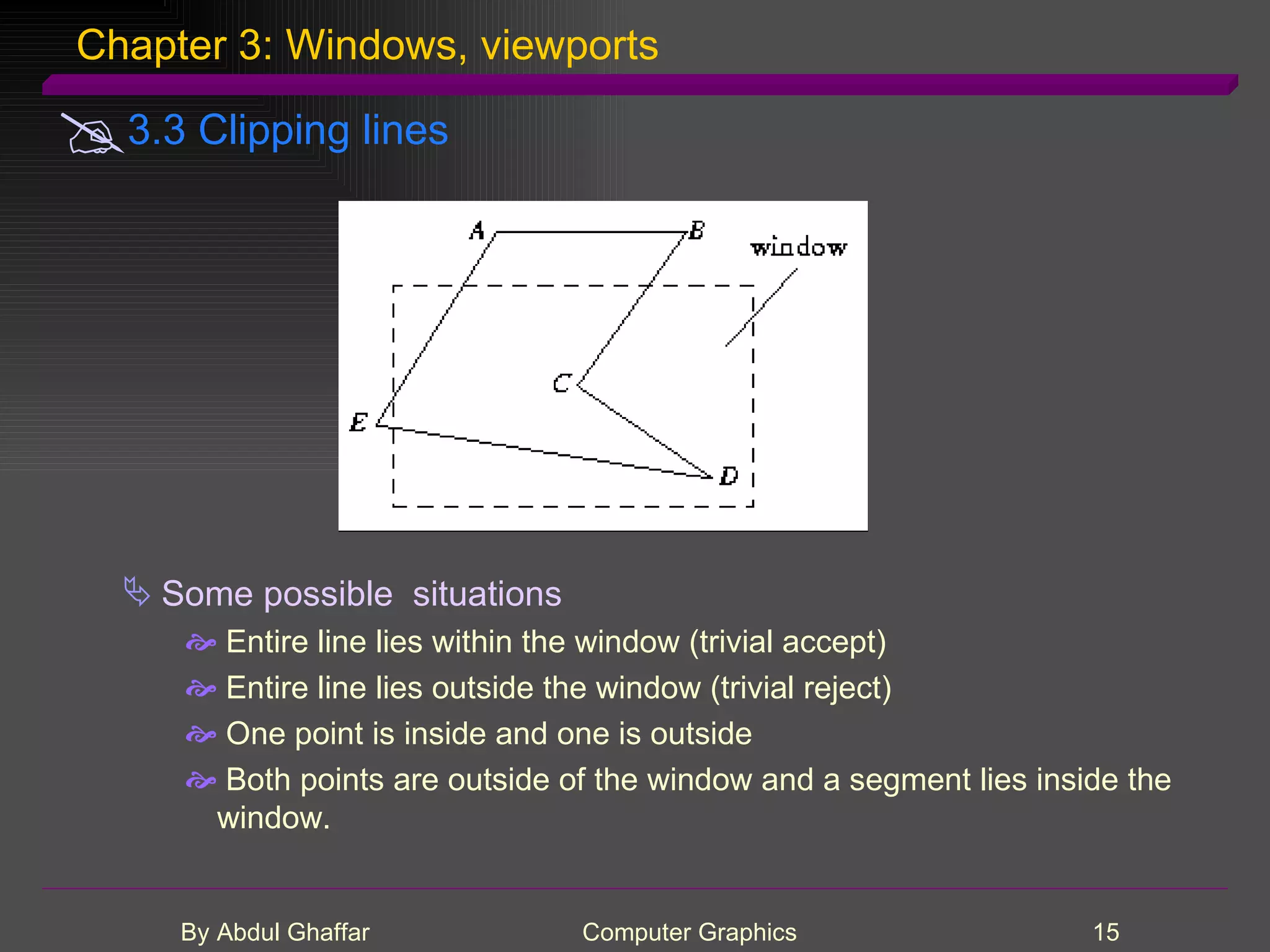
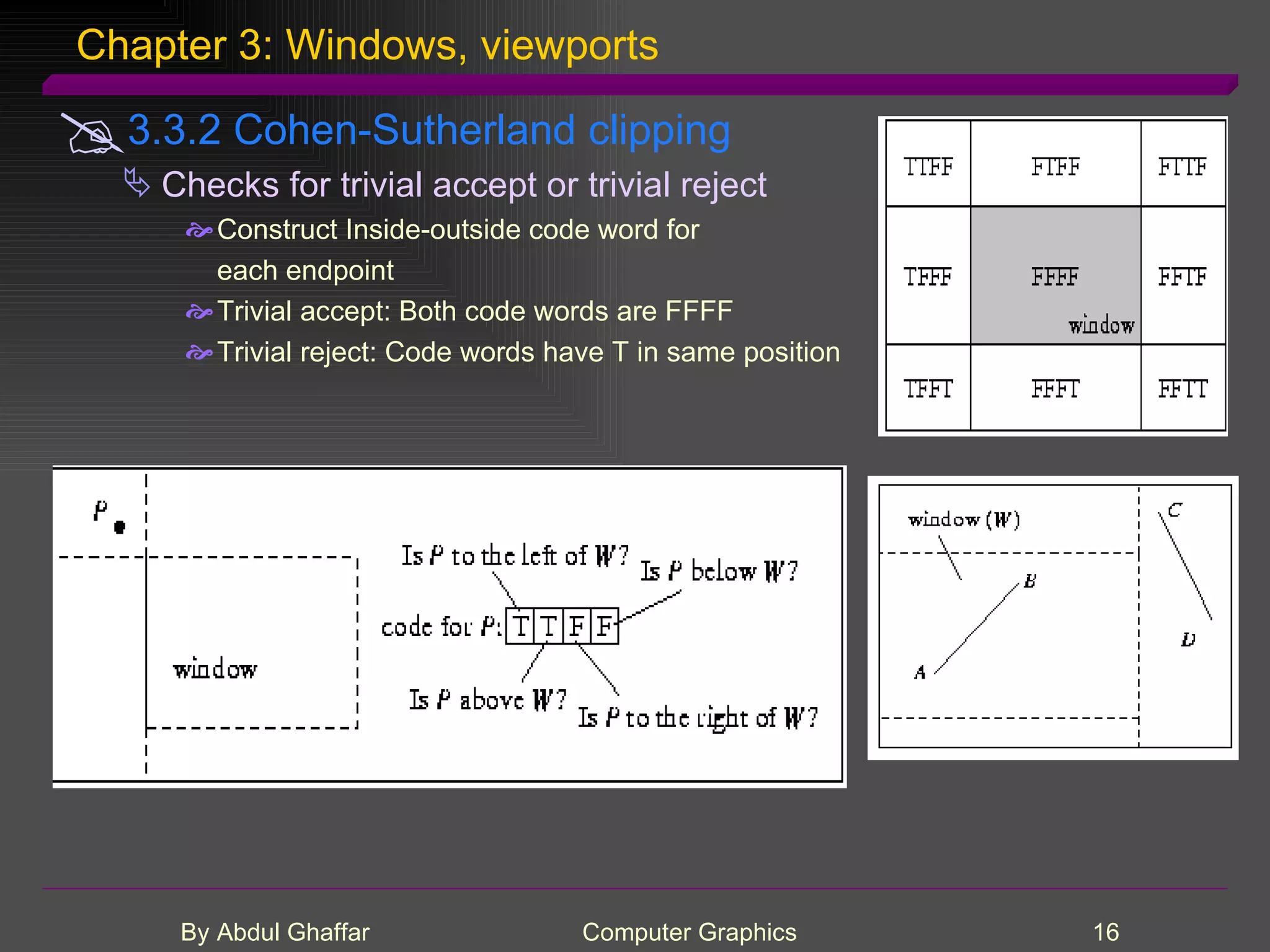
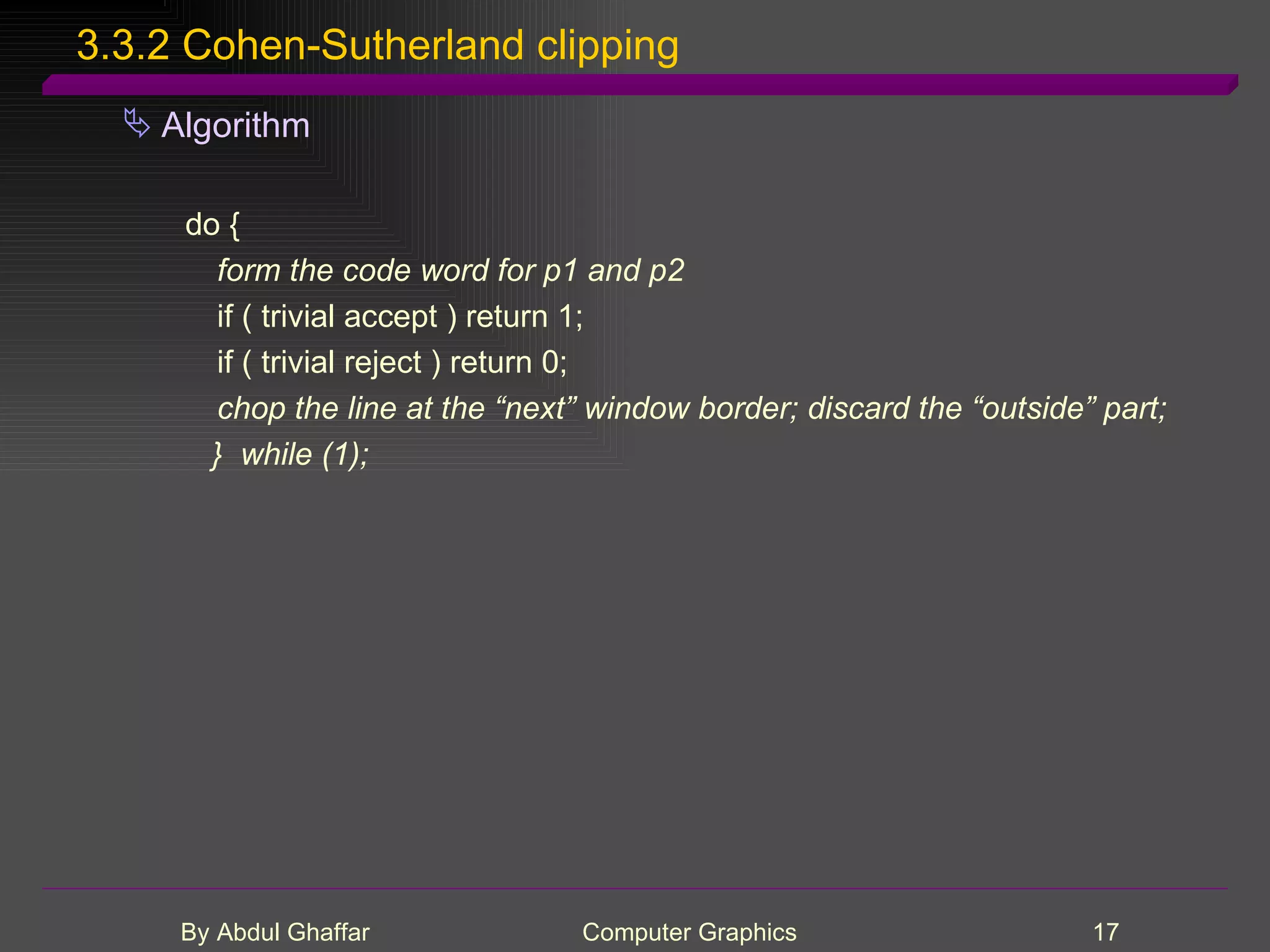
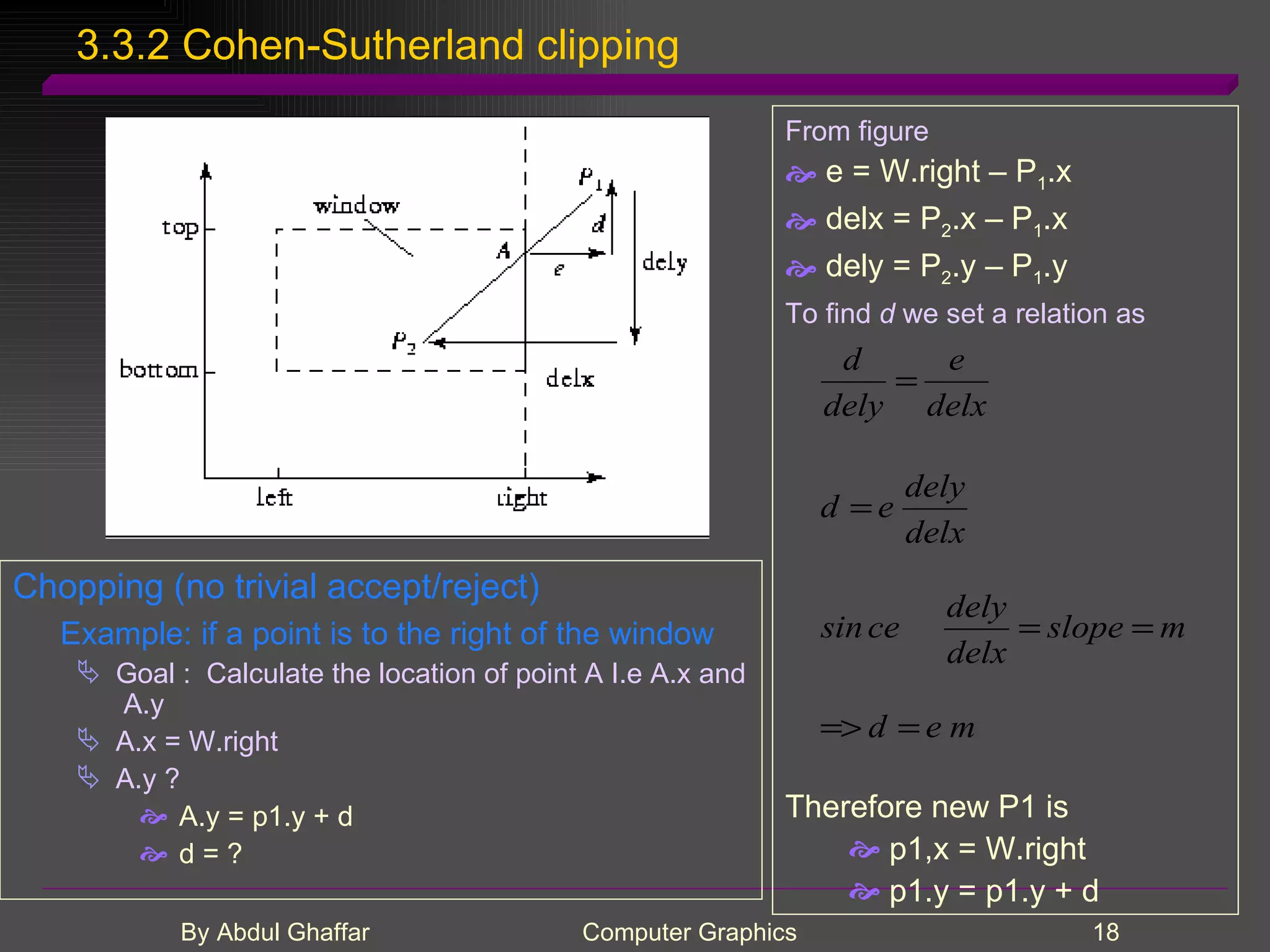
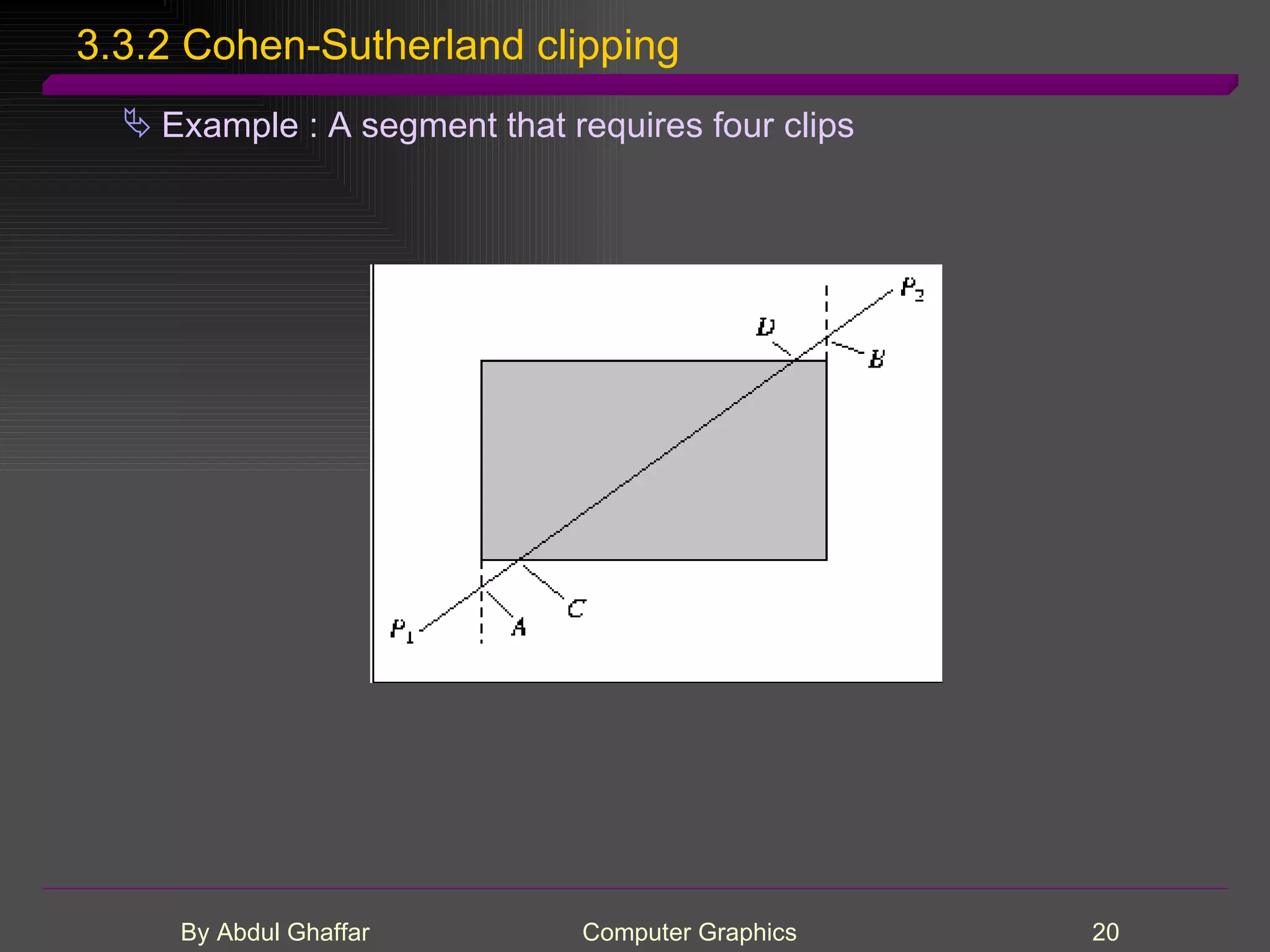
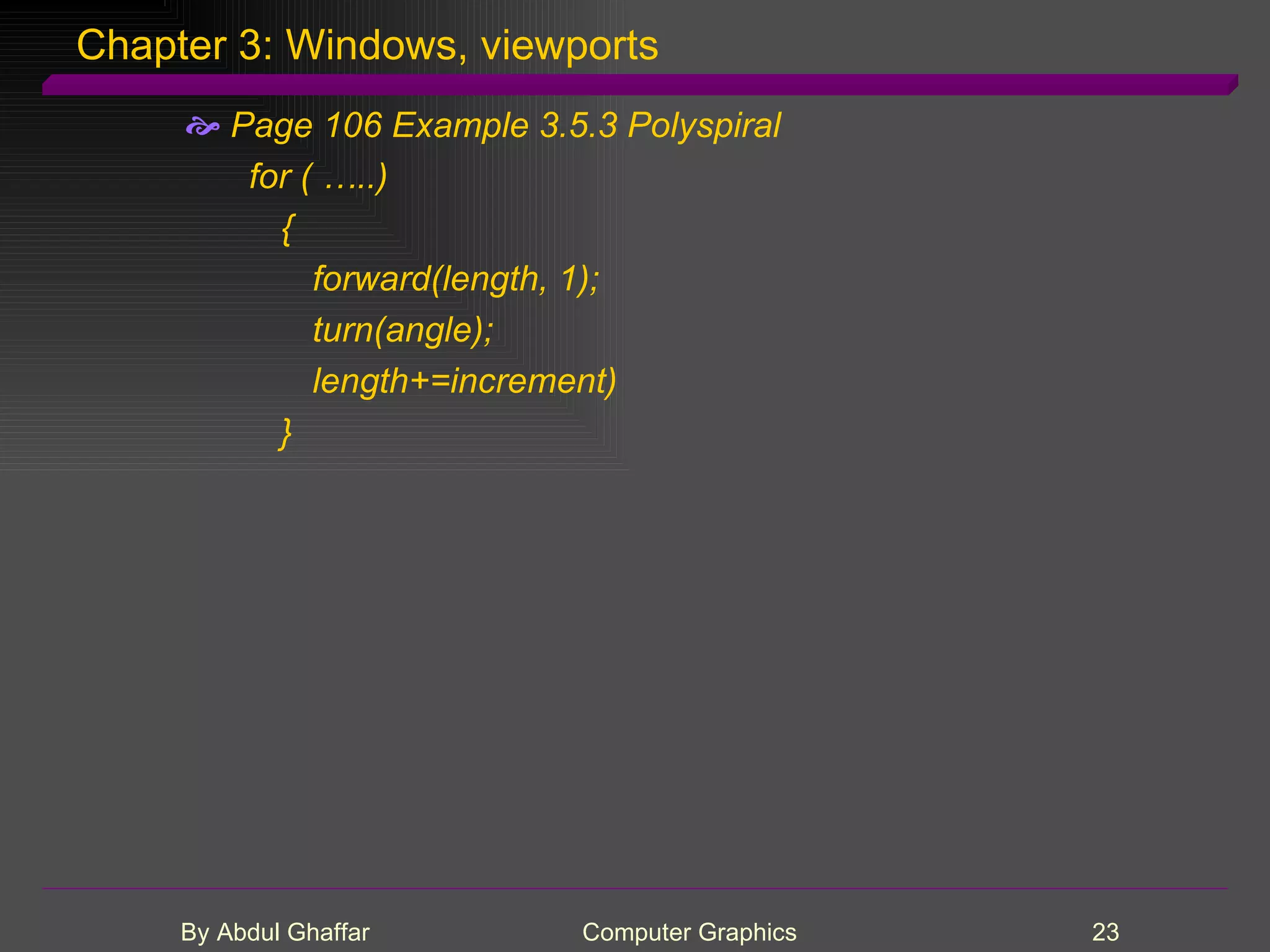
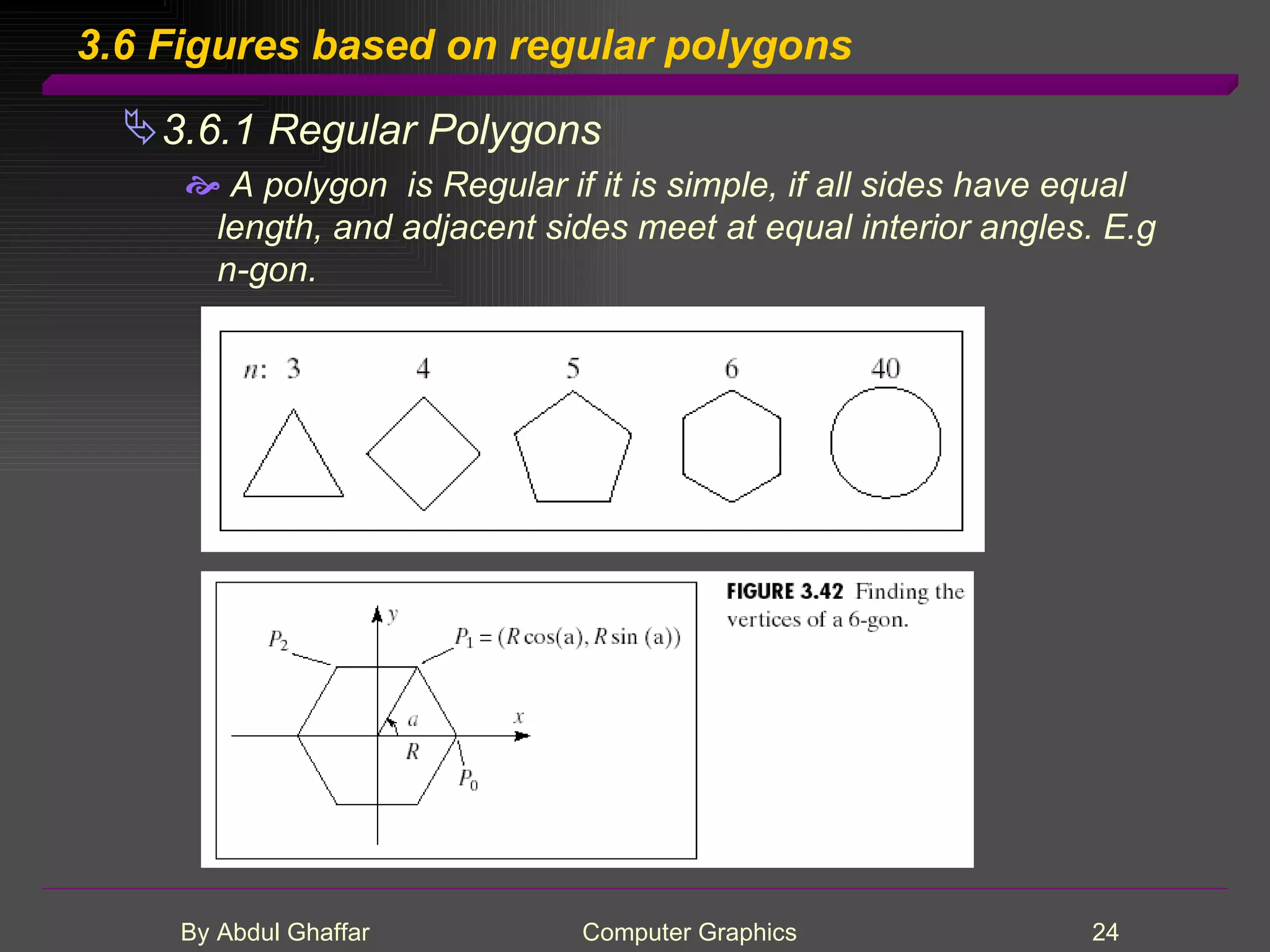
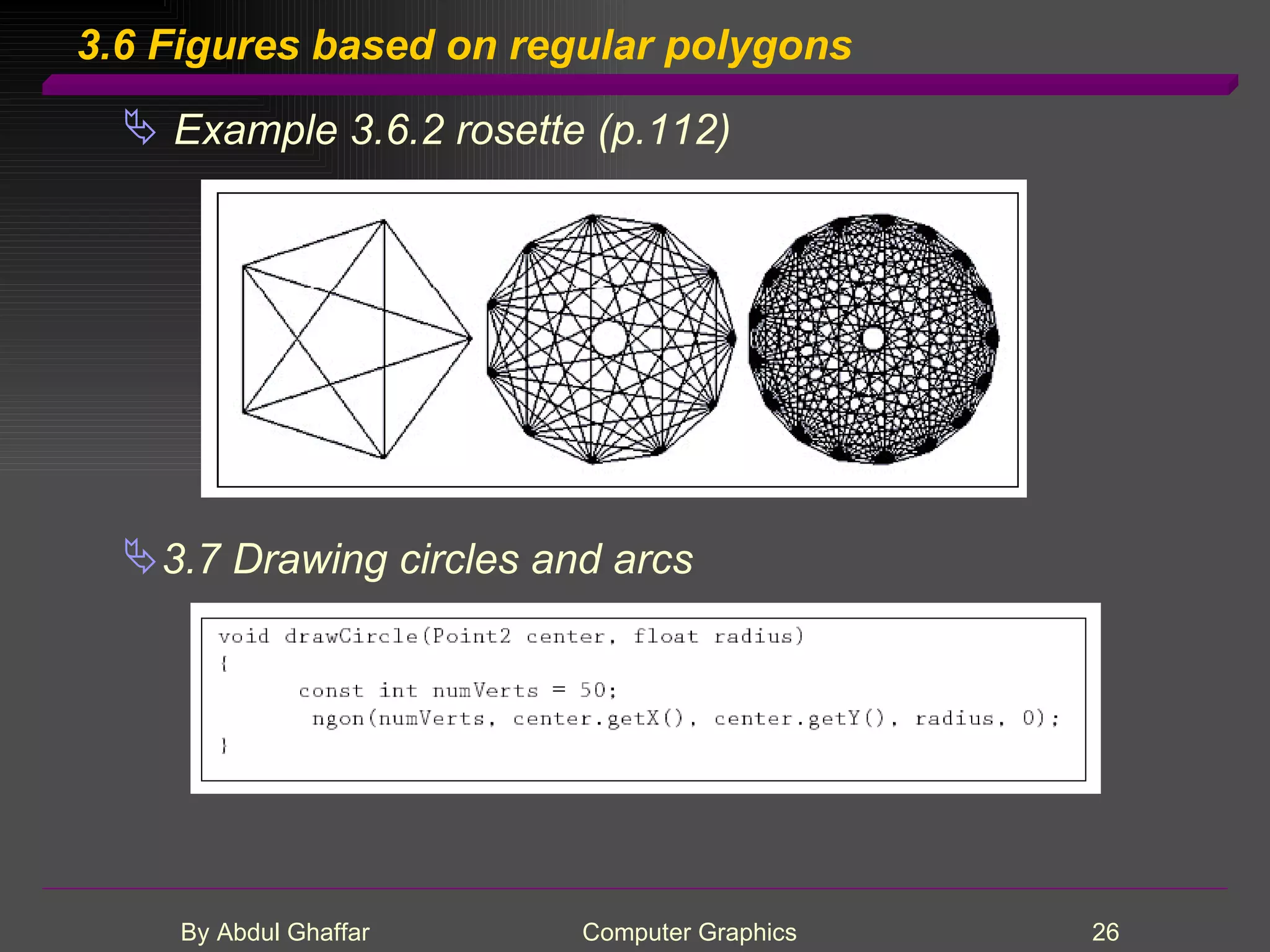
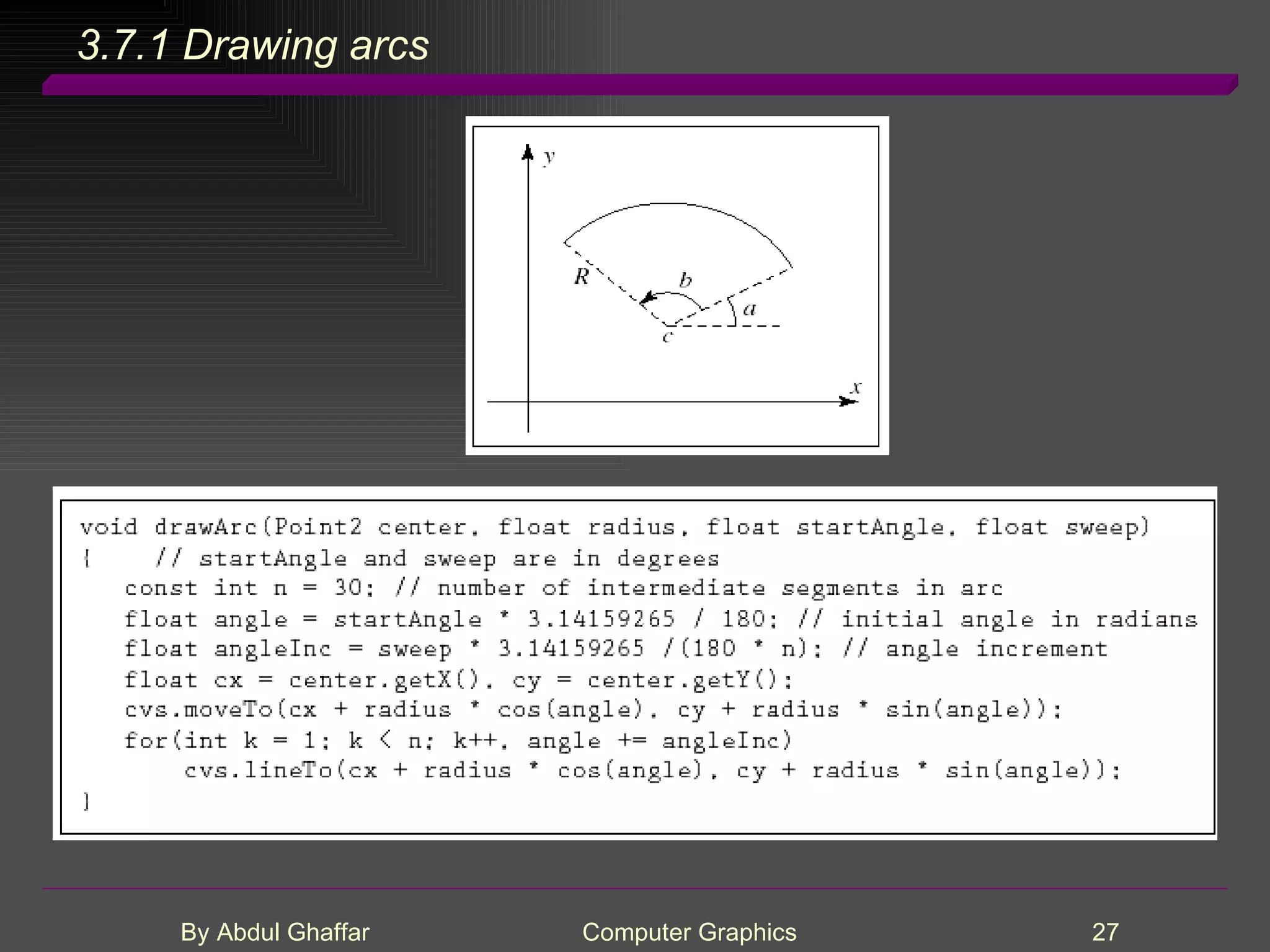
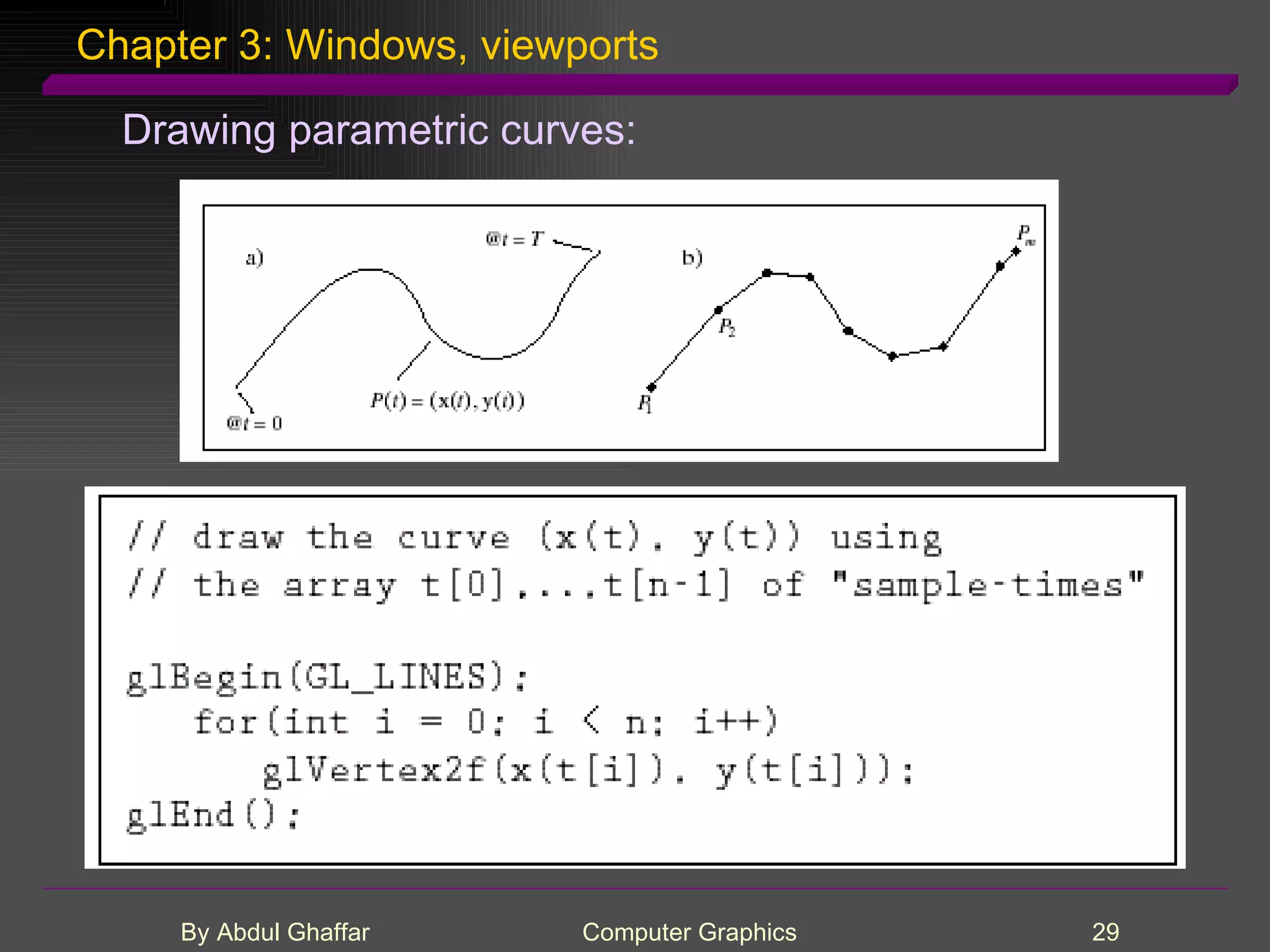
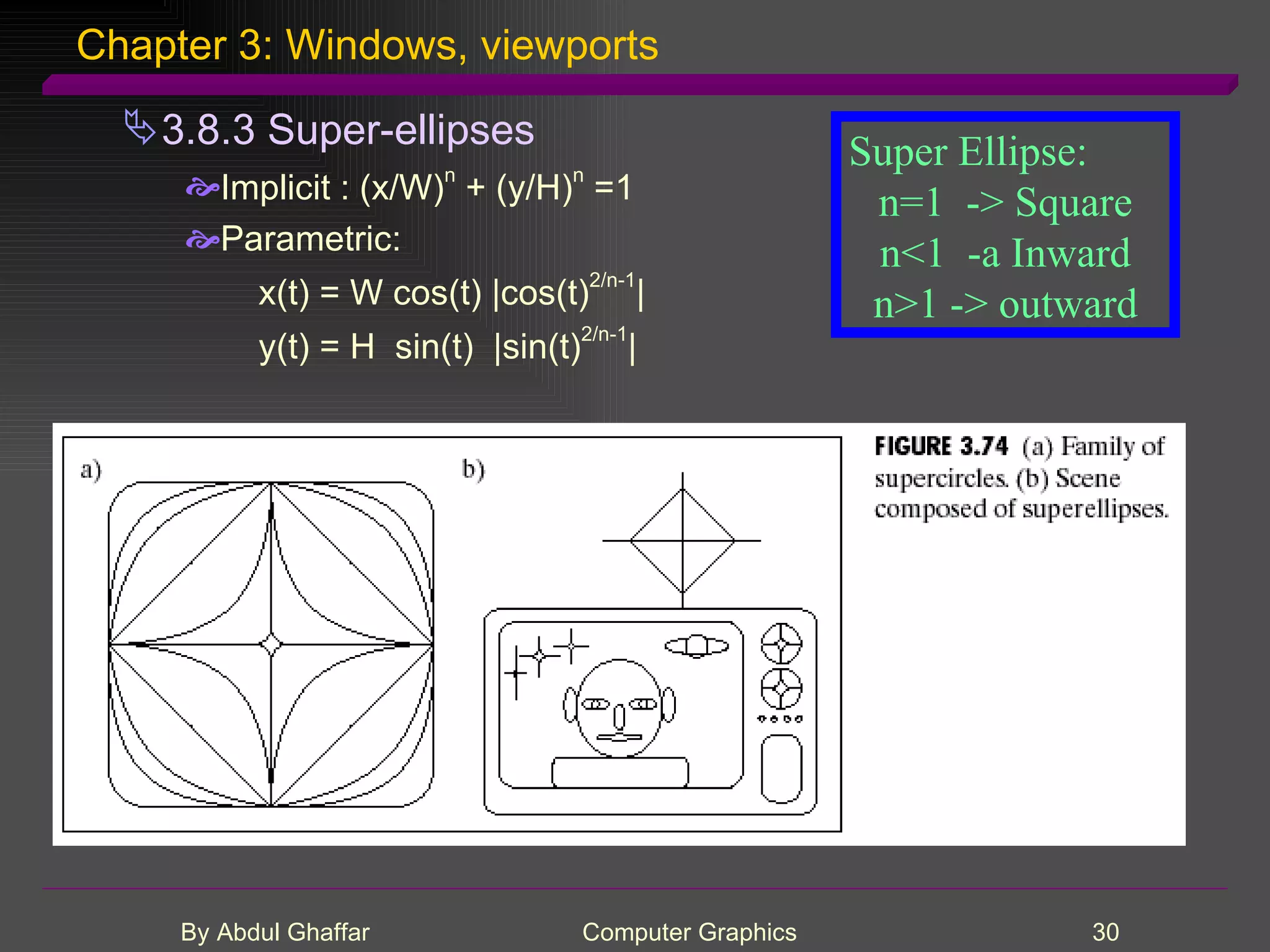
The document discusses various concepts related to drawing in computer graphics such as world coordinates, windows, viewports, window-viewport mapping, clipping lines, regular polygons, circles, arcs, parametric and polar curves. It provides details on setting the window and viewport, Cohen-Sutherland line clipping algorithm, drawing figures based on regular polygons, parametric representations of lines, ellipses and superellipses. It also describes the canvas class for drawing and examples of drawing polygons, spirals, rosettes and other shapes.