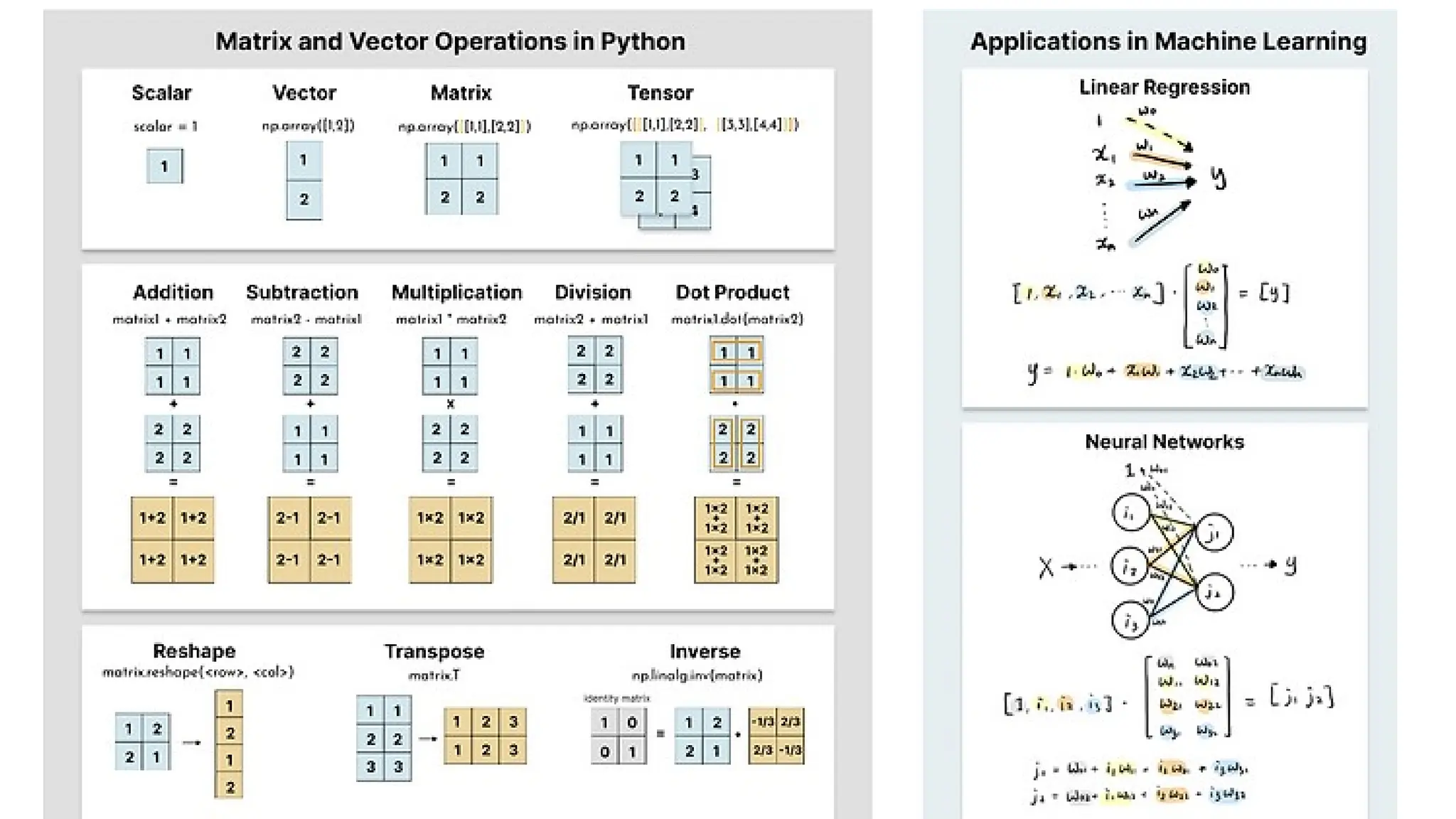
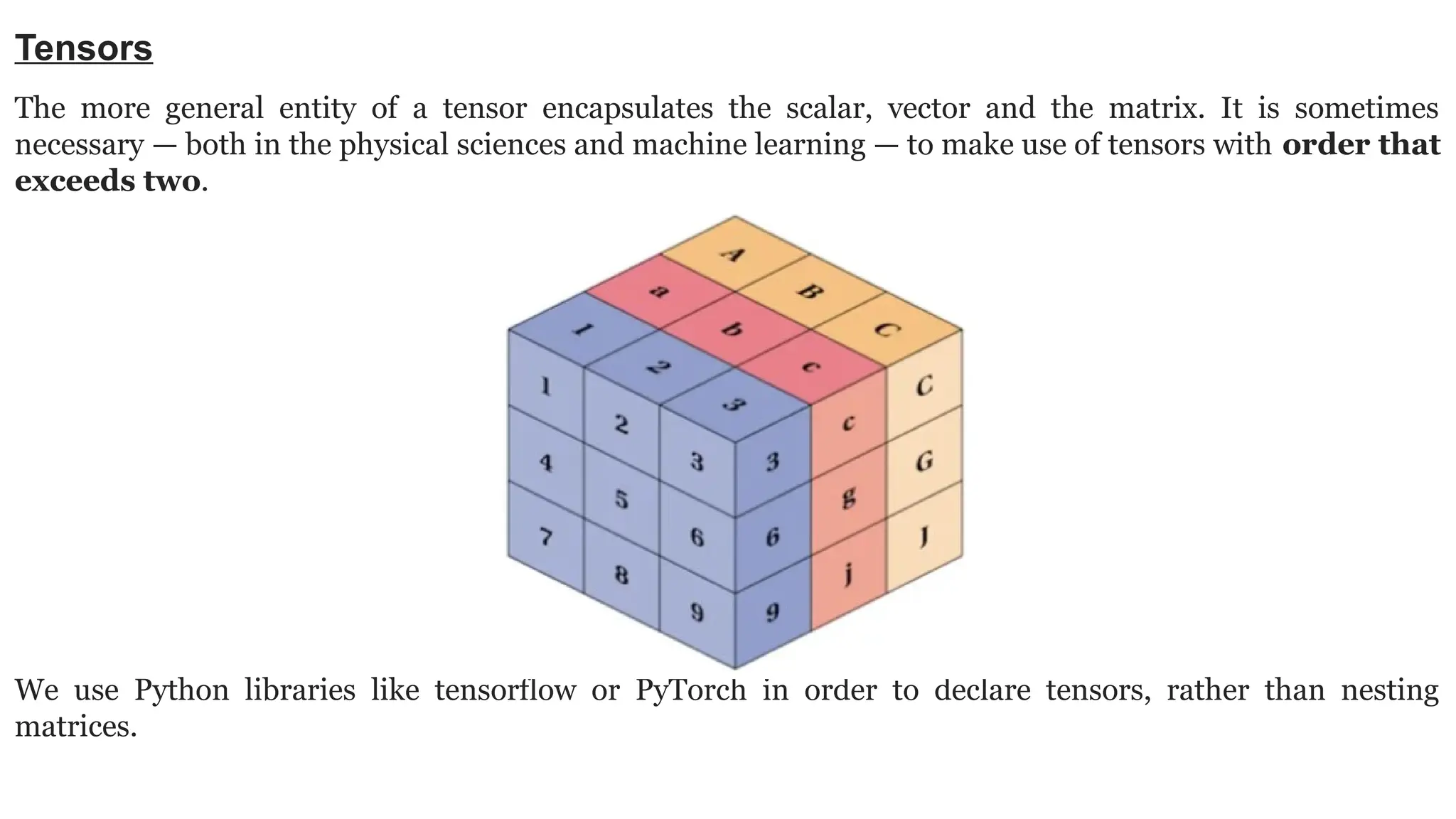
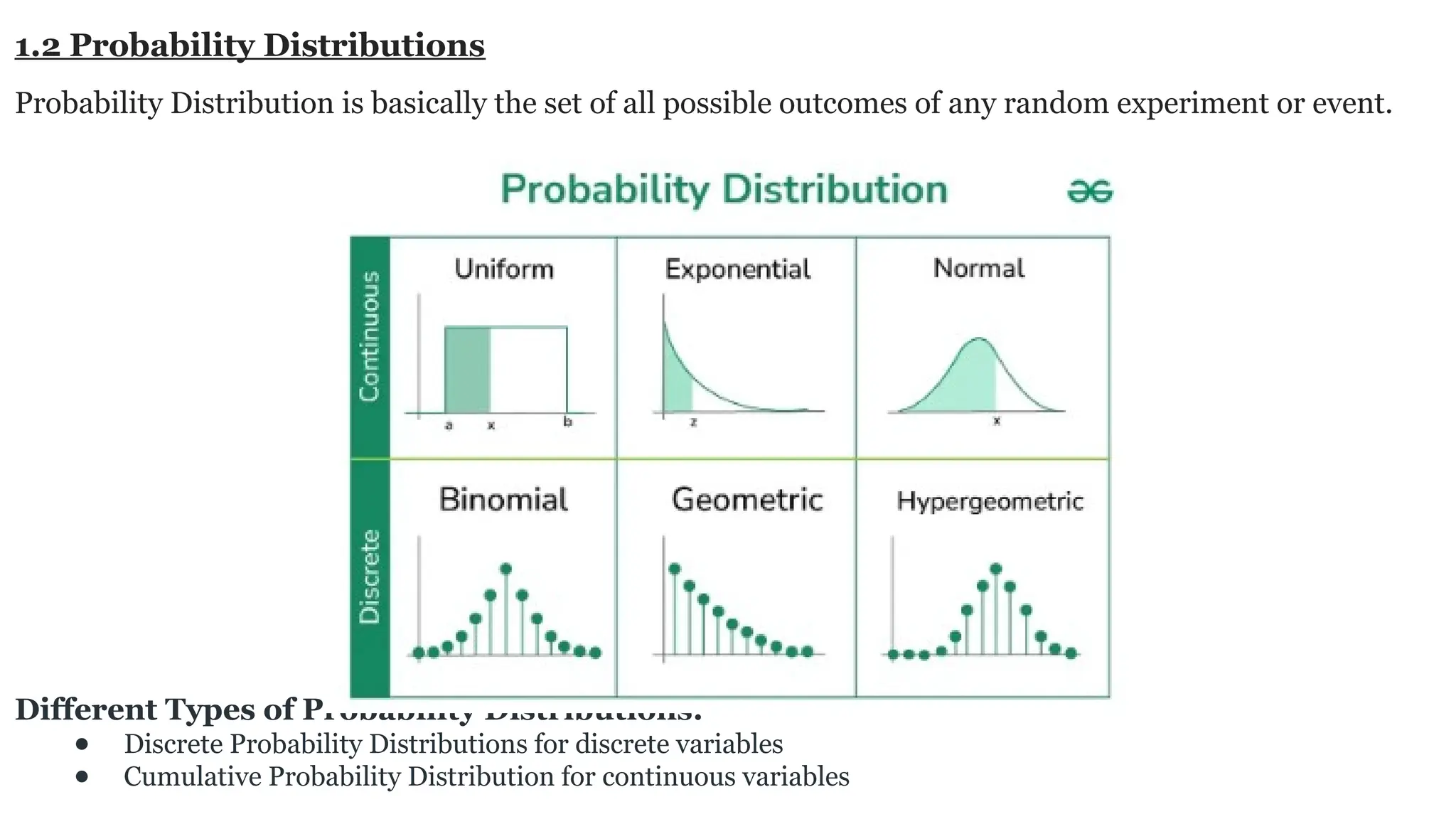
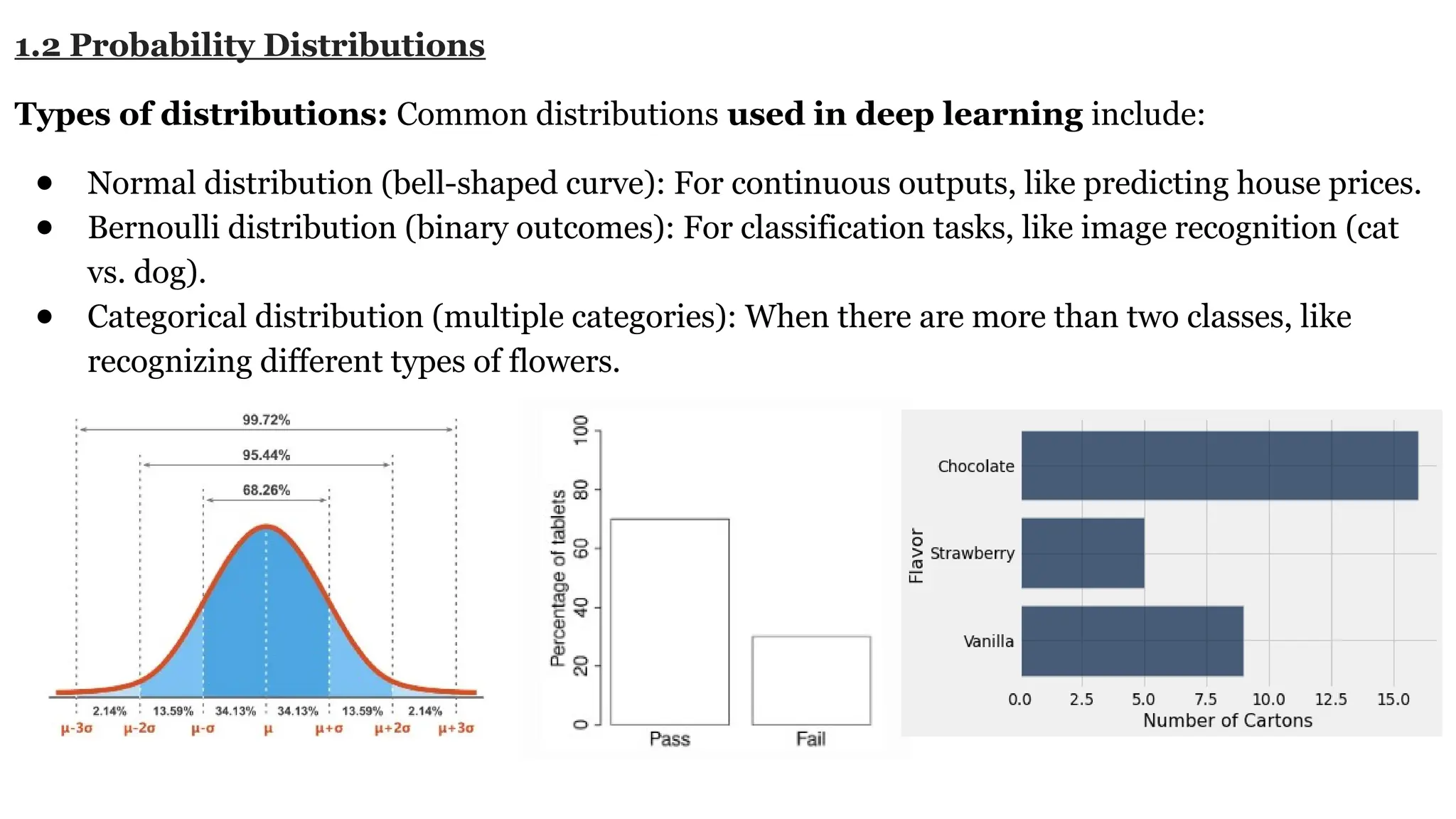
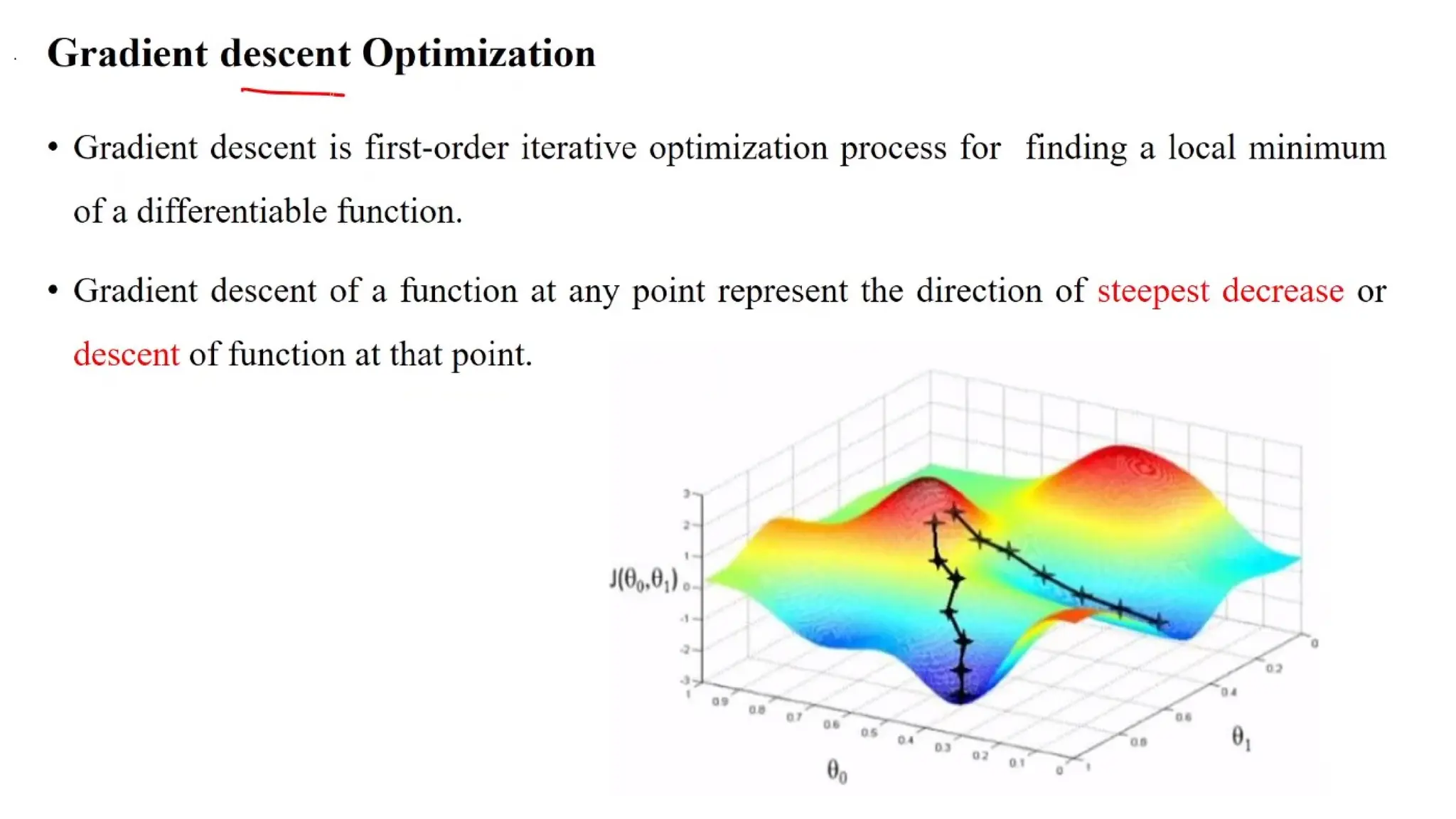
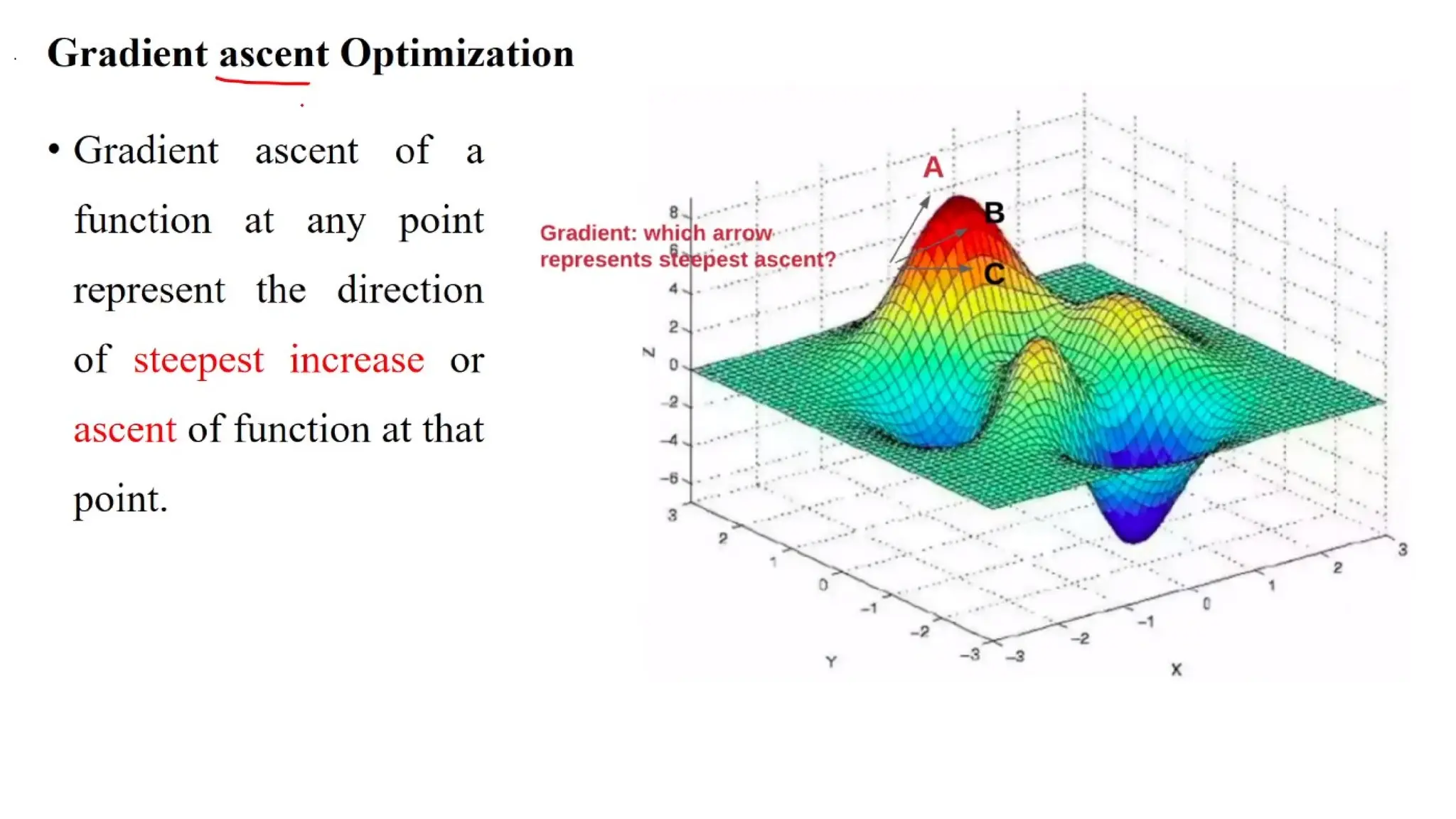
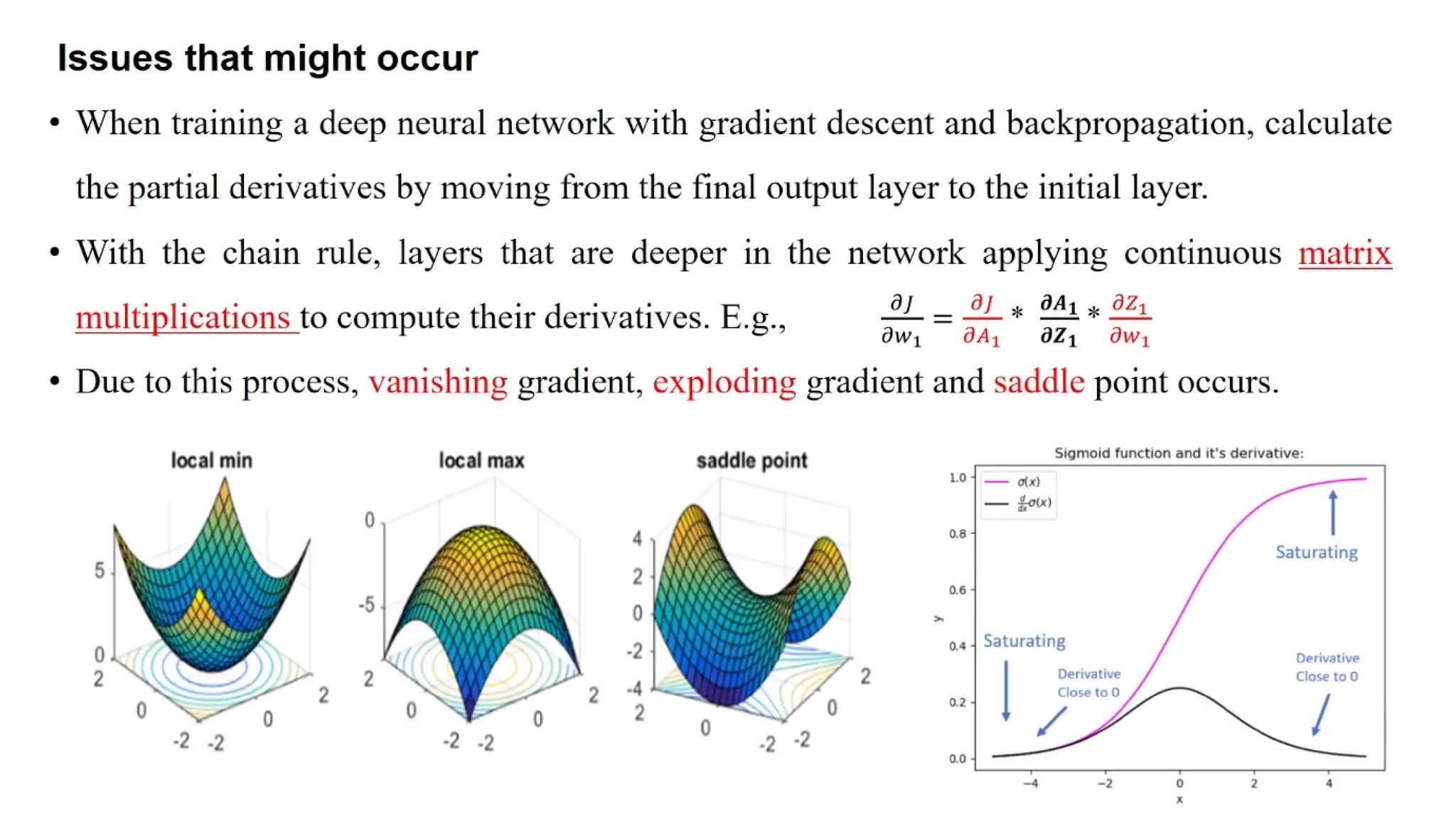
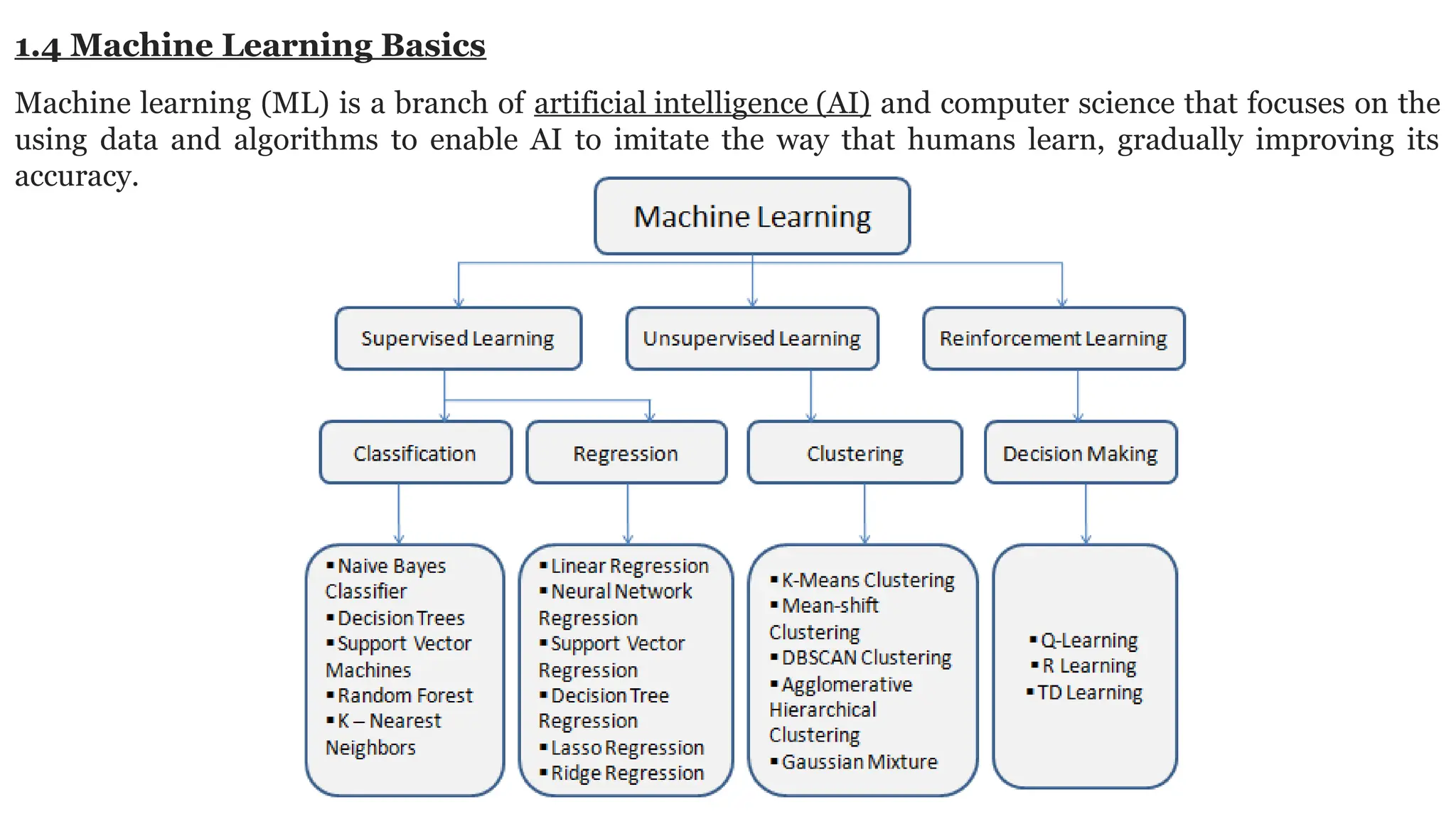
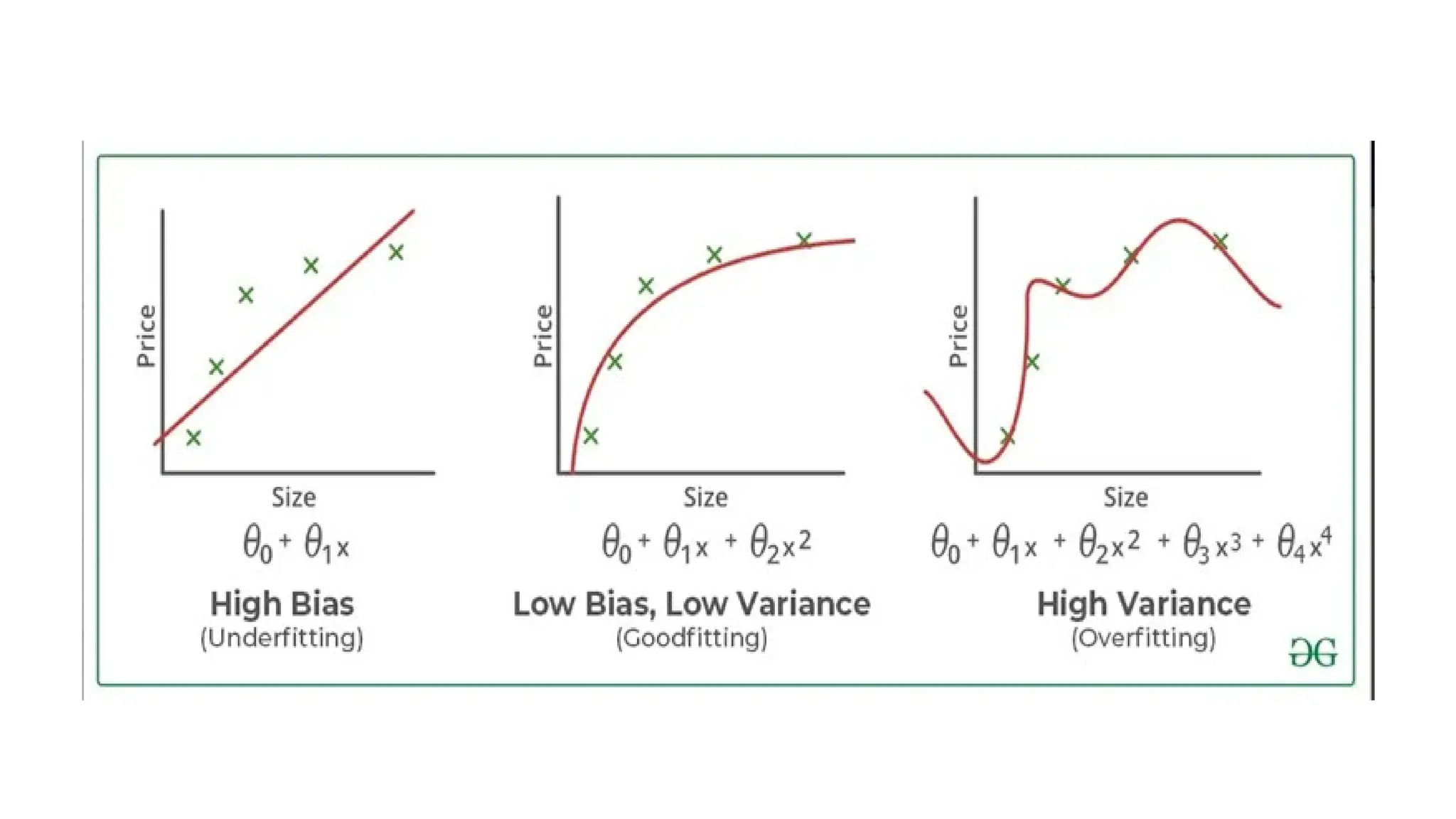
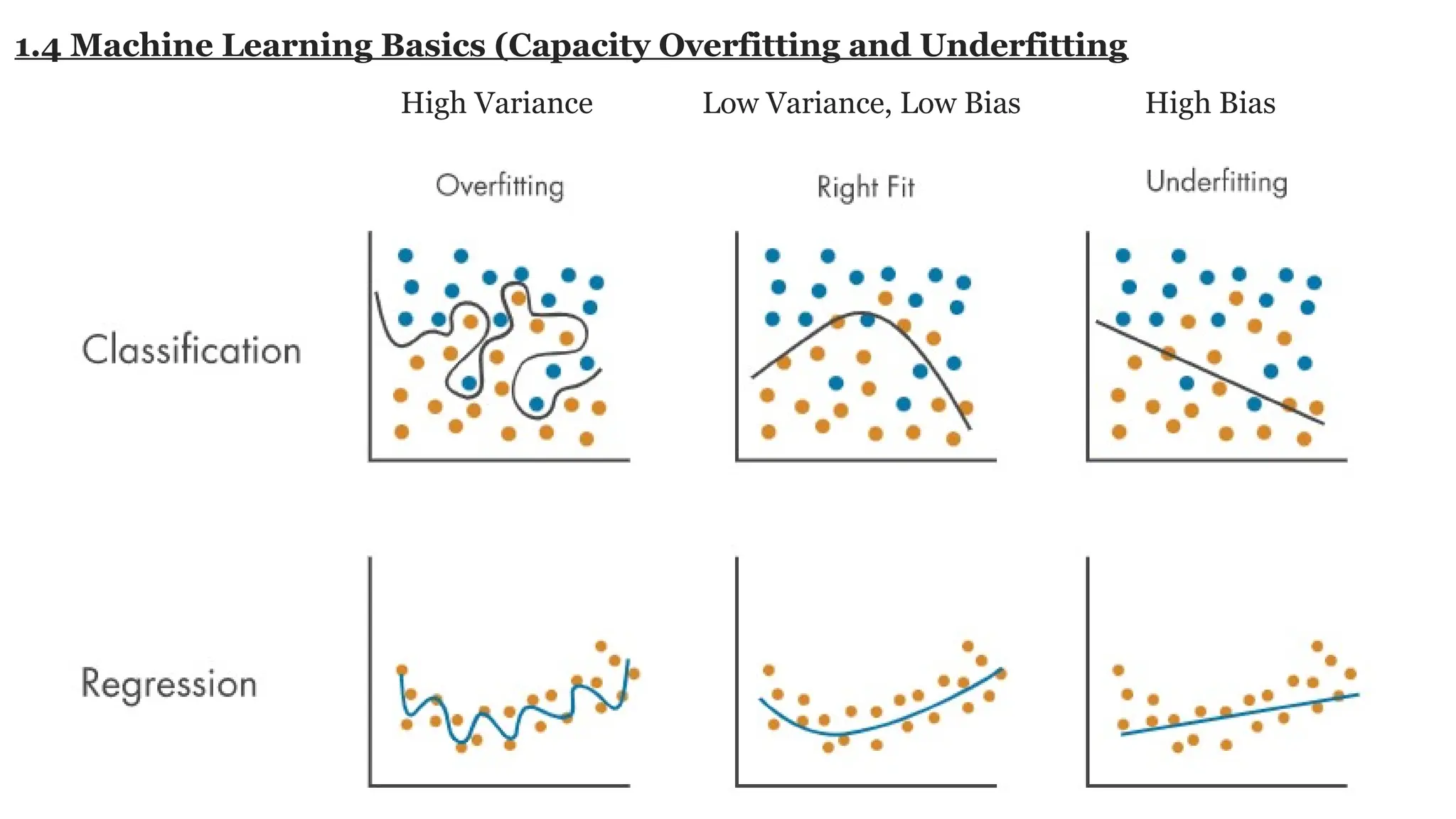
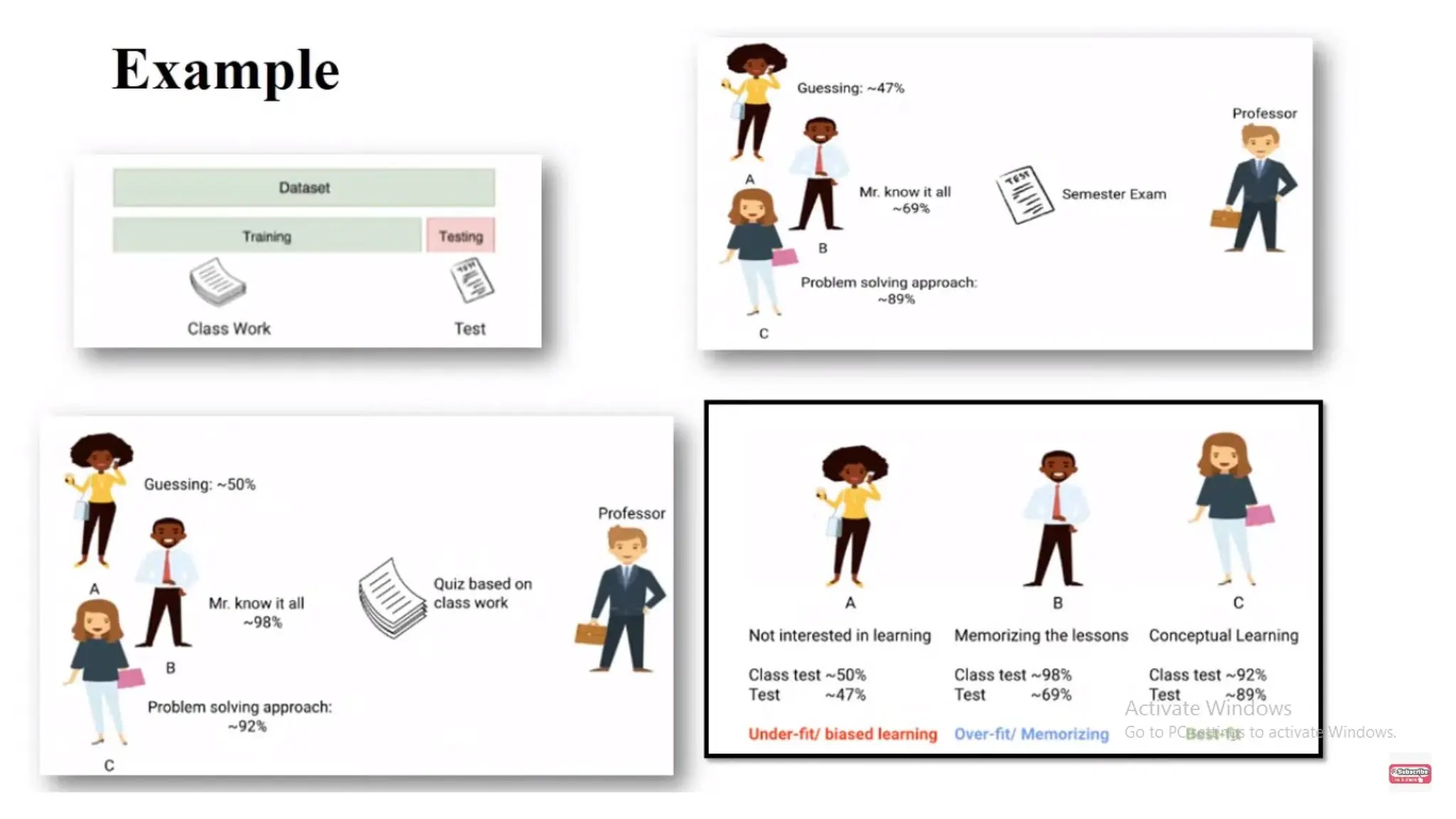
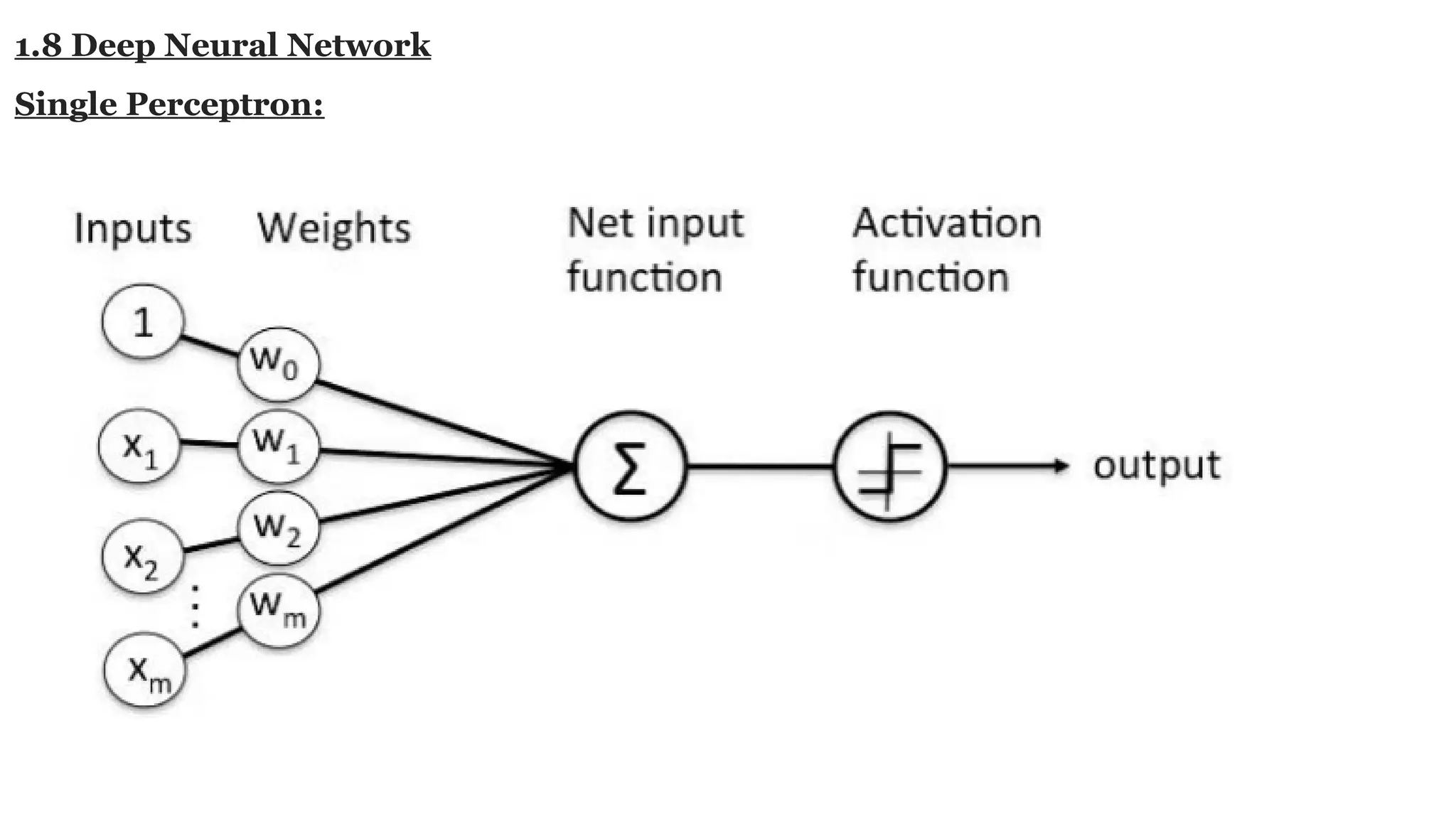
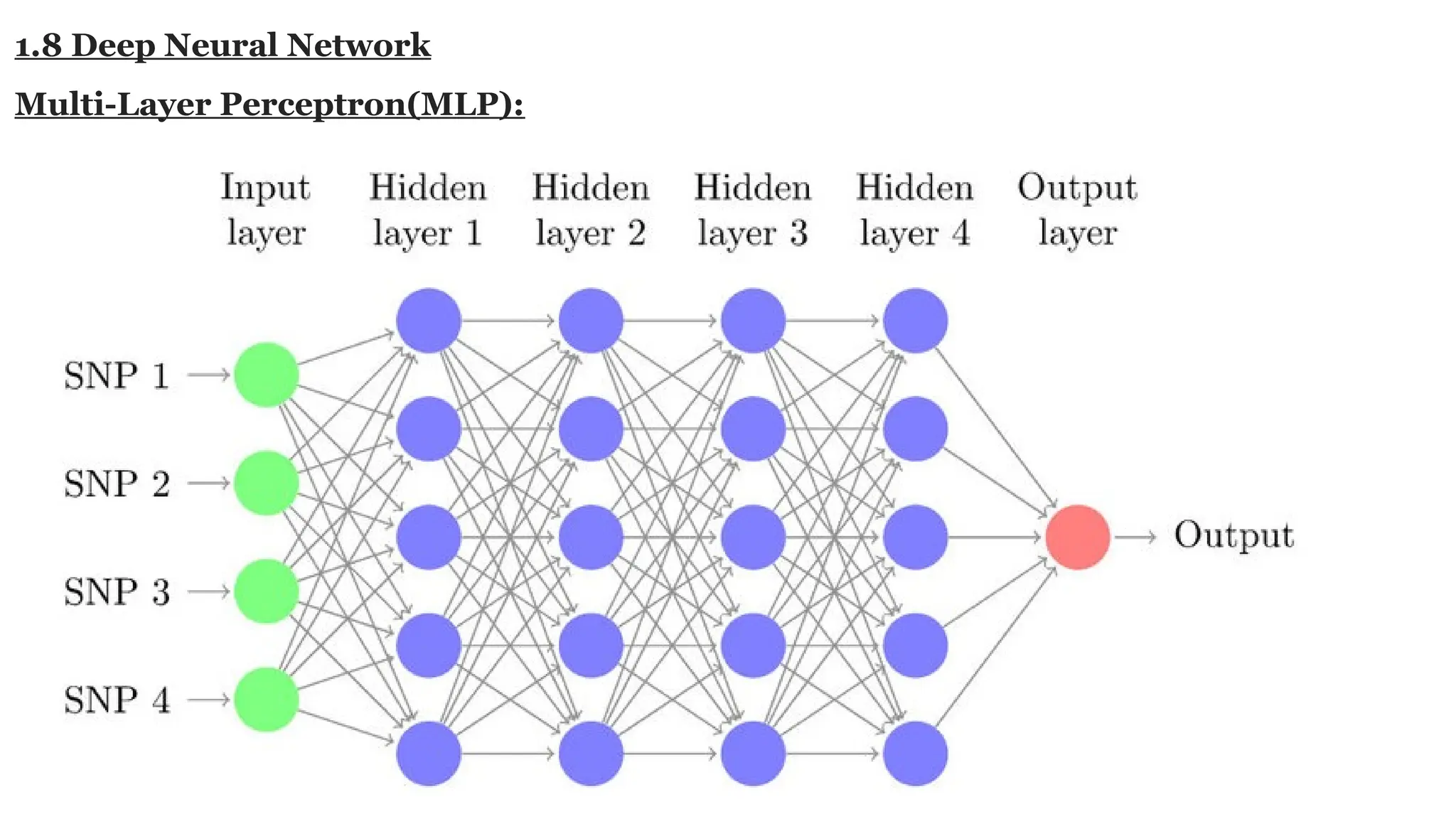
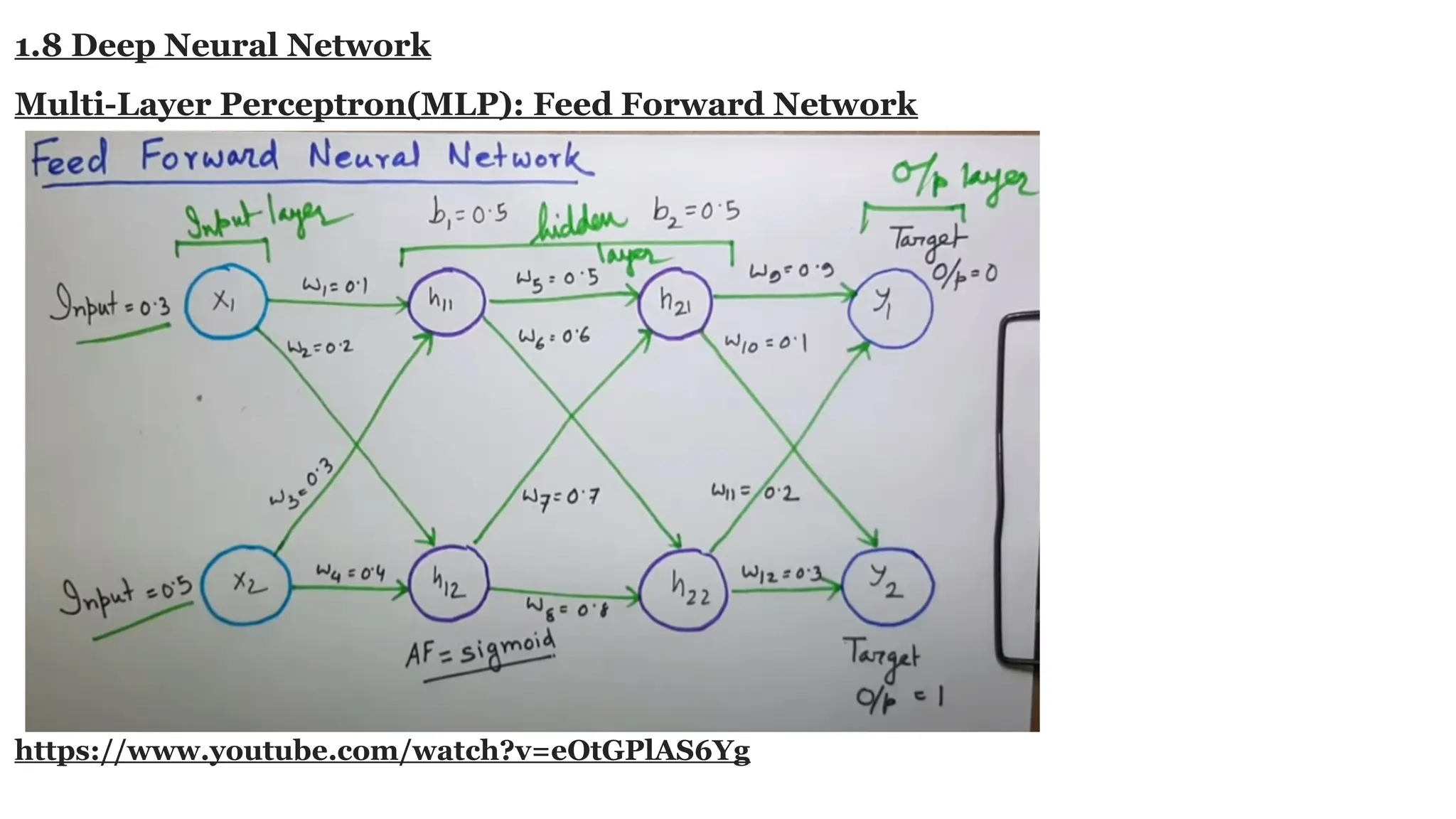
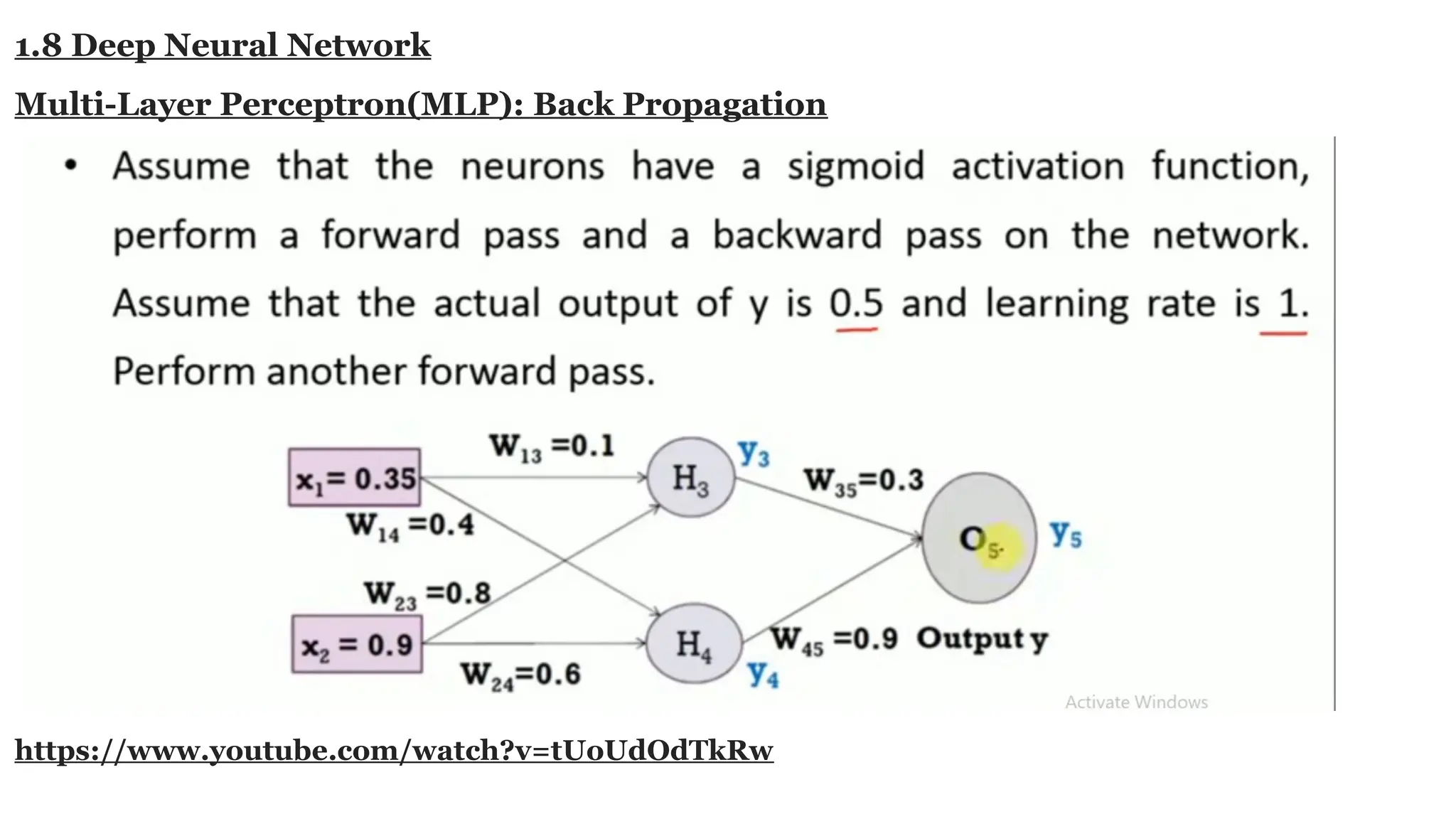
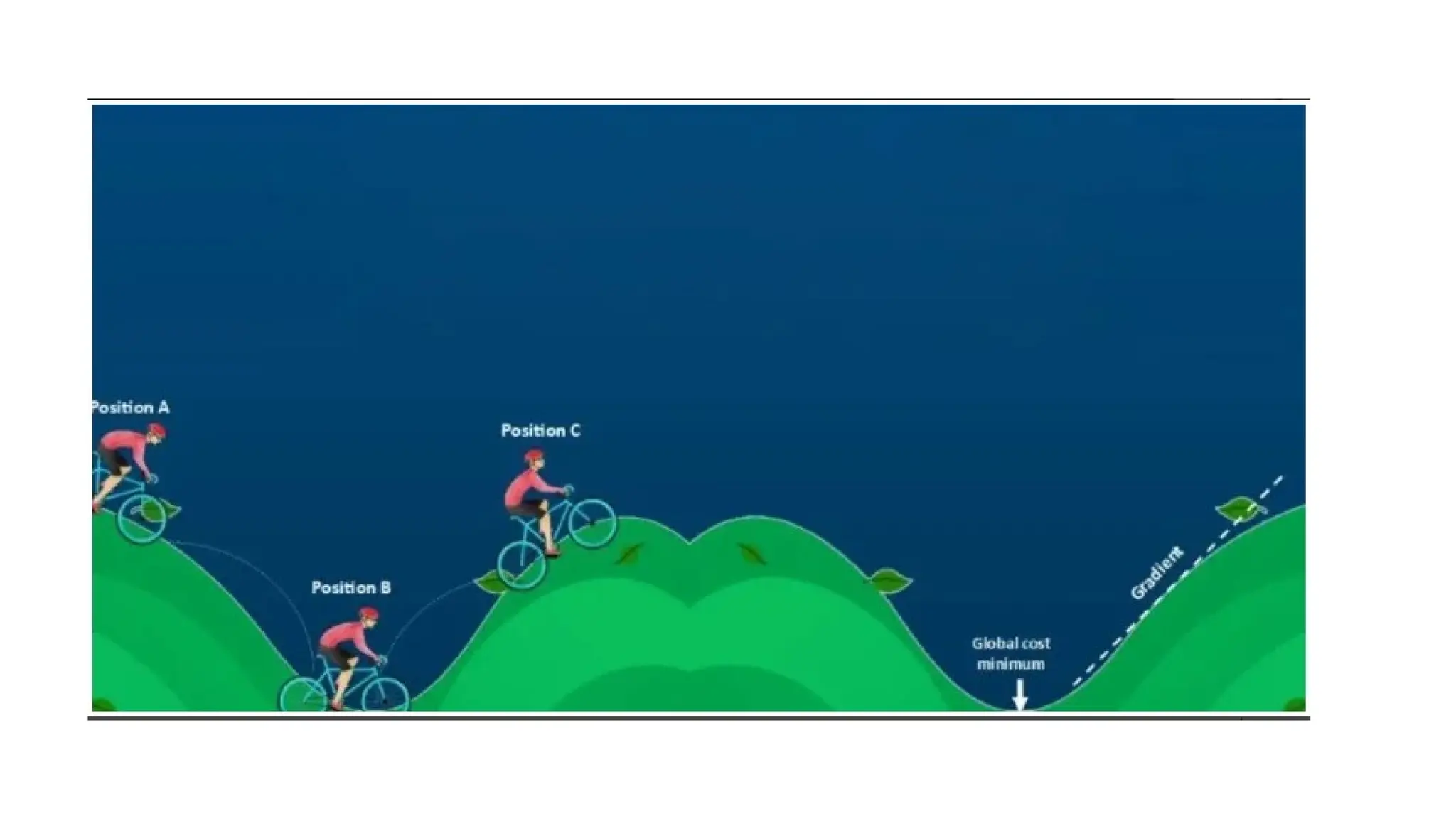
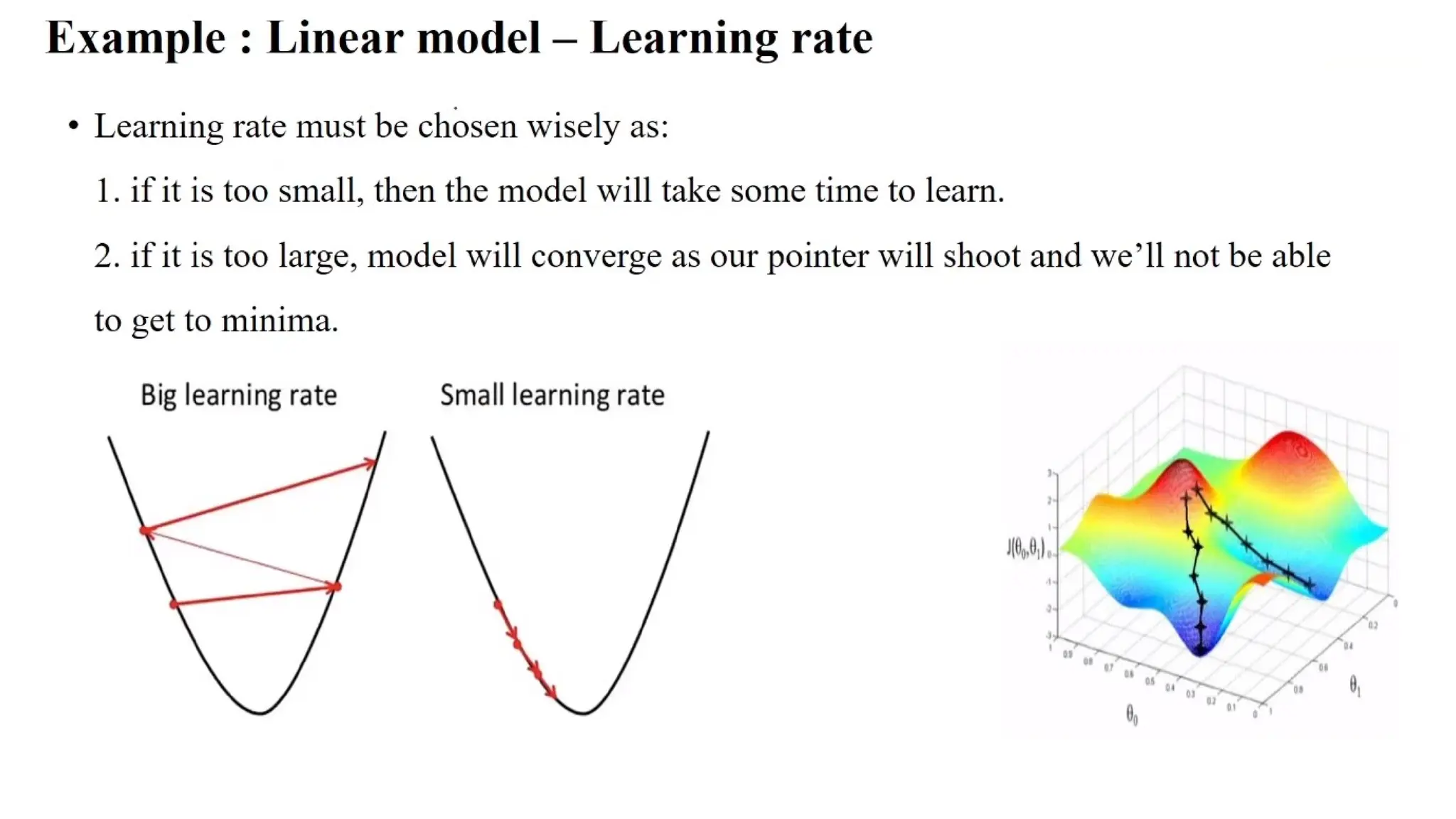
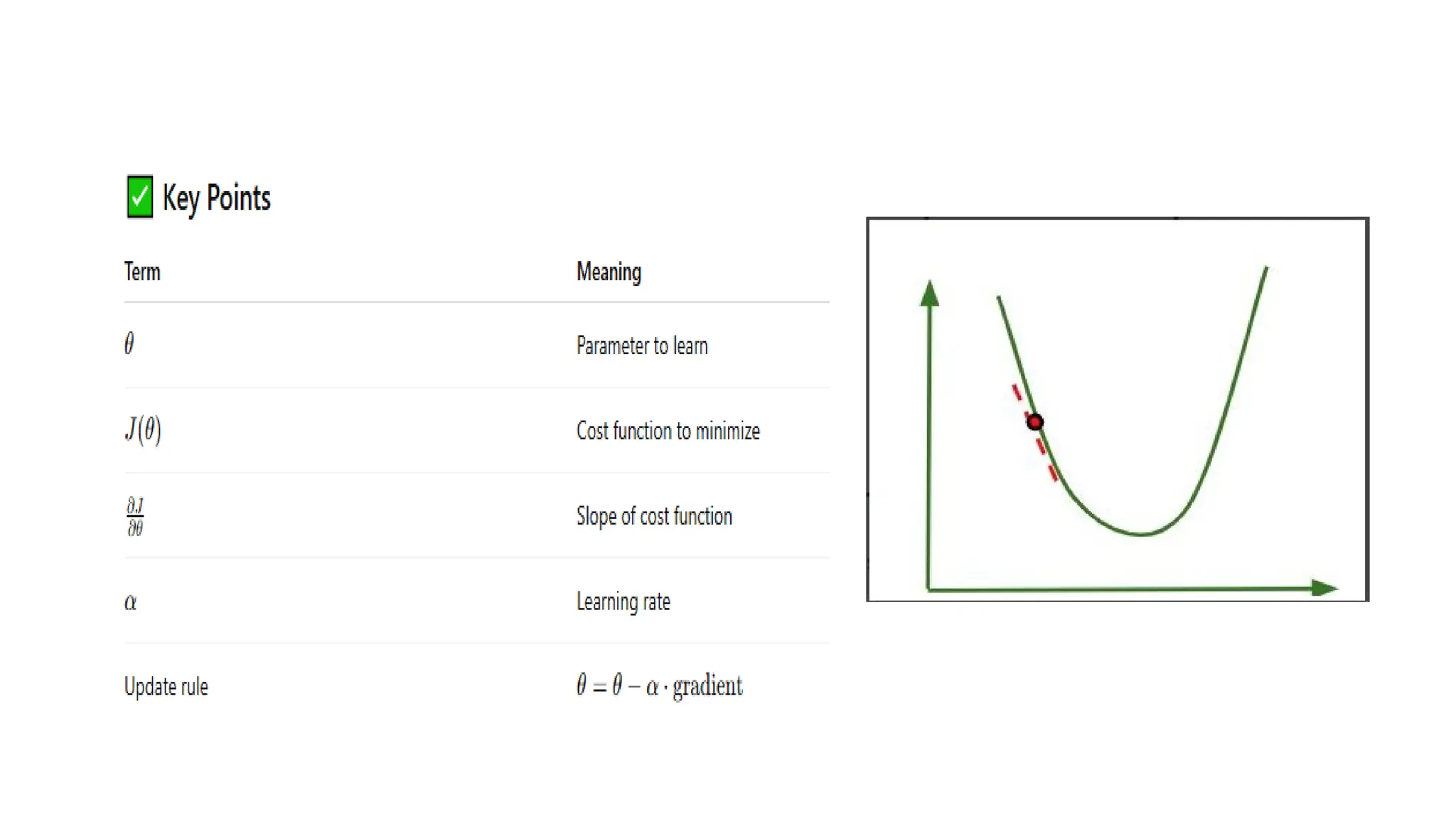
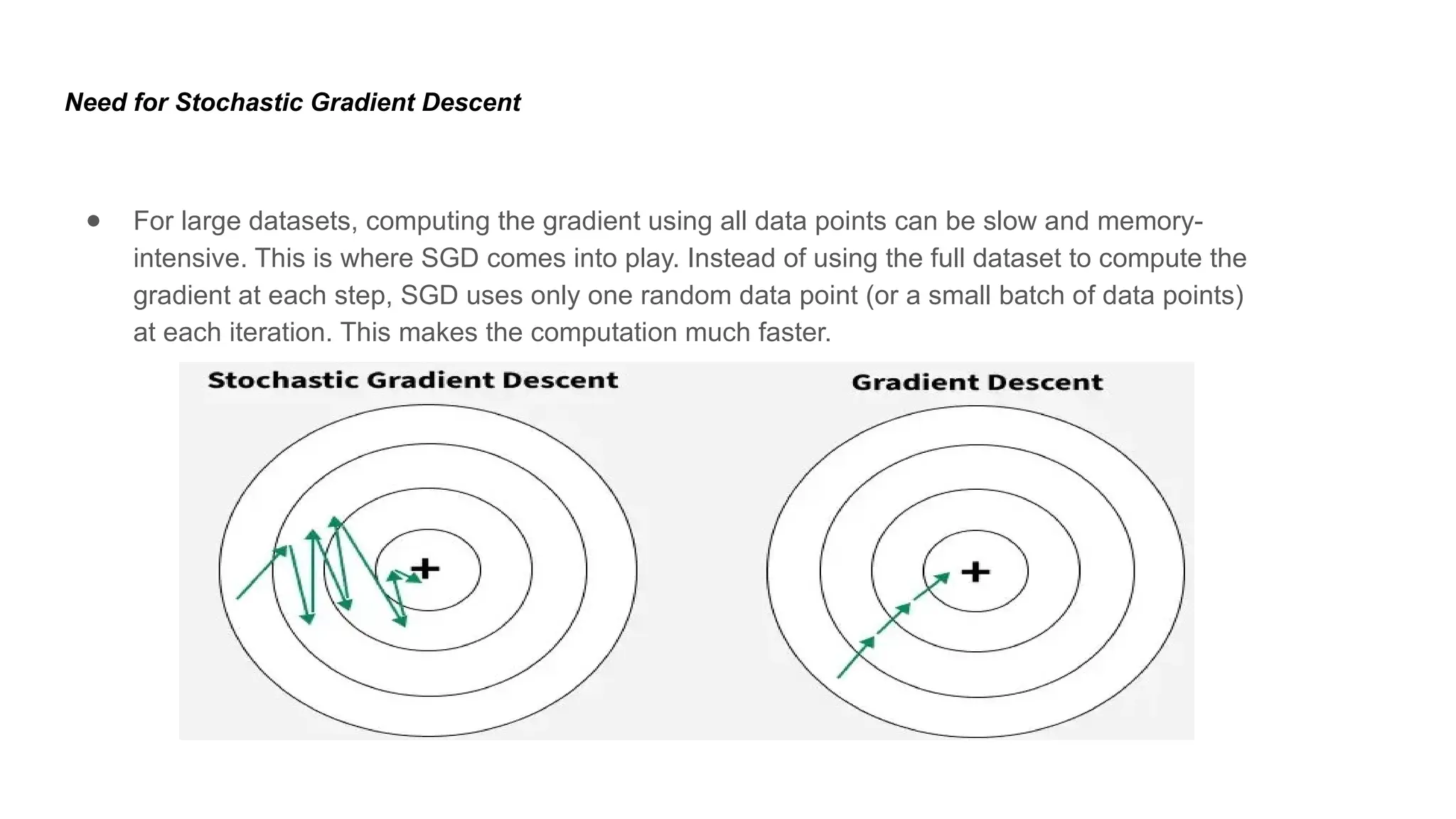
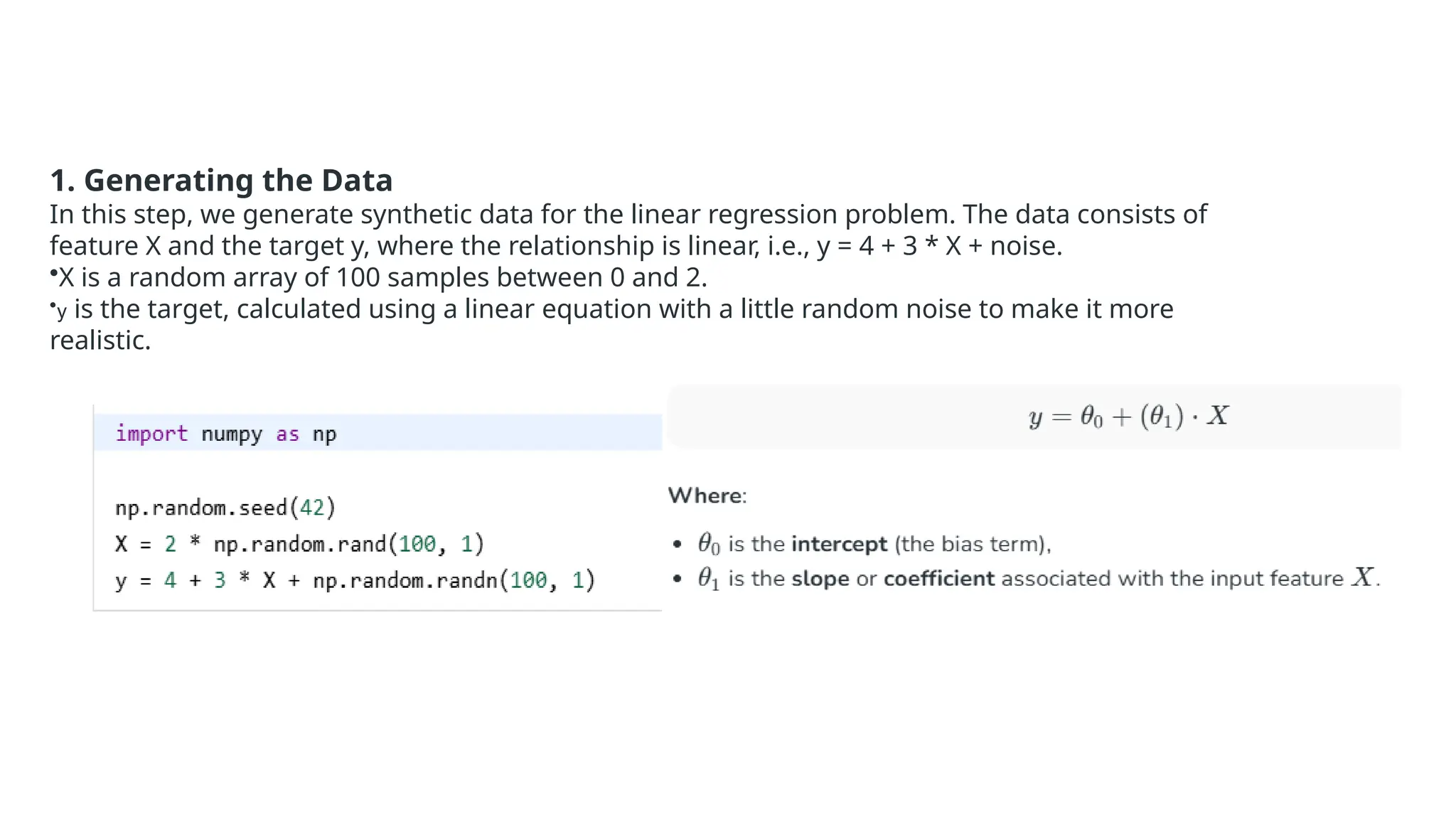
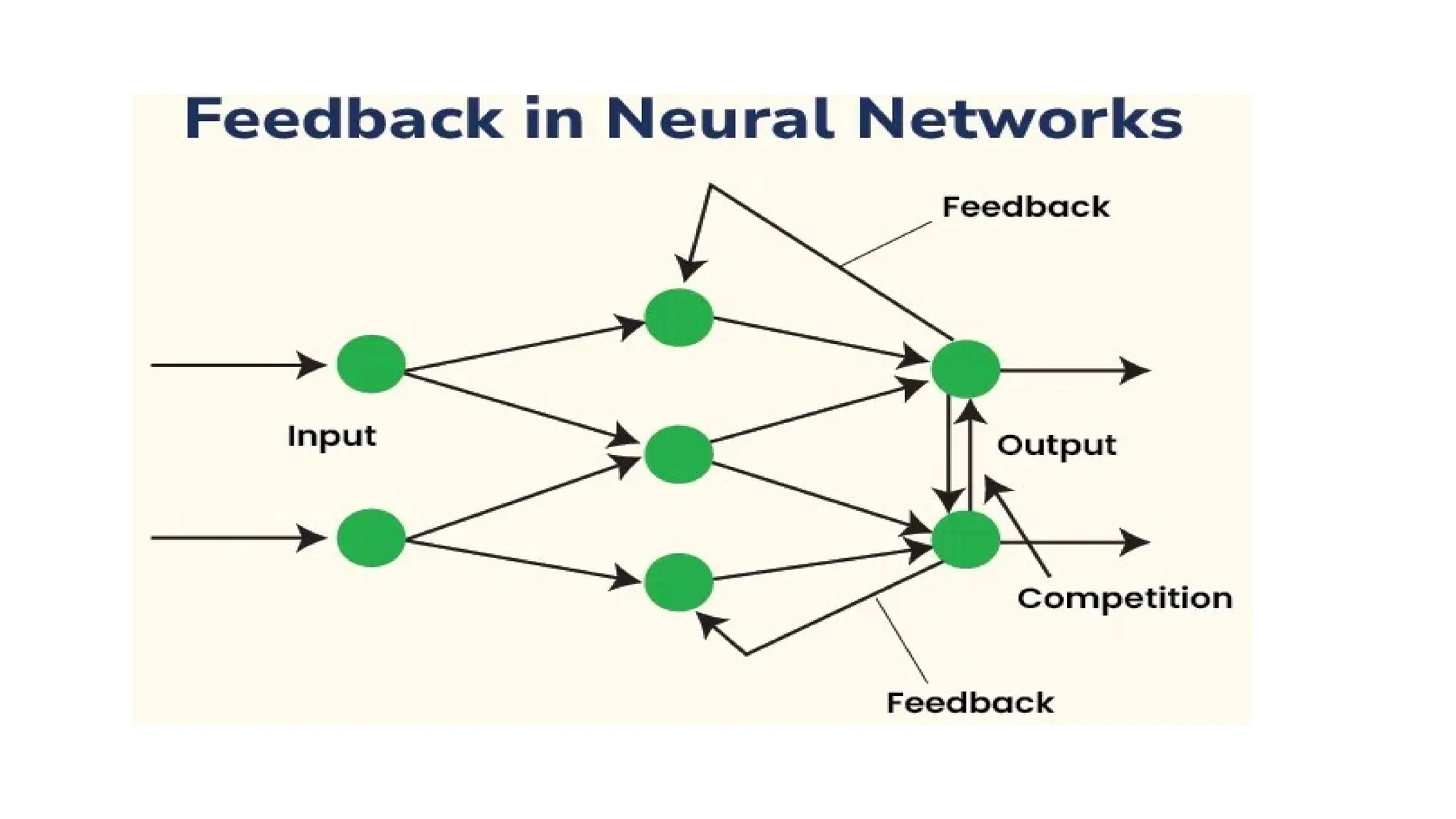
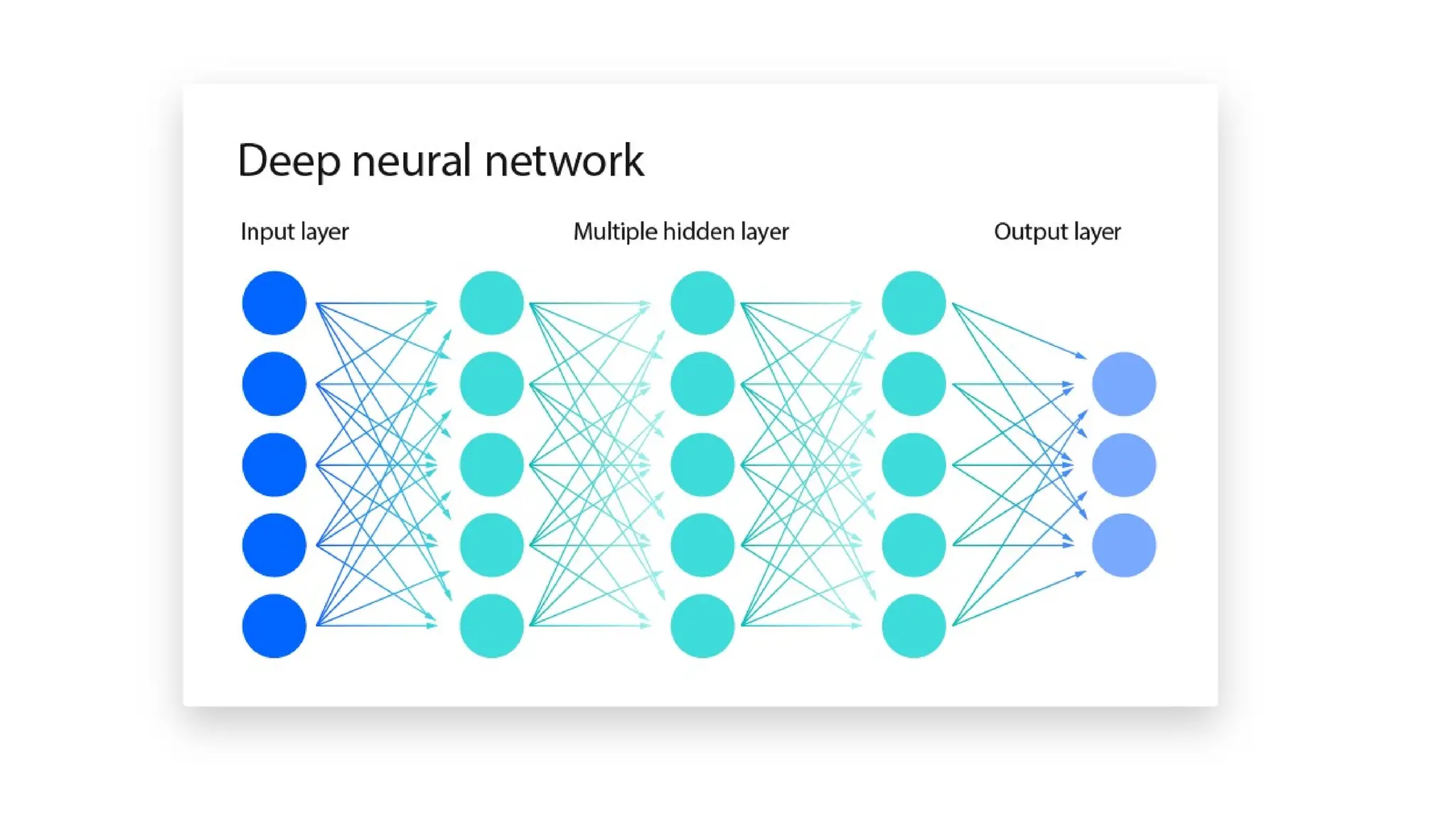
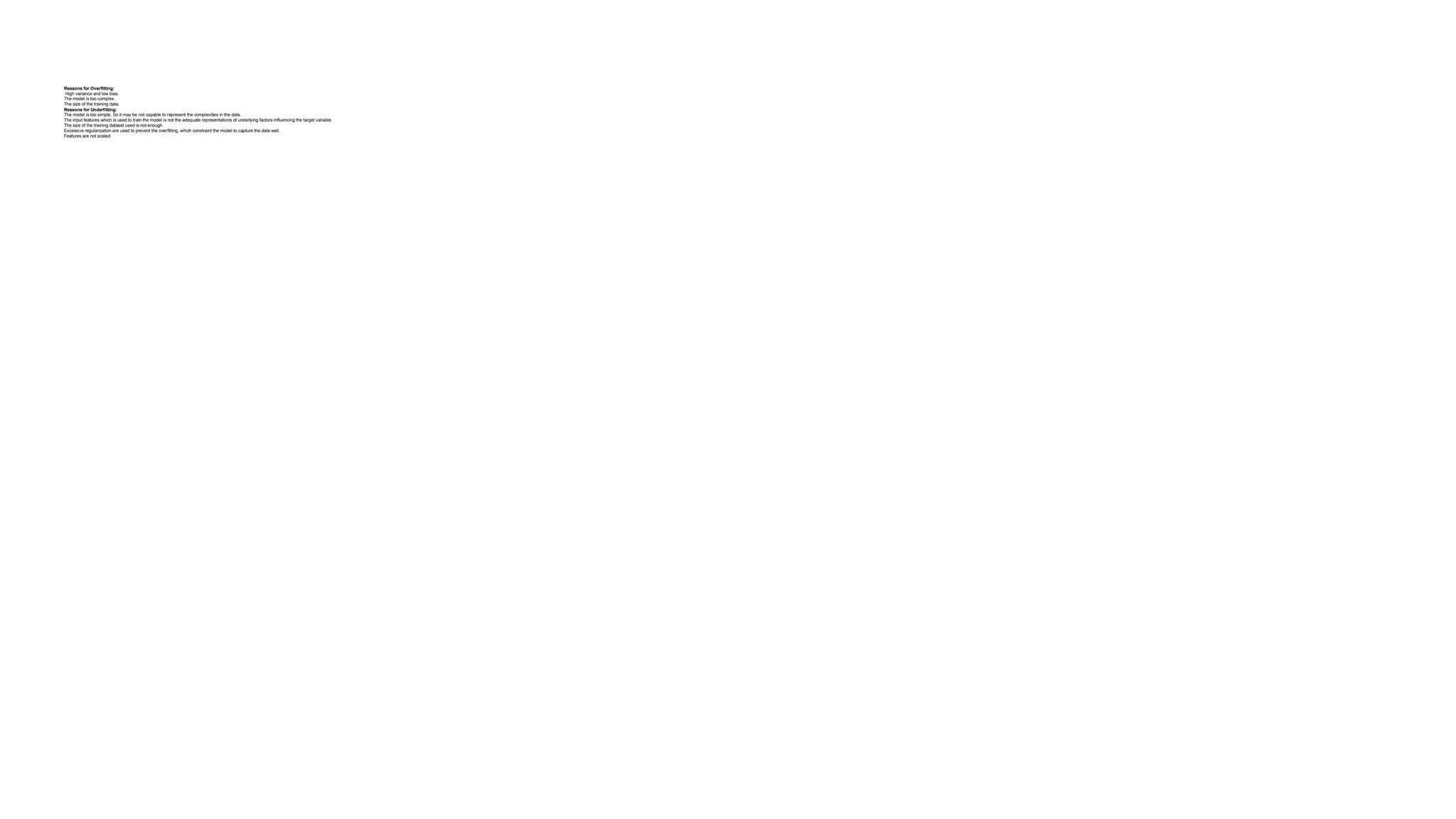Deep learning is a subfield of machine learning that uses artificial neural networks with multiple hidden layers to learn from vast amounts of data. By recognizing patterns in data through these layered networks, deep learning enables systems to learn, adapt, and make predictions on complex tasks like image recognition, natural language processing, and speech recognition without relying on human-engineered features.