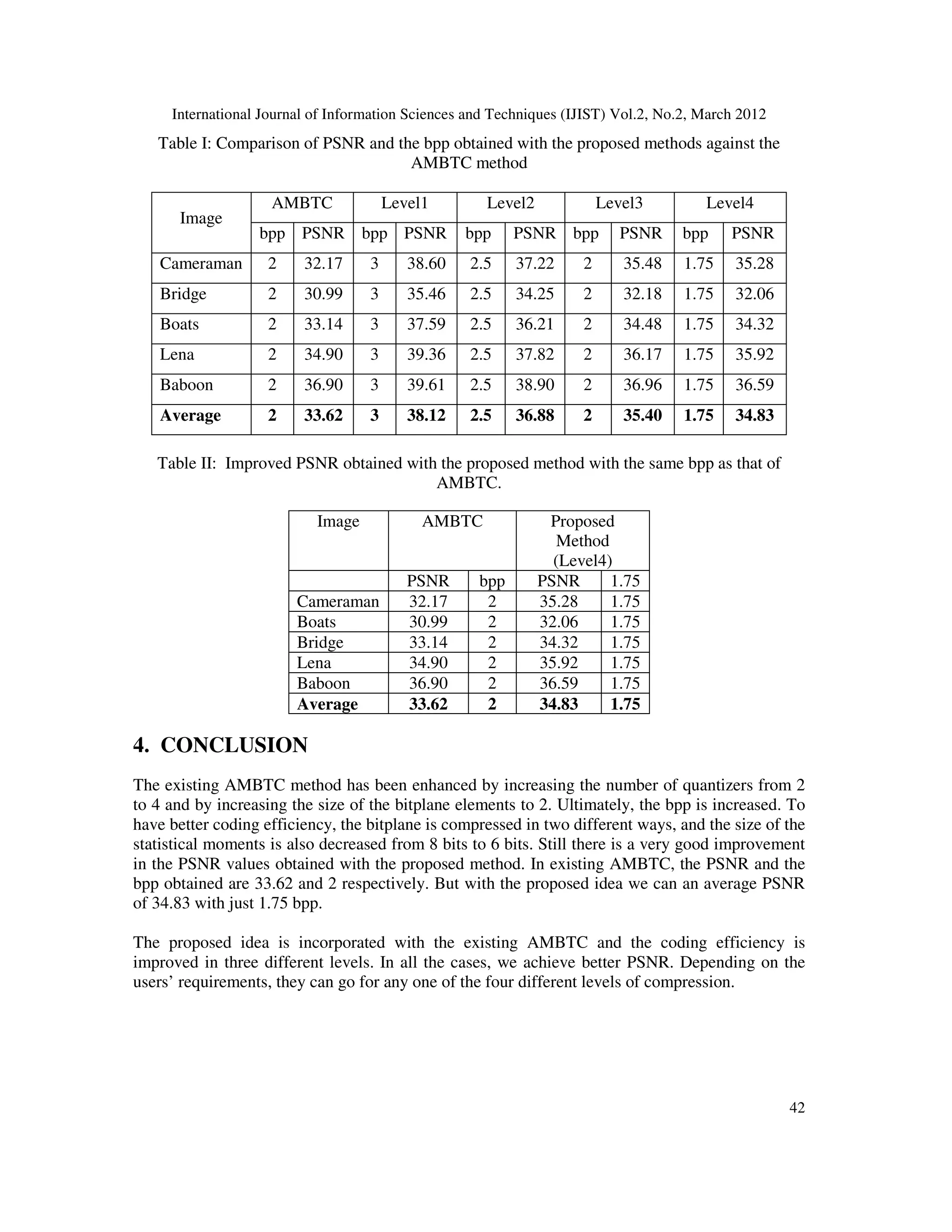
This document presents an enhanced version of Absolute Moment Block Truncation Coding (AMBTC) for image compression, improving the quality of reconstructed images significantly by increasing the number of quantizers from 2 to 4 and preserving more statistical moments. The proposed method demonstrates better Peak Signal-to-Noise Ratio (PSNR) and bits per pixel (bpp) compared to existing AMBTC techniques, with a final performance of 1.75 bpp and a PSNR of 34.83 after multiple compression levels. Experiments conducted on standard images show consistent improvements across various test cases.
![International Journal of Information Sciences and Techniques (IJIST) Vol.2, No.2, March 2012 DOI : 10.5121/ijist.2012.2204 35 Multi-Level Coding Efficiency with Improved Quality for Image Compression based on AMBTC Dr.K.Somasundaram1 and Ms.S.Vimala2 1 Department of Computer Science and Applications Gandhigram Rural Institute Gandhigram – 624 302 somasundaramk@yahoo.co.in 2 Department of Computer Science Mother Teresa Women’s University Kodaikanal – 624 102 vimalaharini@gmail.com ABSTRACT In this paper, we have proposed an extended version of Absolute Moment Block Truncation Coding (AMBTC) to compress images. Generally the elements of a bitplane used in the variants of Block Truncation Coding (BTC) are of size 1 bit. But it has been extended to two bits in the proposed method. Number of statistical moments preserved to reconstruct the compressed has also been raised from 2 to 4. Hence, the quality of the reconstructed images has been improved significantly from 33.62 to 38.12 with the increase in bpp by 1. The increased bpp (3) is further reduced to 1.75in multiple levels: in one level, by dropping 4 elements of the bitplane in such a away that the pixel values of the dropped elements can easily be interpolated with out much of loss in the quality, in level two, eight elements are dropped and reconstructed later and in level three, the size of the statistical moments is reduced. The experiments were carried over standard images of varying intensities. In all the cases, the proposed method outperforms the existing AMBTC technique in terms of both PSNR and bpp. KEYWORDS image, compression, bitplane, bpp, BTC, AMBTC 1. INTRODUCTION Predictive Coding and Transform Coding are few image coding techniques that are widely used in the real time implementation of image and video coding [1]. Block Truncation Coding (BTC) is an efficient image coding method [2]. It finds its use in real-time image transmission due to its simplicity, performance and superior channel resisting capability [3]. Various steps are being taken by the researchers now-a-days in enhancing the BTC based techniques to improve them in terms of both PSNR and coding efficiency. In [4], Kumar and Singh presented a BTC called EBTC for higher PSNR that that of BTC and AMBTC. Wu presented a probability based BTC to reduce the bitplane overhead [5]. Wang and Chong proposed an adaptive multi-level BTC [6]. Somasundaram and Vimala developed an efficient block truncation coding by exploiting the feature of inter-pixel correlation [7]. Choi and Ko devised a novel DPCM-BTC [8]. Natarajan and Rao proposed two modified BTC algorithms by using the ratio of moments [9]. In BTC, input](https://image.slidesharecdn.com/2212ijist04-210507041424/75/Multi-Level-Coding-Efficiency-with-Improved-Quality-for-Image-Compression-based-on-AMBTC-1-2048.jpg)
![International Journal of Information Sciences and Techniques (IJIST) Vol.2, No.2, March 2012 36 image is divided into small blocks of size 4 x 4 pixels. For each block, the mean of the pixel values is computed using the equation (1). ∑ = = m i i x m x 1 1 (1) where m is the total number of pixels in a block. The standard deviation σ is computed using the equation (2). ( ) m x x i 2 − = σ (2) Using the mean, the bitplane (B) of 0s and 1s is generated using the equation (3). 0 1 else then x x if i ≥ (3) Two quantizers q1 and q2 are computed for each block using the equations (4) and (5). x x for p m p x q i ≥ − + = 1 σ (4) x x for p p m x q i < − − = 2 σ (5) The compressed image is stored or transmitted as a set of {B, q1, q2}. While reconstructing the image, the 1s in the bitplane are replaced with q1 and 0s are replaced with q2. The quality of the reconstructed image is computed with the Peak Signal to Noise Ratio (PSNR) using the equation (7). To compute the PSNR, the Mean Square Error (MSE) is computed using the equation (6). ( ) ( ) ∑ − = 2 2 , ) , ( 1 j i I j i I MxN MSE i (6) where MxN is the number of rows and columns of pixels in an image. I1 is the input image and I2 is the reconstructed image. = MSE xLog PSNR 2 10 255 10 (7) Various BTC approaches have been proposed in the past [10]. Absolute Moment Block Truncation Coding (AMBTC) is an improved version of BTC, in which, instead of computing standard deviation (σ ) that involves more multiplications, two quantizing levels high mean (hMean) and low mean (lMean) are computed using the equations (8) and (9). . 1 1 x x if x p hMean i p i i ≥ = ∑ = (8) where p is the number of pixels in a block whose values are greater than or equal to mean. . 1 1 x x if x q lMean i p i i ≤ = ∑ = (9)](https://image.slidesharecdn.com/2212ijist04-210507041424/75/Multi-Level-Coding-Efficiency-with-Improved-Quality-for-Image-Compression-based-on-AMBTC-2-2048.jpg)
![International Journal of Information Sciences and Techniques (IJIST) Vol.2, No.2, March 2012 37 where q is the number of pixels in a block whose values are less than mean. The PSNR obtained with the AMBTC is better than that of BTC. The improved variants of AMBTC: The Minimum Mean Square Error (MMSE). It is an iterative procedure to refine the quantizers that are generated [11] in consecutive iterations, the Minimum MAE Quantization (MMAE) [6] [12]. In another variant of BTC, called the New Look-up Table BTC Technique, the feature of inter pixel redundancy is used to reduce the bit rate further [13]. In EBTC [14], the blocks are categorized into high detail blocks and low detail blocks. For low detail blocks, only the mean alone is preserved thus leading to reduced bit rate. Like wise, much of study is conducted now-a-days to improve the BTC based techniques both in terms of bpp and the PSNR values. In this paper, we have enhanced the existing AMBTC. In AMBTC, only two quantizers are used and hence the pixels in a reconstructed block take only either one of the two qantizers. In the proposed method (Improved AMBTC - IAMBTC), we have increased the number of quantizers to 4 and hence the number of bits used to represent the quantizing levels is raised. The remaining part of the paper is organized as follows: The proposed method is explained in Section 2, the results are discussed in section 3 and the conclusion is given in Section 4. 2. PROPOSED METHOD In this method, the input image is divided into blocks of size 4 x 4 pixels. For each block, the high mean and the low mean, called the quantizers are computed using the equations (8) and (9) as in AMBTC. While encoding, to generate four quantizers, the step value is computed using the equation (10). sv = (hMean-lMean)/3 (10) The four quantizers, other than the hMean and lMean are computed using the equations (11) thru. (14). Q1 = lMean (11) Q2 = lMean + sv (12) Q3 = Q2 + sv (13) Q4 = hMean (14) For each block, the bitplane is generated as follows: if the pixel value is closer to Q1, it is coded as 00. If the pixel value is closer to Q2, it is coded as 01, if closer to Q3, it is coded as 10 and if closer to Q4, it is coded as 11. Now a bitplane of size 32 bits is generated rather than 16 bits. As the quantizers Q2 and Q3 can be computed at the destination (decoding stage), only the two quantizers Q1 and Q4 are preserved along with the bitplane. The quantizers Q2 and Q3 are computed only when encding and decoding take place and not preserved along with the bitplane. The extended bitplane/quantizers are encoded in four different levels. In the first level, for each input image block, a bitplane of size 32 bits along with the quantizers Q1 and Q4 of size 16 bits are stored leading to a bit rate of 3 bpp. As a step towards improving the coding efficiency, the feature of inter-pixel redundancy is exploited. Due to spatial redundancy, it is assumed that the nearest pixels will have more or less](https://image.slidesharecdn.com/2212ijist04-210507041424/75/Multi-Level-Coding-Efficiency-with-Improved-Quality-for-Image-Compression-based-on-AMBTC-3-2048.jpg)




![International Journal of Information Sciences and Techniques (IJIST) Vol.2, No.2, March 2012 43 REFERENCES [1] Jain A.K., “Image Data Compression: A Review”, Proc. IEEE, 1981, 69, pp. 349-380. [2] Delp E.J. and Mitchell O.R., “Image Compression using Block Truncation Coding”, IEEE Transactions on Communication, Vol. COM-27, pp. 1335-1342, Sept. 1979. [3] Bing Zeng and Yrjo Neuvo, “Interpolative BTC Image Coding with Vector Quantization”, IEEE Transactions on Communications, Vol. 41, No. 10, October 1993. [4] Kumar A. and Singh P., “Enhanced Block Truncation Coding for Gray Scale Image”, International Journal of Comput. Tech. Appl., 2: 525-530, 2011. [5] Wu Y.G., “Block Truncation Image Bitplane Coding”, Optical Engineering, 41: 2476-2478, 2002. [6] Wang J. ad Chong J.W., “Adaptive Multi-level Block Truncation Coding for Frame Memory Reduction in LCD Overdrive”, IEEE Transactions on Consum. Elect. 56: 1130-1136, 2010. [7] Somasundaram K. and S.Vimala, “Efficient Block Truncation Coding for Image Compression”, International Journal of Computer Science and Engineering, 2: 2163-2166, 2010. [8] Choi K.S. and KO S.J., “Improved differential Pulse Code Modulation – Block Truncation Coding Method adopting two-level Mean Squared Error Near Optimal Quantizers”, Optical Engineering, 50: 47001-47007. [9] Natarajan S. and Rao Y.V.R., “Ratio Modified Block Truncation Coding Algorithm for Reduced Bitrates”, Imaging Science Journal, 50: 25-31. [10] P.Franti, O.Navelainen and T.Kaukoranta, “Compression of Digital Images by Block Truncation Coding: A Survey”, The Computer Journal, Vol. 37, No. 4, pp. 308- 332, 1994. [11] Madhu Shandilya and Rajesh Shandilya, ”Implementation of Absolute moment Block Truncation Coding Scheme Based on Mean Square Error Criterion”, SDR 03 Technical Conference and Product Exposition. [12] Lucas Hui, “An Adaptive Block Truncation Coding Algorithm for Image Compression”, IEEE, PP.2233-2235, 1990. [13] Pasi Franti, Olli Nevalainen and Timo Kaukoranta, ”Compression of Digital Images by Block Truncation Coding:A Survey”, The Computer Journal, Vol.37, No.4, 1994. [14] K.Somasundaram and S.Vimala, “Efficient Block Truncation Coding”, International Journal on Computer Science and Engineering Vol. 02, No. 06, 2163-2166, 2010. Authors Dr.K.Somasundaram was born in the year 1953. He received the M.Sc. Degree in Physics from University of Madras , Chennai, India in 1976, the Post Graduate Diploma in Computer Methods from Madurai Kamaraj University, Madurai, India in 1989 and the Ph.D. Degree in Theoretical Physics from Indian Institute of Science, Bangalore, India in 1984. He is presently the Professor and Head of the Department of Computer Science and Applications, Gnadhigram Rural Institute, Gandhigram, India. From 1976 to 1989, he was a Professor with the Department of Physics at the same Institute. He was previously a Researcher at the International Center for Theoretical Physics, Trieste, Italy and a Development Fellow of Common Wealth Universities at the School of Multimedia, Edith Cowan University, PERT, Australia. His research Interests are in Image Processing, Image Compression and Medical Imaging. He has published more than 100 papers in National and International Journals like IEEE Transactions on Multimedia, Computers in Biology and Medicine (Elsevier), AEU, International Journal on Electronics and Communications, IEEE Transactions on Plasma Science, etc. He has attended several International conferences in USA, Australia, Italy, Singapore and Hungary. He has published three books: Programming in JAVA2 and Advanced Programming in JAVA2, (both by Jaico Publishing, Mumbai) are his best selling books. He is a Life Member of India Society for](https://image.slidesharecdn.com/2212ijist04-210507041424/75/Multi-Level-Coding-Efficiency-with-Improved-Quality-for-Image-Compression-based-on-AMBTC-9-2048.jpg)
