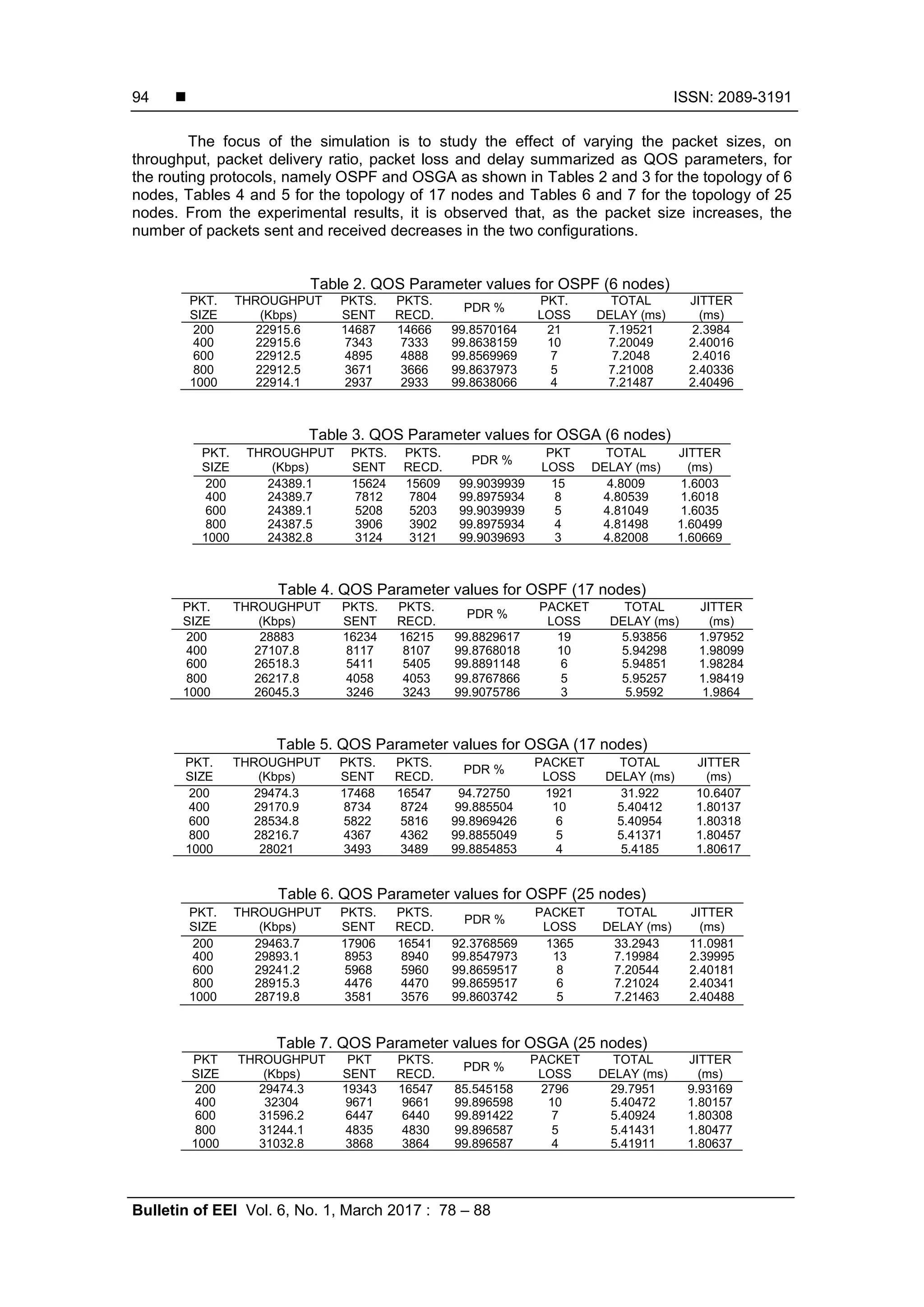
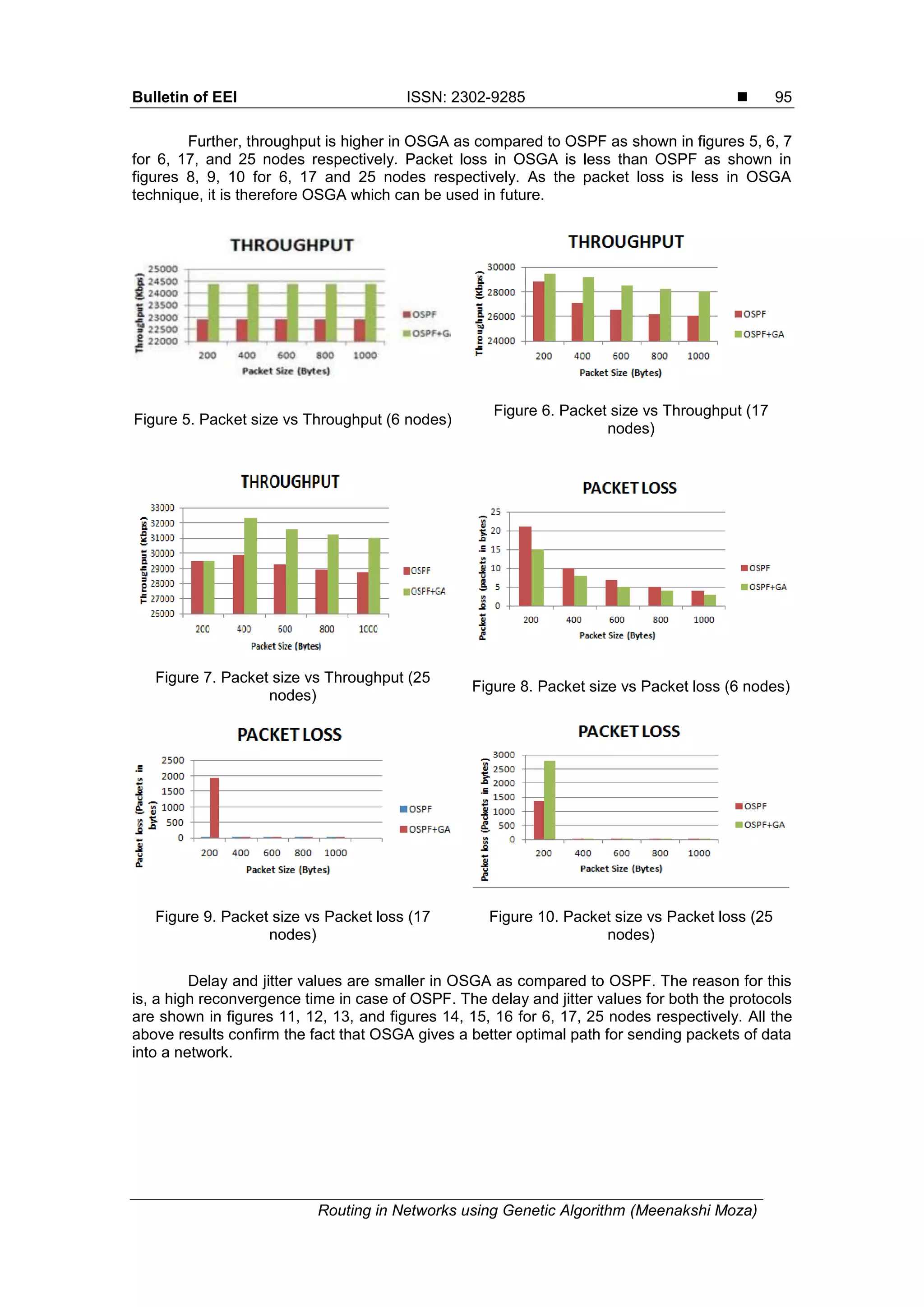
This document discusses a method for optimizing routing in computer networks by integrating a genetic algorithm with the Open Shortest Path First (OSPF) protocol, resulting in the Open Shortest Genetic Algorithm (OSGA). It highlights the importance of efficient path selection for communication, considering various performance metrics and QoS parameters. The paper includes a literature review, network analysis methodology, and performance evaluation using simulations to demonstrate the advantages of OSGA over traditional OSPF.
![Bulletin of Electrical Engineering and Informatics ISSN: 2302-9285 Vol. 6, No. 1, March 2017, pp. 88~98, DOI: 10.11591/eei.v6i1.574 88 Received November 6, 2016; Revised January 6, 2017; Accepted January 20, 2017 Routing in Networks using Genetic Algorithm Meenakshi Moza*, Suresh Kumar CSE Department, F.E.T., Manav Rachna International University, India *Corresponding author, email: meenakshi.fet@mriu.edu.in Abstract With the increase in traffic, internet service providers are trying their best to provide maximum utilization of resources available. The current traffic load has to be taken into account for computation of paths in routing protocols. Network applications; require the shortest paths to be used for communication purposes. Addressing the selection of path, from a known source to destination is the basic aim of this paper. This paper proposes a method of calculating the shortest path for a network using a combination of Open shortest path first and Genetic Algorithm (OSGA). Genetic Algorithm is used in this paper for optimization of routing. It helps in enhancing the performance of the routers. Keywords: genetic algorithm, open shortest path first, quality of service, chromosome, mutation, routing 1. Introduction Computer Network is a collection of autonomous computers interconnected for the purpose of communication and resource sharing [1]. The interconnection can be done using the public telephone network, dedicated leased lines or any other medium. The transmission media used for interconnection may be wired or wireless. The demands of users of computer networks are changing very fast. They want information anytime, anywhere. The networks are not only used for merely transferring data, but also for other applications like audio and video conversation, video streaming, etc. These applications have special requirements in terms of reliability, bandwidth, jitter, delay etc. The network should possess these qualities for satisfying the demands of the users. Routing is a selection of the best path for packets to traverse in a network [2-4]. Selection of the path means to apply a routing metric like hop count, delay, bandwidth, for the evaluation of a path, which is best for a packet to travel. Routing algorithms facilitate in the determination of the path [5]. They help in initialization and maintenance of routing tables, which contain routing information. When a packet is received by a router, the destination address is checked and it is the duty of routing algorithm for association of this destination address with the next hop. Routing tables are built, using a lot of routing algorithms which help to find the path from source to destination. Open Shortest Path First (OSPF) is one such link state routing algorithm, which helps us to find the shortest path between each source & destination [6-9]. OSPF can run on most routers and makes use of shortest path first (SPF) algorithm developed by Dijkstra. The basic steps carried out in OSPF are as follows: a. Step 1: The routers are synchronized by exchanging the hello packets. b. Step 2: The topology of the network is shared by exchanging link state packets. c. Step 3: Each router then creates a shortest path tree from the topology information received in the step 2. The limitation in case of OSPF is overloading, in the shortest path. The arrival of the packets at the desired destination with the delay or queuing on the way or router processing can result in service quality being affected. All these limitations can be taken care of, by optimization of the IP network [10-12]. It can therefore be safely said that the basis of planning and managing networks is routing optimization which is achieved by applying GA to the network. In this paper, it is proposed to extend OSPF by applying GA on OSPF resulting in the Open shortest genetic algorithm (OSGA). Here, a potential solution to the problem are encoded in a](https://image.slidesharecdn.com/115feb177nov16574-899-1-smeditari-210608024538/75/Routing-in-Networks-using-Genetic-Algorithm-1-2048.jpg)
![Bulletin of EEI ISSN: 2302-9285 Routing in Networks using Genetic Algorithm (Meenakshi Moza) 89 way that the computer can process. The easiest way is to encode solutions as binary sequences of 0’s and 1’s which has been adopted in this paper [13-16]. This paper is organized into five sections. Section 1 provides the introduction to routing. Section 2 discusses the literature review. Section 3 talks about network analysis using GA. Section 4 deals with the performance evaluation in terms of methodology adopted and how NS3 is used for analyzing the behavior of the network under consideration. Also it talks about the variations of certain parameters for the routing protocols under consideration. In other words, this section comprises the complete result analysis. Section 5 discusses the conclusions drawn and the future scope. 2. Literature Review M. Goyal et al. (2006) state that a tradeoff is required between load processing, traffic control and speed, after re convergence, due to the change in topology. Because of the nature and size of networks being served by OSPF has changed, therefore there is a requirement for reevaluation of OSPF. In order to modify OSPF, we cannot increase load on routers because overloading of Central Processing Unit (CPU) results in routing instability of networks. In this paper, an environment which is broadcast and Local Area Network (LAN) in nature is taken and it is seen that many Designated Router (DR) elections are required by a router before settling on the DR, Backup Designated router (BDR) identification. The reason for this is given as, that routers before being able to establish communication which is bidirectional in nature, are out of the wait state. Also more than one router can initially elect itself as BDR, so many DR elections take place and then the routers later give it up. In addition to this, a forty second wait time results in settling process of the DR / BDR to get delayed. Certain modifications are put forward in this paper to remove the above limitations. The first change is to restart wait timer as soon as a hello message (one way) is obtained. The next change is for wait timer to have a value so that the router can have bidirectional communication with that neighbor, who had sent a hello message which had restarted the wait timer. Also for a router which is not in a wait state, it should be possible to avoid DR elections, if it establishes bidirectional communication, when some of its neighbors are not bidirectional. This is possible by introducing a new wait 2 state. The last modification required is that on being elected a DR / BDR, a router should send a hello message immediately so that everybody knows about it. M. Goyal et al. (2011) states the steps required to improve the scalability and convergence in OSPF. They further discuss that, recovering from a network failure in original OSPF, would take tens of seconds, but in real time, applications like Voice Over Internet Protocol, used now, the breakdown of a network for such a length of time is not possible. The paper has carried out an extensive survey and found out that, in case of topology change, fast convergence is the talk of the day and the below mentioned steps need to be carried out to fulfill the same. The first step is detection of failure at a faster rate. The next step is establishing adjacencies, lesser in number, but faster in speed. The third step is optimization in generating link state advertisements and the last step is optimization in calculating routing tables. The paper also stated that, the changes that are to be incorporated in the operation of OSPF, should not result in compromising the correctness of the protocol in any improbable scenario also. M. Shand et al. (2013) in this paper, describe a technique which can be used in combination with link state protocols for prevention of transient loops. The technique consists of, formation of correct sequence, of the updates of forwarding information base (FIB) on routers. They further state in the paper that whenever a router shutdown occurs, any router R1 should not update its forwarding information base till all the other routers which are sending traffic through R1 and the router that has been shut down, have updation of their FIB’s. Also, they describe, that when a router is put to service, any router R2 has to update its FIB, before all those routers which will use R2 to reach the affected router. They further analyzed and listed the steps required to apply updation of the FIB. The first step is deduction of change in topology followed by the decision as to whether updates of ordered FIB apply. The next step is to compute the order that is computation of rank by a router which helps in the determination of the time at which FIB update can be performed. The last step is to accelerate the ordered convergence. This is comprised of usage of completion messages to increase the speed of convergence. This is done by means of a router which informs all the routers about completion of changes of FIB. So the routers can go for updation of their FIB with less of delay. A wait list of](https://image.slidesharecdn.com/115feb177nov16574-899-1-smeditari-210608024538/75/Routing-in-Networks-using-Genetic-Algorithm-2-2048.jpg)




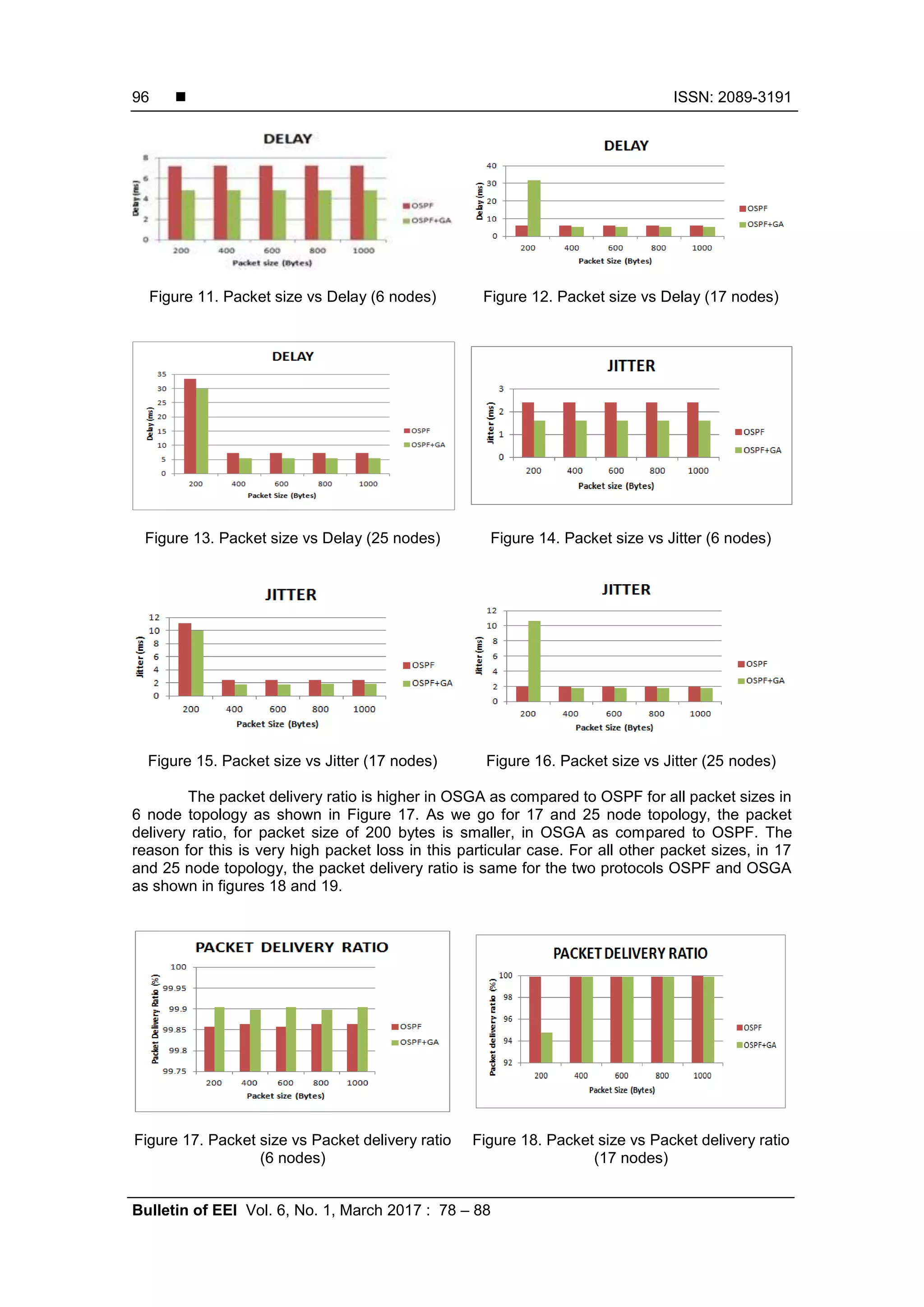
![Bulletin of EEI ISSN: 2302-9285 Routing in Networks using Genetic Algorithm (Meenakshi Moza) 97 Figure 19. Packet size vs Packet delivery ratio (25 nodes) After studying all the parameters it can be said that OSGA seems to be a better technique, for finding the most optimal path for sending packets of data into a network. 5. Conclusion and Future Scope This paper proposes the usage of GA in combination with OSPF (OSGA) for finding a optimal path between source and destination. Length of chromosomes (paths) is dependent on a number of existing nodes in the network [17-19]. The simulation is carried out in NS3 environment. This method can be used in the future for high speed networks. The results tell us that by setting the GA parameters properly (Size of population, Number of generations), the algorithm gives a better result than OSPF. References [1] Lee YO. Improving Efficiency and Effectiveness of Multipath Routing in Computer Networks (Doctoral dissertation, Texas A&M University). 2012. [2] Chandel GS, Gupta R, Kushwaha A. Implementation of Shortest Path in Packet Switching Network Using Genetic Algo. International Journal of Advanced Research in Computer Science and Software Engineering. [3] Leung R, Liu J, Poon E, Chan AL, Li B. MP-DSR: A QoS-aware multi-path Dynamic Source Routing Protocol for the Wireless Ad-hoc Networks. In Local Computer Networks, 2001. Proceedings. LCN. 26th Annual IEEE Conference. 2001: 132-141. [4] Sharma S, Bhardwaj SK. Experimental Analysis of OLSR and DSDV Protocols on NS-2.35 in Mobile Ad-Hoc Networks. International Journal of Computer Network and Information Security. Jul 1 2015; 7(8): 21. [5] Al-Ghazal M, El-Sayed A, Kelash H. Routing Optimization using Genetic Algorithm in Ad hoc Networks. In 2007 IEEE International Symposium on Signal Processing and Information Technology Dec 15 2007: 497-503. [6] Ren W, Kang C, Li Y, Gong L. Chaotic Immune Genetic Hybrid Algorithms and Its Application. Indonesian Journal of Electrical Engineering and Computer Science. Feb 1 2013; 11(2): 975-84. [7] Goyal M, Soperi M, Baccelli E, Choudhury G, Shaikh A, Hosseini H, Trivedi K. Improving Convergence Speed and Scalability in OSPF: A survey. IEEE Communications Surveys & Tutorials. Apr 2 2012; 14(2): 443-63. [8] Goyal M, Xie W, Hosseini SH, Vairavan K, Rohm D. Improving OSPF dynamics on a broadcast LAN. Simulation. Feb 1 2006; 82(2): 107-29. [9] Shand M, Bryant S, Previdi S, Filsfils C, Francois P, Bonaventure O. Framework for Loop-free Convergence using the Ordered Forwarding Information Base (ofib) approach. 2013. [10] Obeidat A, Ebed M. Improving the Performance of Networks using Genetic Algorithm. Proc. of the International Conf. on Advances in Computer and Information Technology, ACIT, 2012. [11] Sooda K, Nair TR. A Comparative Analysis for Determining the Optimal Path using PSO and GA. arXiv preprint arXiv 1407.5327. Jul 20 2014. [12] Kavitha R, Anusuya V. Genetic algorithm for Finding Shortest Test Path in Networks. International Journal of Fuzzy Mathematical Archive. 2013; (2): 43–48. [13] Fadil YA. Routing using Genetic Algorithm for large Networks. Diyala Journal of Engineering Sciences. Dec 2010; 3(02). 53-70. [14] Krishna G, Pandey NK, Bajpai S. Optimal Path Routing in Variable Data Network using Genetic Algorithm. International Journal of Engineering Science and Humanities. 2012. [15] Kumar R, Kumar M. Exploring Genetic algorithm for Shortest Path Optimization in Data Networks. Global Journal of Computer Science and Technology. Oct 25 2010; 10(11).](https://image.slidesharecdn.com/115feb177nov16574-899-1-smeditari-210608024538/75/Routing-in-Networks-using-Genetic-Algorithm-10-2048.jpg)
![ ISSN: 2089-3191 Bulletin of EEI Vol. 6, No. 1, March 2017 : 78 – 88 98 [16] Hassan M, Younes A, Hassan MR, Abdo H. Solving the File Allocation Problem in the Distributed Networks by UsingGenetic Algorithms. International Journal of Information and Network Security. Jan 1 2013; 2(1):109. [17] Baboo SS, Narasimhan B. Genetic Algorithm Based Congestion Aware Routing Protocol (GA-CARP) for Mobile Ad Hoc Networks. Procedia Technology. Dec 31 2012; 4: 177-81. [18] Hamed AY. A Genetic Algorithm for finding the K Shortest Paths in a Network. Egyptian Informatics Journal. Dec 31 2010; 11(2): 75-9. [19] Moza M, Kumar S. Improving the Performance of Routing Protocol using Genetic Algorithm. International Journal of Computer Network & Information Security. Jul 1 2016; 8(7). BIOGRAPHIES OF AUTHORS Meenakshi Moza born in Srinagar on 25th Jan 1965, did her B.E from R.E.C. Srinagar (Kashmir) in Electronics and Communication. She completed her Mtech from Y.M.C.A Faridabad. She is pursuing her Phd in the field of computer networks. She has 14 years of experience in teaching and 8 years of experience in industry namely Onida, Avery India. Total number of research publications are 14. Dr. Suresh Kumar is a professor in M.R.I.U. His qualifications are as mentioned. Ph.D. (Computer Science & Engg.), UGC NET(Computer Science & Engg), M.Tech.( Computer Science & Engg.), B.Tech. (Computer Science & Engg.) He has 14 years of teaching experience and his areas of interest include Networking, Operating systems, Database management system. Total number of research publications are 31.](https://image.slidesharecdn.com/115feb177nov16574-899-1-smeditari-210608024538/75/Routing-in-Networks-using-Genetic-Algorithm-11-2048.jpg)