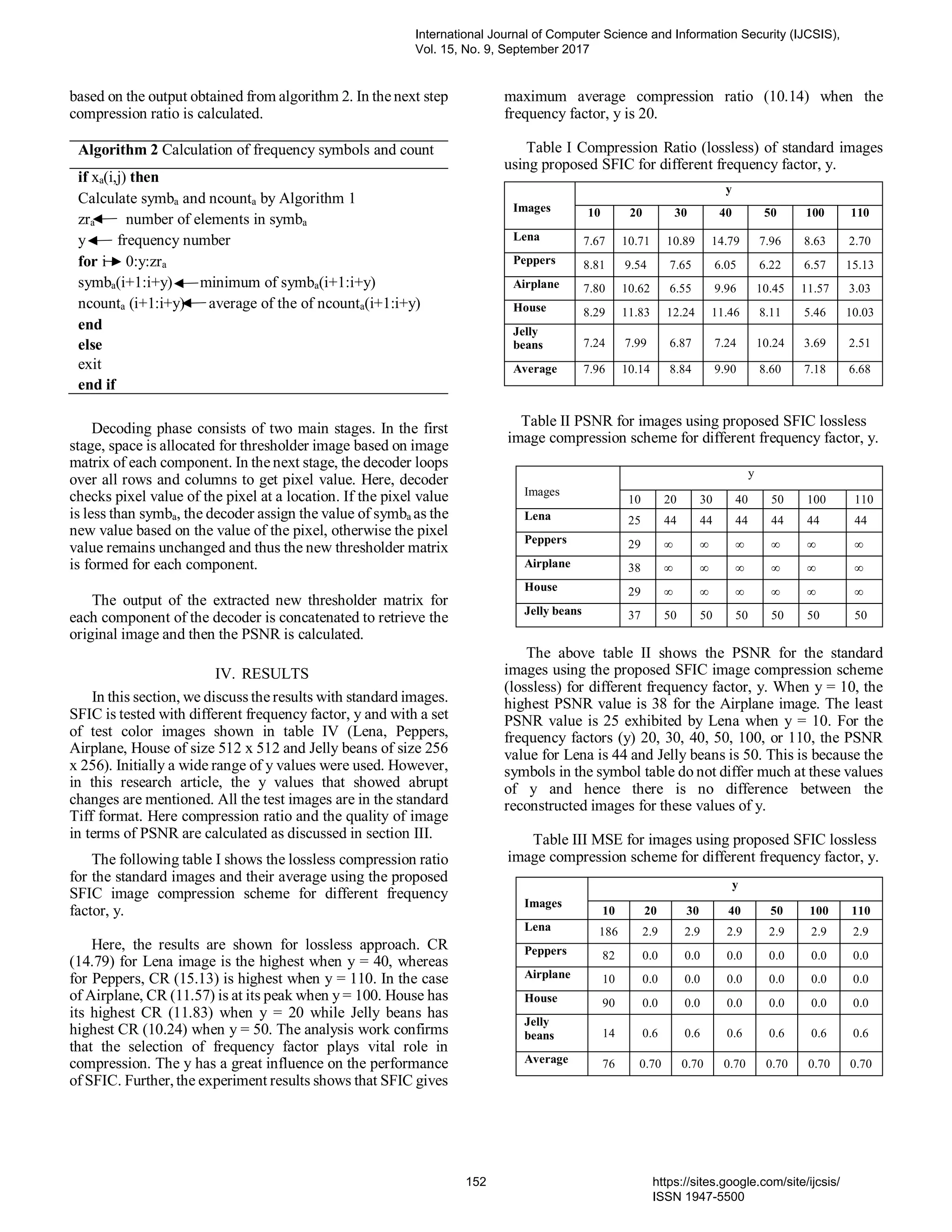
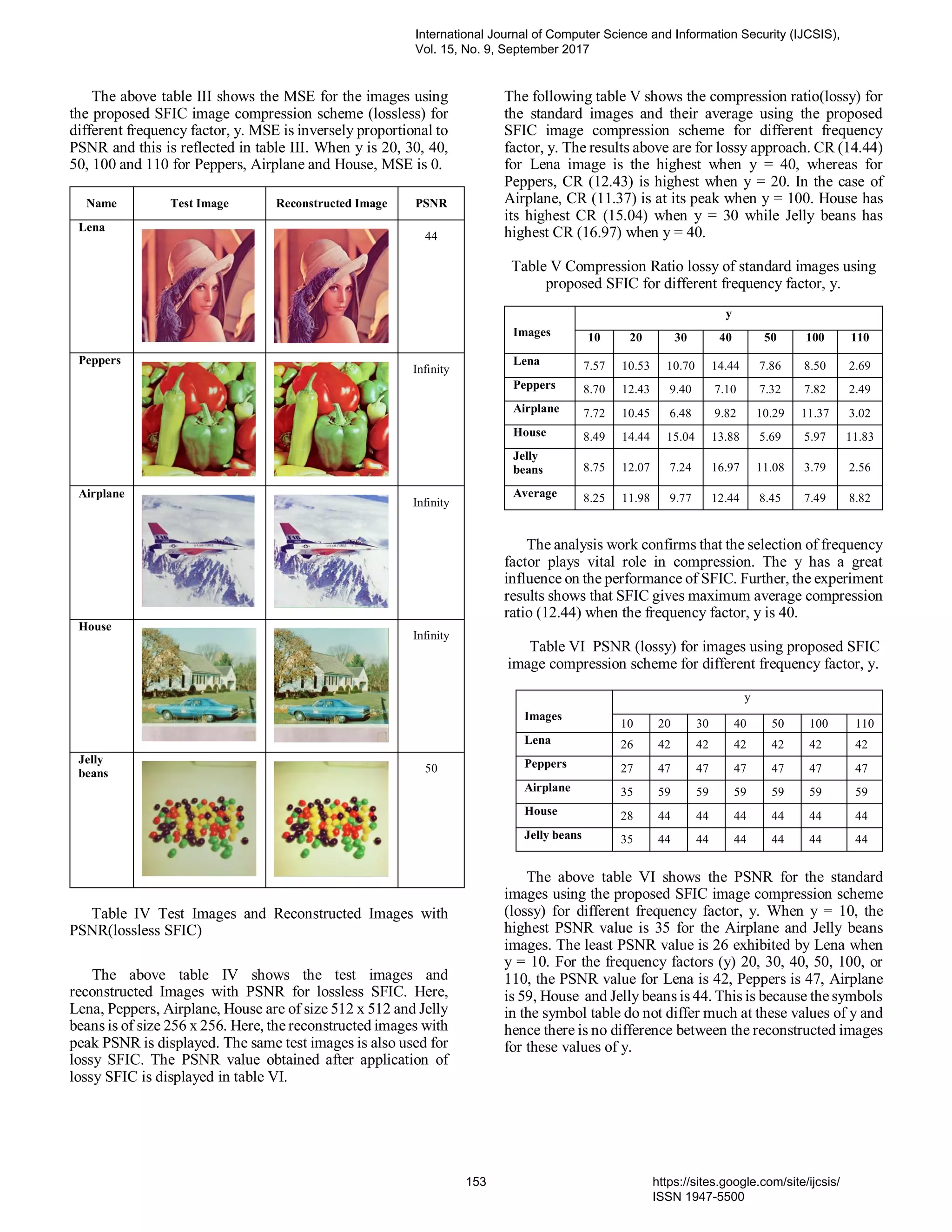
This document presents a new image compression technique called symbols frequency based image coding (SFIC), which reduces image size by utilizing the frequency of pixel values. The method merges pixel values within a frequency factor range to lower the total pixel count, leading to higher compression ratios and improved peak signal-to-noise ratios (PSNR). Experimental results demonstrate that this technique outperforms existing methods like quadtree-segmented AMBTC with bitmap omission for both lossy and lossless compression applications.
![Symbols Frequency based Image Coding for Compression Thafseela Koya Poolakkachalil PhD Scholar National Institute of Technology Durgapur, India thafseelariyas@hotmail.com Saravanan Chandran National Institute of Technology Durgapur, India dr.cs1973@gmail.com Vijayalakshmi K. Caledonian College of Engineering, Oman vijayalakshmi@caledonian.edu.om Abstract— The main aim of image compression is to represent the image with minimum number of bits and thus reduce the size of the image. This paper presents a Symbols Frequency based Image Coding (SFIC) technique for image compression. This method utilizes the frequency of occurrence of pixels in an image. A frequency factor, y is used to merge y pixel values that are in the same range. In this approach, the pixel values of the image that are within the frequency factor, y range are clubbed to the least pixel value in the set. As a result, there is omission of larger pixel values and hence the total size of the image reduces and thus results in higher compression ratio. It is noticed that the selection of the frequency factor, y has a great influence on the performance of the proposed scheme. However, higher PSNR values are obtained since the omitted pixels are mapped to pixels in the similar range. The proposed approach is analyzed with quantization and without quantization. The results are analyzed. This proposed new compression model is compared with Quadtree-segmented AMBTC with Bit Map Omission. From the experimental analysis it is observed that the proposed SFIC image compression scheme with both lossless and lossy techniques outperforms AMBTC-QTBO. Hence, the proposed new compression model is a better choice for lossless and lossy compression applications. Keywords- image compression, lossy compression, lossless compression, compression ratio, PSNR, MSE, probability. I. INTRODUCTION It has been observed that there is an escalation in the use of digital images for multimedia applications in the recent years. Over the past few years Internet based applications such as WhatsApp, Facebook, Twitter, several other social apps, and websites have been influencing usage of images and videos enormously. Initially, the focus of the users of these applications was on chats and text messages. However, there is a recent shift on the mode of usage of these applications from chats to sharing information in the form of digital images and videos. An uncompressed image consumes lot of storage and internet bandwidth. Hence, compression of digital images reduces the size of the image and occupies less storage and consumes less bandwidth. Digital image compression has been the subject of research for several decades. However, there has been focus on color image compression research work due to the immense amount of digital transmission of images through various internet based applications [1]-[2]. The idea of image compression is to represent the image with the smallest number of bits while maintaining the essential information in the image. The compression is achieved by exploiting the spatial and temporal redundancies. Advances in wavelet transform and quantization has produced algorithms that outperform image compression standards. The three main concepts that sets limit for image compression technique are image complexity, desired quality, and computational cost. The visual efficiency of an image compression technique depends directly on the amount of visually significant information it retains [3]- [4]. Image compression is classified as lossless image compression and lossy image compression based on whether the reproduced image pixels values are same or different respectively. Several research works has focused on lossy image compression focusing on Internet based applications [5]. However, medical image compression schemes prefer lossless technique, where each pixel value is vital. Other application of lossless image compression techniques include professional photography, application of computer vision analysis on recordings, automotive applications, input for post processing in digital camera, scientific and artistic images [6]- [7]. Algorithms used for lossless image compression include lossless JPEG [8], lossless Joint Photographic Experts Group (JPEG-LS) [9], LOCO-I [10], CALIC [11], JPEG2000 (lossless mode) [12] and JPEG XR [13]. However, these algorithms provide a small compression ratio compared with lossy compression as only information redundancy is removed while perceptual redundancy remains intact [14]- [15]. Lossy schemes provide much higher compression ratios than lossless schemes. However, the high image compression ratio obtained in lossy compression method is at the cost of the image quality. By lossy compression technique, the reconstructed image is not identical to the original image, but equitably close to it [16]. Color image processing is gaining importance due to the significant use of digital images over the Internet [17]. Since number of bits required to represent a color is three to four times more than the representation of grey levels, data compression plays a central role in the storage and transmission of color images [18]. It is an important technique for reducing the communication bandwidth consumption. It is highly useful in congested network like Internet or wireless multimedia transmission where there is low bandwidth. There International Journal of Computer Science and Information Security (IJCSIS), Vol. 15, No. 9, September 2017 148 https://sites.google.com/site/ijcsis/ ISSN 1947-5500](https://image.slidesharecdn.com/18paper31081741ijcsiscamerareadypp-180206144431/75/Symbols-Frequency-based-Image-Coding-for-Compression-1-2048.jpg)
![are various techniques for the compression of color images. In color image compression, the color components are separated by color transform. Each of the transformed components is independently compressed [19]. In this research article, compression ratio of the proposed new compression model for lossless and lossy compression techniques is analyzed. II. RELATED WORKS Jong et al. proposed a novel coding scheme for block truncation based on vector quantizer for color image compression in LCD overdrive. Experimental results showed that the proposed scheme achieved higher compression ratio and better visual quality when compared with conventional methods. This method is suitable for the hardware implementation in LCD overdrive due to the constant output bit-rate and the low computational complexity [20]. Banierbah and Khamadja proposed a novel approach that reduced the inter-band correlation by compensating the differences between them [21]. The prediction error was spatially coded by another method. This method had two main advantages namely: simplicity in implementation and application over parallel architectures. The comparison of this technique with various other techniques proved that this technique is very efficient and can even outperform them. This technique is applied for lossless, lossy, and scalable coding. This approach has provided motivation for research on lossless and lossy compression. Olivier et al. proposed a coding scheme in two layers. In the first layer, the image was compressed at low bit rates even while preserving the overall information and contours. The second layer encoded local texture in comparison to the initial partition [22]. This has given the motivation to target for higher PSNR values while obtaining high compression ratio. Min-Jen Tsai proposed a compression scheme for color images based on stack run coding. The highlight of this scheme was that a small number of symbol set was used to convert images from the wavelet transform domain to the compact data structure. The approach provided competitive PSNR values and high quality images at the same compression ratio when compared with other techniques [19]. This gave motivation to focus on compression technique which gives high compression ratio and good PSNR value with high quality reconstructed image at the same time. Soo et al. proposed an algorithm to train the color images based on Kohonen neural network for limited color displays. It was observed that the Peak Signal-to-Noise Ratio (PSNR) of the decoded image was high and that a good compression ratio could be obtained [23]. Experimental results showed that this method produced an average compression ratio of 13.09 and average Signal-to-Noise Ratio (SNR) of 30.69 [24].This has motivated to achieve higher compression ratio and SNR. Chen et al. proposed a color image compression scheme based on moment-preserving and block truncation coding where the input image is divided into non-overlapping blocks. Here, the average compression ratio was achieved 14.00 [24]. This idea inspired to include block truncation during quantization process of the proposed method. Panos and Rabab proposed A High-Quality fixed-Length Compression Scheme for Color Images where the Discrete Cosine Transform (DCT) of 8x8 picture blocks of an image was compressed by a fixed-length codewords. Fixed length encoding scheme was simpler to implement when compared to variable-length encoding scheme. This scheme was not susceptible to the error propagation and synchronization problems that were a part of variable-length coding schemes [25]. This has shown direction to incorporate DCT based application of the proposed approach in future work. Jinlei Zhang et al. propsed a novel coding scheme for the compression of hyperspectral images. The approach designed a distributive coding scheme that fulfilled the exclusive requirements of these images that includes lossless compression, progressive transmission, and low complexity onboard processing. Here, the complexity of data decorrelation was shifted to the decoder side to achieve lightweight onboard processing after image acquisition. The experimental results clearly demonstrated that this scheme achieved high compression ratio for lossless compression of HS images with a low complexity encoder [26]. This motivated to focus on research based on low complexity encoder. Pascal Peter proposed a new approach where a missing link between the discrete colorization of Levin et al. [27] and continuous diffusion-based inpainting in the YCbCr color space was introduced. With the proposed colorization technique, it was possible for the high-quality reconstruction of color data. This motivated to include pixel replacement technique in this paper based on the frequency of occurrence of the pixels exploiting the fact that the human eyes are more sensitive to structural information than color information [28]. Kim, Han Tai and Kim proposed the salient region detection via high–dimensional color transform and local special support which is a novel approach to automatically detect salient regions in an image. The approach consisted of the local and global features which complemented each other in the computation of the saliency map. The first step in the formation of formation of the saliency map was using a linear combination of colors in a high-dimensional color space. This observation is based on the fact that salient regions often possess distinctive features when compared to backgrounds in human perception. Human perception is nonlinear. The authors have shown the composition of accurate saliency map by finding the optimal linear combination of color coefficients in the high-dimensional color space. This is performed by mapping the low-dimensional red, green, and blue color to a feature vector in a high-dimensional color space. The second step was to utilize relative location and color contrast between superpixels as features and then to resolve the saliency estimation from a trimap via learning based algorithm. This step further improved the performance of the saliency estimation. It is observed that the additional local features and International Journal of Computer Science and Information Security (IJCSIS), Vol. 15, No. 9, September 2017 149 https://sites.google.com/site/ijcsis/ ISSN 1947-5500](https://image.slidesharecdn.com/18paper31081741ijcsiscamerareadypp-180206144431/75/Symbols-Frequency-based-Image-Coding-for-Compression-2-2048.jpg)
![learning based algorithm complement the global estimation from the high-dimensional color transform-based algorithm. The experimental results showed that this approach is effective in comparison with the previous state-of-art saliency estimation methods [29]. This motivated to utilize location of pixels and their pixel values. Rushi Lan et al. have proposed a local quaternion local ranking binary pattern (QLRBP) for color images. This method is different from the traditional descriptors where they are extracted from each color channel separately or from vector representations. QLRBP works on the quaternionic representation (QR) of the color image which encodes a color pixel using quaternion. QLRBP is able to handle all color channels directly in the quaternionic domain and include their dimensions simultaneously. QLRBP uses a reference quaternion to rank QRs of two color pixels, and performs a local binary coding on the phase of the transformed result to generate local descriptors of the color image. Experiments demonstrate that the QLRBP outperforms several state-of-art methods [30]. This motivated to club the color channels together while reconstructing the image. Yu-Chen Fan et al. proposed a luminance and color correction scheme for multiview image compression for a 3- DTV system. A 3-D discrete cosine transform (3-D DCT) based on cubic memory was proposed for image compression according to the characteristics of luminance and chrominance. After designing, the chip could achieve the goal. This method provided a solution for 3-D multiview compression and storage research and compression [31]. Seyum and Nam proposed the Hierarchical Prediction and context Adaptive Coding for Lossless Color Image Compression where the correlation between the pixels of an RGB image was removed by a color transform that was reversible. A conventional lossless image coder was used to compress luminance channel Y. Hierarchical decomposition and directional prediction was used for analyzing the pixels in the chrominance channel. In the later stage, arithmetic coding was applied to the prediction residuals. From the results, it was observed that the average bit rate reductions over JPEG2000 for Kodak image set, some medical images, and digital camera images were 7.105%, 13.55%, and 5.52% respectively [7]. This motivated to split the color channels in the beginning. Jose et al. proposed logarithmical hoping encoding algorithm which used Weber-Fechner law to encode the error between color component predictions and the actual values. Experimental results showed that this algorithm is suitable for static images based on adaptive logarithmical quantization [4]. This motivated to do future research work where the error between the replaced color component and the actual values can be estimated. Wu-Lin et al. proposed a novel color image compression technique based on block truncation where quadtree segmentation technique was employed to partition the color image. Experimental results showed that the proposed approach cuts down the bit rates significantly while keeping good quality for the reconstructed image [1]. This motivated to direct the research in a way that high quality images are obtained at minimum bit rates. Mohamed et al. proposed a lossless image compression technique where the prediction step was combined with the integer wavelet transform. Experimental results showed that this technique provided higher compression ratios than competing techniques [14]. Wu-Lin Chen et al. proposed the Quadtree-segmented AMBTC with Bit Map Omission (AMBTC-QTBO) [1]. In this approach the color image is decomposed into three grayscale images. Then each grayscale image is partitioned into a set of variable-sized blocks using quadtree segmentation. The algorithm for AMBTC-QTBO is as follows: 1. Decompose color image into three grayscale images 2. Partition grayscale images to 16x16 non overlapping block sets 3. Compute the block means and two quantization levels a, b using AMBTC [32] for each block. 4. If|a − b| ≤ 𝑇𝐻𝑄𝑇, encode 16x16 block using its block mean and go to 8. Otherwise, divide this block into 8x8 equal-size pixel blocks. 5. Calculate block mean and two level quantization for 8x8 blocks. 6. If|a − b| ≤ 𝑇𝐻𝐵𝑂, encode 8x8 block using its block mean and go to 8. Otherwise, divide this block into 4x4 equal-size pixel blocks. 7. Calculate block mean and two level quantization for 4x4 blocks. If|a − b| ≤ 𝑇𝐻𝐵𝑂, encode 4x4 block using its block mean and go to 8. Otherwise, encode 4x4 block by AMBTC. 8. Go to 3 if there are any blocks to be processed. In the above algorithm, the predefined threshold THQT is used to determine whether the grayscale image blocks are to be further subdivided. Adding to the above, another pre- defined threshold THBO is used to determine the block activity for 4x4 image blocks in the bit map omission technique. In order to perform performance comparison, the proposed method in this paper has been compared with AMBTC-QTBO. The aim of this research article is to propose a novel compression scheme for image namely, Symbols Frequency based Image Coding (SFIC) for Color Image Compression. The following Section III describes the proposed SFIC compression technique. The following Section IV Experiments and Results, analyses the proposed SFIC with lossless and lossy conditions and Quadtree-segmented AMBTC with Bit Map Omission [1]. Standard images are used in this experiment. Conclusions are drawn in section V. III. IMAGE COMPRESSION Two essential criteria that are used to measure the performance of a compression scheme are: Compression International Journal of Computer Science and Information Security (IJCSIS), Vol. 15, No. 9, September 2017 150 https://sites.google.com/site/ijcsis/ ISSN 1947-5500](https://image.slidesharecdn.com/18paper31081741ijcsiscamerareadypp-180206144431/75/Symbols-Frequency-based-Image-Coding-for-Compression-3-2048.jpg)
![Ratio (CR) and Peak Signal to Noise Ratio (PSNR), which is the measurement of the quality of the reconstructed image. a) Compression Ratio The Compression Ratio (CR) is defined as the ratio between the size of the original image (n1) and the size of the compressed image (n2) [33]. 𝐶𝑅 = 𝑛1/𝑛2 b) Peak Signal to Noise Ratio PSNR is an expression for the ratio between the maximum possible value (power) of a signal and the power of distorting noise that affects the quality of its representation [34]. The mathematical representation of the PSNR is as follows: where the MSE (Mean Squared Error) is: The three basic steps in the compression of still images are transformation, quantization and encoding. During the transformation step, the data set is transformed into another equivalent data set by the mapper. During the quantization phase, the quantizer reduces the precision of the mapped data set in agreement with a previously recognized reliability criterion. In the quantization process, scaling of data set by quantization factor takes place whereas in thresholding, all trivial samples are eliminated. These two processes are responsible for the introduction of data loss and degradation of quality. The overall number of bits required to represent the data set is reduced in the encoding phase [2]- [35]. In lossless compression, the quantization step is eliminated since it introduces quantization errors that inhibit the perfect reconstruction of the image. The quantization step is usually used to turn the transformation coefficients from their float format to an integer format [14]. In the case of lossless compression, most color transforms are not used due to their un-invertibility with integer arithmetic. As a result, invertible version of color transform, the Revertible Color Transform (RCT) is used in JPEG2000 [12]. In the case of lossy compression, since all trivial samples are eliminated during quantization, higher compression ratios are obtained when compared to lossless compression, but at the cost of poor quality of the reconstructed image. A. Proposed SFIC Encoding Scheme In this section, we explain the new compression model SFIC that utilizes the pixel values that are in the same range. The block diagram of the SFIC is displayed in following figure 1. First, the image is transformed into a matrix. Further, the R, G, B components (xa(i,j)) of the image is extracted. In SFIC, pixel values of the R, G, and B components in the integer format are not converted to YCbCr. This is eliminated as the reverse conversion from float to integer values is not taking place. In the next step, the encoding takes place. There are three stages in the encoder. In the first stage, the pixel values, hereafter named as symba and their frequency of occurrence in each component, hereafter named as ncounta is calculated. symba and ncounta of pixels in each component is obtained using algorithm 1. In algorithm 1, xa(i,j) , the R,G,B components of the image is used as the input and seq_vectora, which is the column wise representation of xa(i,j) is found. In the next step, the pixel values are sorted and stored in symba.This is found by extracting the minimum to maximum values of pixels in seq_vectora. In the next step of algorithm 1, the frequency of occurrence of each pixel in symba is obtained by histogram analysis and is stored as ncounta. The overall frequency based coding scheme takes place in algorithm 2, which is summarized as below. Fig. 1: Block Diagram of proposed SFIC In algorithm 2, a frequency factor, y is used to merge y pixel values. For each of the y symba which are already in ascending order, the minimum pixel value among the y symba is made as the new pixel value. The average ncounta of the y pixels is made as the new ncounta. These steps in algorithm 2 result in the reduction of number of distinct pixels. In the third stage of the encoder, unique symbols and count are extracted Algorithm 1 Calculation of symbols and count if xa(i,j) then seq_vectora [xa(i,j) (:)]' symba minimum to maximum of seq_vectora ncounta histogram bin values of symba else exit end if (3) (2) (1) International Journal of Computer Science and Information Security (IJCSIS), Vol. 15, No. 9, September 2017 151 https://sites.google.com/site/ijcsis/ ISSN 1947-5500](https://image.slidesharecdn.com/18paper31081741ijcsiscamerareadypp-180206144431/75/Symbols-Frequency-based-Image-Coding-for-Compression-4-2048.jpg)
![Table VII Comparison of Compression Ratio (CR), PSNR of SFIC and AMBTC-QTBO. In the above table VII, the proposed image coding scheme (lossless and lossy technique) is compared with Quadtree- segmented AMBTC with Bit Map Omission (AMBTC- QTBO) and the results are analyzed. The average CR using SFIC in lossless scheme is 10.68, whereas with lossy scheme is 11.31. This increase in CR is due to the presence of quantization step in lossy scheme. In the case of AMBTC- QTBO, the average CR is 5.32. These results indicate that the CR obtained by proposed lossless and lossy scheme is more than twice the CR obtained by AMBTC-QTBO. The average PSNR value with SFIC in lossless scheme is infinity whereas with SFIC in lossy scheme is 48. The reduction in the PSNR value in the case of lossy scheme is justifiable as there is loss of data due to quantization in the reconstructed image. In the case of AMBTC- QTBO, PSNR is 32. This is far less than the PSNR obtained by SFIC in both lossless and lossy scheme. From the analysis it is seen that SFIC image compression scheme with lossless and lossy techniques outperforms AMBTC- QTBO. V. CONCLUSION In this research article, a novel approach for image compression based on the probability of the frequency of occurrence of pixels has been proposed. This method is compared with the Quadtree-segmented AMBTC with Bit Map Omission. The average CR with SFIC in lossless scheme is 10.68, whereas with lossy scheme is 11.31. This increase in CR is due to the presence of quantization step in lossy scheme. This means that SFIC with lossless and lossy scheme provides 50% better color image compression than AMBTC- QTBO. SFIC in both lossless and lossy schemes also produced higher PSNR than AMBTC-QTBO showing better picture quality for the regenerated image. From the analysis it is seen that SFIC image compression scheme with lossless and lossy techniques outperforms AMBTC- QTBO. Hence SFIC is applicable is a better choice for lossless and lossy applications. For example, SFIC approach with lossless technique is applicable in medical, scientific, and artistic images. SFIC approach with lossy technique is applicable for WhatsApp, Facebook, Twitter and other social media apps and websites. REFERENCES [1] W. L. Chen, Y. C. Hu, K. Y. Liu, C. C. Lo and C. H. Wen, "Variable- Rate Quadtree-segmented Block Truncation Coding for Color Image Compression," International Journal of Signal Processing, Image Processing and Pattern Recognition, vol. VII, no. 1, pp. 65-76, 2014. [2] G. K. Kharate and V. H. Patil, "Color Image Compression Based On Wavelet Packet Best Tree," IJCSI International Journal of Computer Science Issues, vol. III, no. 2, pp. 31-35, 2010. [3] M. J. Nadenau, J. Reichel and M. Kunt, "Wavelet-Based Color Image Compression: Exploiting the Contrast Sensitivity Function," IEEE Transactions on Image Processing, vol. XII, no. 1, pp. 58-70, 2003. [4] J. J. Garcia Aranda, M. G. Casquete, M. C. Cueto, J. N. Salmeron and F. G. Vidal, "Logarithmical Hopping Encoding: A Low Computational Complexity Algorithm for Image Compression," IET Image Processing, vol. IX, no. 8, pp. 643-651, 2014. [5] C. San Jose, "Requirements for An Extension of HEVC for Coding of Screen Content, document N14174". USA Patent ISO/IEC JTC 1/SC 29/WG 11,, January 2014. [6] A. Weinlich, P. Amon, A. Hutter and A. Kaup, "Probability Distribution Estimation for Autoregressive Pixel-Predictive Image Coding," IEEE Transactions on Image Processing, vol. XXV, no. 3, pp. 1382-1395, 2016. [7] S. Kim and N. I. Cho, "Hierarchical Prediction and context Adaptive Coding for Lossless Color Image Compression," IEEE Transactions on Image Processing, vol. XXIII, no. 1, pp. 445-449, 2014. [8] W. B. Pennebaker and J. L. Mitchell, "JPEG Still Image Data Compression Standard," Van Nostrand Reinhold, 1993. [9] "ISO/IEC Standard 14495-1," Information Technology—Lossless and Near-Lossless Compression of Continuous-Tone Still Images (JPEG- LS), April 1999. [10] . M. Weinberger, . G. Seroussi and G. Sapiro, "The LOCO-I lossless image compression algorithm: Principles and standardization into JPEG-LS," IEEE Transactions on Image Processing, vol. IX, no. 8, p. 1309–1324, 2000. [11] . X. Wu and N. Memon, "Context-based, adaptive, lossless image coding," IEEE Transactions on Communications, vol. XLV, no. 4, p. 437–444, 1997. [12] "Information Technology—JPEG 2000 Image Coding System—Part 1: Core Coding System," INCITS/ISO/IEC Standard 15444-1, 2000. [13] "ITU-T and ISO/IEC, JPEG XR Image Coding System—Part 2: Image Coding Specification," ISO/IEC Standard 29199-2, 2011. [14] M. M. Fouad and R. M. Dansereau, "Lossless Image Compression Using A Simplified MED Algorithm with Integer Wavelet Transform," I.J. Image, Graphics and Signal Processing, vol. 1, pp. 18-23, 2014. [15] W. J. Weinberger, G. Seroussi and G. Sapiro, "The LOCO-I Lossless Image Compression Algorithm: Principles and standardization into JPEG-LS," IEEE Transactions on Image Processing, vol. IX, no. 8, pp. 1309-1324, 2000. [16] S. Aggrawal and P. l. Srivastava, "Overview of Image Compression Techniques," Journal of Computer Programming and Multimedia, vol. 1, no. 2, 2016. [17] R. C. Gonzalez and R. E. Woods, Digital Image Processing, Pearson Education, 2016, p. 27. [18] R. C. Gonzalez and R. E. Woods, Digital Image Processing, Pearson India Education Services Pvt.Ltd, 2016, p. 454. [19] M. T. Tsai, "Very Low Bit Rate Color Image Compression by Using Stack-Run-End-Coding," IEEE Transactions on Consumer Electronics, vol. XLVI, no. 2, pp. 368-374, 2000. [20] J. W. Han, M. C. hwang, S. G. Kim, T. H. You and S. J. Ko, "Vector Quantizer based Block Truncation Coding for Color Image Compression in LCD Overdrive," IEEE Transactions on Consumer electronics, vol. LIV, no. 4, pp. 1839-1845, 2008. Image SFIC CR Lossless SFIC CR Lossy AMBTC CR SFIC PSNR Lossless SFIC PSNR Lossy AMBTC PSNR Lena 10.71 14.44 5.99 44 42 33 Peppers 9.54 7.10 6.02 ∞ 47 32 Airplane 10.62 9.82 4.17 ∞ 59 32 House 11.83 13.88 5.10 ∞ 44 30 Average 10.68 11.31 5.32 ∞ 48 32 International Journal of Computer Science and Information Security (IJCSIS), Vol. 15, No. 9, September 2017 154 https://sites.google.com/site/ijcsis/ ISSN 1947-5500](https://image.slidesharecdn.com/18paper31081741ijcsiscamerareadypp-180206144431/75/Symbols-Frequency-based-Image-Coding-for-Compression-7-2048.jpg)
![[21] S. Benierbah and M. Khamadja, "Compression of Colour Images by Inter-band Compensated Prediction," IEE Proceedings - Vision, Image and Signal Processing, vol. CLIII, no. 2, pp. 237-243, 2006. [22] O. Deforges, M. Babel, L. Bedat and J. Ronsin, "Color LAR Codec: A Color Image representation and Compression Scheme Based on Local Resolution Adjustment and self-Extracting Region representation," IEEE Transactions on Circuits and Systems for Video Technology, vol. XVII, no. 8, pp. 974-987, 2007. [23] S. C. Pei and Y. S. Lo, "Color Image Compression and Limited Display Using Self-organization Kohonen Map," IEEE Transactions on Circuits and Systems for Video Technology, vol. VIII, no. 2, pp. 191-205, 1998. [24] C. K. Yang, J. C. Lin and W. H. Tsai, "Color Image Compression by Moment-Preserving and Block Truncation Coding Techniques," IEEE Transactions On Communications, vol. XLV, no. 12, pp. 1513-1516, 1997. [25] p. Nasiopoulos and R. K. Ward, "A High-Quality fixed-Length Compression Scheme for Color Images," IEEE Transactions on Communications, vol. XLIII, no. 11, pp. 2672-2677, 1995. [26] J. Zhang, H. Li and C. W. Chen, "Distributed Lossless Coding Techniques for Hyperspectral Images," IEEE Journal of Selected Topics in Signal Processing, vol. IX, no. 6, pp. 977-989, 2015. [27] A. Levin, D. Lischinski and Y. Weiss, "Colorization using Optimization," CM Transactions on Graphics, vol. XXIII, 2004. [28] P. Peter, L. Kaufhold and J. Weickert, "Turning Diffusion-based Image Colorization into Efficient Color Compression," IEEE Transactions on Image Processing, vol. XXVI, no. 2, 2017. [29] J. Kim, D. Han, Y. W. Tai and K. Junmo, "Salient Region Detection via High-Dimensional Color Transform and Local Spatial Support," IEEE Transactions on Image Processing, vol. XXV, no. 1, pp. 9-23, 2016. [30] R. Lan, Y. Zhou and Y. Y. Tang, "Quaternionic Local Ranking Binary Pattern: A Local Descriptor of Color Images," IEEE Transactions on Image Processing, vol. XXV, no. 2, pp. 566-579, February 2016. [31] Y. C. Fan, J. L. You, J. H. Shen and C. Hung, "Luminance and Color Correction of Multiview Image compression for 3-DTV System," IEEE Transactions on Magnetics, vol. L, no. 7, July 2014. [32] D. Halverson, N. Griswold and G. Wise, "A Generalized Block truncation Coding Algorithm for Image Compression," IEEE Transactions on Acoustics Speech Signal Processing, vol. XXXII, no. 3, pp. 664-668, 1984. [33] A. M. Raid, W. M. Khedr, M. A. El-dosuky and W. Ahmed, "JPEG Image Compression Using Discrete Cosine Transform - A Survey," International Journal of Computer Science &Engineering, vol. V, no. 2, pp. 39-47, 2014. [34] [Online]. Available: http://www.ni.com/white-paper/13306/en/. [Accessed 18 August 2017]. [35] R. C. Gonzalez and R. E. Woods, Digital Image Processing, Pearson India Education Pvt. Ltd, 2016, pp. 536-537. [36] U. Bayazit, "Adaptive Spectral Transform for Wavelet-Based Color Image Compression," IEEE Transactions on Circuits and Systems for Video Technology, vol. XXI, no. 7, pp. 983-992, 2011. International Journal of Computer Science and Information Security (IJCSIS), Vol. 15, No. 9, September 2017 155 https://sites.google.com/site/ijcsis/ ISSN 1947-5500](https://image.slidesharecdn.com/18paper31081741ijcsiscamerareadypp-180206144431/75/Symbols-Frequency-based-Image-Coding-for-Compression-8-2048.jpg)