Sylvester's sequence

Question

Sylvester's sequence, OEIS A000058, is an integer sequence defined as follows:

Each member is the product of all previous members plus one. The first member of the sequence is 2.

Task

Create a program to calculate the nth term of Sylvester's Sequence. Standard input, output and loopholes apply.

Standard sequence rules apply.

This is code-golf, so the goal is to minimize the size of your source code as measured in bytes.

Test Cases

You may use either zero or one indexing. (Here I use zero indexing)

>>0 2 >>1 3 >>2 7 >>3 43 >>4 1807

What inputs are expected to be handled? The output grows quite rapidly. — Geobits
– Geobits, Commented Aug 26, 2016 at 1:44
@Geobits you are expected to handle as much as your language can — Wheat Wizard
– Wheat Wizard ♦, Commented Aug 26, 2016 at 1:46
TypeScript’s type system can handle unary numbers up to 999, but could also take the input as a list of base-10 digits and do math in those, but for many more bytes. Would the first be acceptable, or must I choose the second since it’s possible? — noodle person
– noodle person, Commented Sep 16, 2023 at 21:16

caird coinheringaahing · Accepted Answer · 2022-10-14 22:39:11Z

Brain-Flak, 76 68 58 52 46 bytes

<>(()())<>{({}[()])<>({({}[()])({})}{}())<>}<>

Try it online!

Uses this relationship instead:

$$a(n) = 1+\sum^{a(n-1)-1}_{i=0} 2i$$

which is derived from this relationship modified from that provided in the sequence:

$$a(n+1) = a(n)(a(n) - 1) + 1.$$

Explanation

For a documentation of what each command does, please visit the GitHub page.

There are two stacks in Brain-Flak, which I shall name as Stack 1 and Stack 2 respectively.

The input is stored in Stack 1.

<>(()())<> Store 2 in Stack 2. { while(Stack_1 != 0){ ({}[()]) Stack_1 <- Stack_1 - 1; <> Switch stack. ({({}[()])({})}{}()) Generate the next number in Stack 2. <> Switch back to Stack 1. } <> Switch to Stack 2, implicitly print.

For the generation algorithm:

({({}[()])({})}{}()) Top <- (Top + Top + (Top-1) + (Top-1) + ... + 0) + 1 ( ) Push the sum of the numbers evaluated in the process: { } while(Top != 0){ ({}[()]) Pop Top, push Top-1 (added to sum) ({}) Pop again, push again (added to sum) } {} Top of stack is now zero, pop it. () Evaluates to 1 (added to sum).

Alternative 46-byte version

This uses only one stack.

({}<(()())>){({}<({({}[()])({})}{}())>[()])}{}

Try it online!

Only 10 more bytes to show that java develepors should go to brain flack — Rohan Jhunjhunwala
– Rohan Jhunjhunwala, Commented Aug 26, 2016 at 3:15
@LeakyNun it still is interesting to think of. Brain Flak has some power, and is suprisingly terse — Rohan Jhunjhunwala
– Rohan Jhunjhunwala, Commented Aug 26, 2016 at 3:21
The one stack version is also stack clean. Which tends to be a important point for code modularity in brain-flak. — Wheat Wizard
– Wheat Wizard ♦, Commented Aug 26, 2016 at 4:51

Dennis · Accepted Answer · 2016-08-26 03:47:22Z

Jelly, 5 bytes

Ḷß€P‘

This uses 0-based indexing and the definition from the challenge spec.

Try it online! or verify all test cases.

How it works

Ḷß€P‘ Main link. Argument: n Ḷ Unlength; yield [0, ..., n - 1]. ß€ Recursively apply the main link to each integer in that range. P Take the product. This yields 1 for an empty range. ‘ Increment.

\$\begingroup\$ Ah, I forgot that the empty product is 1. \$\endgroup\$

Leaky Nun
– Leaky Nun

2016-08-26 03:46:55 +00:00
Commented Aug 26, 2016 at 3:46 — Leaky Nun
– Leaky Nun, Commented Aug 26, 2016 at 3:46

Martin Ender · Accepted Answer · 2016-08-26 18:01:45Z

Hexagony, 27 bytes

1{?)=}&~".>")!@(</=+={"/>}*

Unfolded:

 1 { ? ) = } & ~ " . > " ) ! @ ( < / = + = { " / > } * . . . . . . . . . .

Try it online!

Explanation

Let's consider the sequence b(a) = a(n) - 1 and do a little rearranging:

b(a) = a(n) - 1 = a(n-1)*(a(n-1)-1) + 1 - 1 = (b(n-1) + 1)*(b(n-1) + 1 - 1) = (b(n-1) + 1)*b(n-1) = b(n-1)^2 + b(n-1)

This sequence is very similar but we can defer the increment to the very end, which happens to save a byte in this program.

So here is the annotated source code:

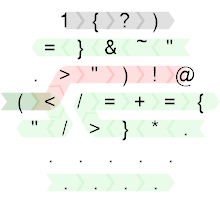
^{Created with Timwi's HexagonyColorer.}

And here is a memory diagram (the red triangle shows the memory pointer's initial position and orientation):

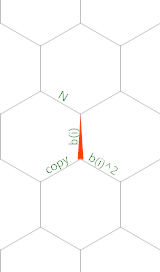
^{Created with Timwi's EsotericIDE.}

The code begins on the grey path which wraps the left corner, so the initial linear bit is the following:

1{?)( 1 Set edge b(1) to 1. { Move MP to edge N. ? Read input into edge N. )( Increment, decrement (no-op).

Then the code hits the < which is a branch and indicates the start (and end) of the main loop. As long as the N edge has a positive value, the green path will be executed. That path wraps around the grid a few times, but it's actually entirely linear:

""~&}=.*}=+={....(

The . are no-ops, so the actual code is:

""~&}=*}=+={( "" Move the MP to edge "copy". ~ Negate. This is to ensure that the value is negative so that &... & ...copies the left-hand neighbour, i.e. b(i). }= Move the MP to edge b(i)^2 and turn it around. * Multiply the two copies of b(i) to compute b(i)^2. }= Move the MP back to edge b(i) and turn it around. + Add the values in edges "copy" and b(i)^2 to compute b(i) + b(i)^2 = b(i+1). ={ Turn the memory pointer around and move to edge N. ( Decrement.

Once this decrementing reduces N to 0, the red path is executed:

")!@ " Move MP back to edge b(i) (which now holds b(N)). ) Increment to get a(N). ! Print as integer. @ Terminate the program.

@CalculatorFeline The brute forcer can do at most 7-byte programs (and even that only with a bunch of assumptions) in a reasonable amount of time. I don't see this being remotely possible in 7 bytes. — Martin Ender
– Martin Ender, Commented Jun 19, 2017 at 17:42
@CalculatorFeline Laziness. The brute forcer always requires a bit of manual tweaking that I can't be bothered to do for the practically 0 chance that it will find something. Some version of the script is on GitHub though so anyone else is free to give it a go. — Martin Ender
– Martin Ender, Commented Jun 19, 2017 at 17:48

Conor O'Brien · Accepted Answer · 2016-08-26 11:15:53Z

J, 18 14 12 bytes

This version thanks to randomra. I'll try to write a detailed explanation later.

0&(]*:-<:)2:

J, 14 bytes

This version thanks to miles. Used the power adverb ^: instead of an agenda as below. More explanation to come.

2(]*:-<:)^:[~]

J, 18 bytes

2:`(1+*/@$:@i.)@.*

0-indexed.

Examples

 e =: 2:`(1+*/@$:@i.)@.* e 1 3 e 2 7 e 3 43 e 4 1807 x: e i. 10 2 3 7 43 1807 3263443 10650056950807 113423713055421862298779648 12864938683278674737956996400574416174101565840293888 1655066473245199944217466828172807675196959605278049661438916426914992848 91480678309535880456026315554816 |: ,: x: e i. 10 2 3 7 43 1807 3263443 10650056950807 113423713055421862298779648 12864938683278674737956996400574416174101565840293888 165506647324519994421746682817280767519695960527804966143891642691499284891480678309535880456026315554816

Explanation

This is an agenda that looks like this:

 ┌─ 2: │ ┌─ 1 ┌───┤ ├─ + │ └────┤ ┌─ / ─── * ── @. ─┤ │ ┌─ @ ─┴─ $: │ └─ @ ─┴─ i. └─ *

(Generated using (9!:7)'┌┬┐├┼┤└┴┘│─' then 5!:4<'e')

Decomposing:

 ┌─ ... │ ── @. ─┤ │ └─ *

Using the top branch as a the gerund G, and the bottom as the selector F, this is:

e n <=> ((F n) { G) n

This uses the constant function 2: when 0 = * n, that is, when the sign is zero (thus n is zero). Otherwise, we use this fork:

 ┌─ 1 ├─ + ──┤ ┌─ / ─── * │ ┌─ @ ─┴─ $: └─ @ ─┴─ i.

Which is one plus the following atop series:

 ┌─ / ─── * ┌─ @ ─┴─ $: ── @ ─┴─ i.

Decomposing further, this is product (*/) over self-reference ($:) over range (i.).

You can also use the power adverb to get 2(]*:-<:)^:[~] for 14 bytes using the formula a(0) = 2 and a(n+1) = a(n)^2 - (a(n) - 1). To compute larger values, the 2 at the start will have to be marked as an extended integer. — miles
– miles, Commented Aug 26, 2016 at 4:08
Both solutions are very nice. I think I was unaware of the v`$:@.u recursive format. I always used a ^:v format which is often more complex. @miles I also never used the (]v) trick. It took me a good 5 minutes to understand it. — randomra
– randomra, Commented Aug 26, 2016 at 8:37
For completeness a 3rd kind of looping (14 bytes using miles's method): 2(]*:-<:)~&0~] (or 2:0&(]*:-<:)~]). And combining them 13 bytes ]0&(]*:-<:)2:. — randomra
– randomra, Commented Aug 26, 2016 at 8:44
12 bytes: 0&(]*:-<:)2:. (Sorry, I shouldn't golf in the comments.) — randomra
– randomra, Commented Aug 26, 2016 at 8:52
@randomra That is a really neat use of bond. I had to read the page to find out exactly what happened since normally one would think that middle verb was receiving three arguments. — miles
– miles, Commented Aug 26, 2016 at 10:20

Brad Gilbert b2gills · Accepted Answer · 2016-08-26 15:18:07Z

Perl 6, 24 bytes

{(2,{1+[*] @_}...*)[$_]}

{(2,{1+.²-$_}...*)[$_]}

Explanation

# bare block with implicit parameter ｢$_｣ { ( # You can replace 2 with 1 here # so that it uses 1 based indexing # rather than 0 based 2, # bare block with implicit parameter ｢@_｣ { 1 + # reduce the input of this inner block with ｢&infix:<*>｣ # ( the input is all of them generated when using a slurpy @ var ) [*] @_ # that is the same as: # ｢@_.reduce: &infix:<*>｣ } # keep calling that to generate more values until: ... # forever * # get the value as indexed by the input )[ $_ ] }

Usage:

my &code = {(2,{1+[*] @_}...*)[$_]} say code 0; # 2 say code 1; # 3 say code 2; # 7 say code 3; # 43 say code 4; # 1807 # you can even give it a range say code 4..7; # (1807 3263443 10650056950807 113423713055421844361000443) say code 8; # 12864938683278671740537145998360961546653259485195807 say code 9; # 165506647324519964198468195444439180017513152706377497841851388766535868639572406808911988131737645185443 say code 10; # 27392450308603031423410234291674686281194364367580914627947367941608692026226993634332118404582438634929548737283992369758487974306317730580753883429460344956410077034761330476016739454649828385541500213920807 my $start = now; # how many digits are there in the 20th value say chars code 20; # 213441 my $finish = now; # how long did it take to generate the values up to 20 say $finish - $start, ' seconds'; # 49.7069076 seconds

\$\begingroup\$ An array slice with $_? What witchcraft is this? \$\endgroup\$

Zaid
– Zaid

2016-08-26 16:15:15 +00:00
Commented Aug 26, 2016 at 16:15 — Zaid
– Zaid, Commented Aug 26, 2016 at 16:15

nimi · Accepted Answer · 2016-08-26 05:27:50Z

8

Haskell, 26 bytes

f n|n<1=2|m<-f$n-1=1+m*m-m

Usage example: f 4 -> 1807.

answered Aug 26, 2016 at 5:27

nimi

36k4 gold badges35 silver badges100 bronze badges

Add a comment |

Community · Accepted Answer · 2020-06-17 09:04:33Z

7

Java 7, 46 42 bytes

int f(int n){return--n<0?2:f(n)*~-f(n)+1;}

Uses 0-indexing with the usual formula. I swapped n*n-n for n*(n-1) though, since Java doesn't have a handy power operator, and the f() calls were getting long.

edited Jun 17, 2020 at 9:04

CommunityBot

1

answered Aug 26, 2016 at 2:21

Geobits

19.7k4 gold badges56 silver badges125 bronze badges

3

\$\begingroup\$ f(n)*~-f(n) should work. \$\endgroup\$

Dennis
– Dennis

2016-08-26 02:44:32 +00:00
Commented Aug 26, 2016 at 2:44
1

\$\begingroup\$ How do I forget about that trick every single time? If that isn't on the tips page, it's damn sure about to be. \$\endgroup\$

Geobits
– Geobits

2016-08-26 02:45:34 +00:00
Commented Aug 26, 2016 at 2:45
2

\$\begingroup\$ return--n<0 saves one more byte. \$\endgroup\$

Dennis
– Dennis

2016-08-26 02:49:40 +00:00
Commented Aug 26, 2016 at 2:49
2

\$\begingroup\$ But java developers should go to brain-flak anyway. \$\endgroup\$

Leaky Nun
– Leaky Nun

2016-08-26 03:23:51 +00:00
Commented Aug 26, 2016 at 3:23
3

\$\begingroup\$ @Leaky Nun If I can't simulate a simple die roll without rolling my own PRNG, I'm not a fan of it :P \$\endgroup\$

Geobits
– Geobits

2016-08-26 03:32:51 +00:00
Commented Aug 26, 2016 at 3:32

| Show 2 more comments

xnor · Accepted Answer · 2016-08-26 08:12:31Z

6

Haskell, 25 bytes

(iterate(\m->m*m-m+1)2!!)

answered Aug 26, 2016 at 8:12

xnor

150k26 gold badges287 silver badges676 bronze badges

Add a comment |

Community · Accepted Answer · 2017-04-13 12:38:59Z

6

S.I.L.O.S, 60 bytes

readIO p = 2 lblL r = p r + 1 p * r i - 1 if i L printInt r

Try it online!

Port of my answer in C.

edited Apr 13, 2017 at 12:38

CommunityBot

1

answered Aug 26, 2016 at 16:29

Leaky Nun

50.6k6 gold badges115 silver badges291 bronze badges

\$\begingroup\$ Yay :D finally a SILOS golfer, the interesting thing is that it beats Scala :) \$\endgroup\$

Rohan Jhunjhunwala
– Rohan Jhunjhunwala

2016-08-26 16:32:30 +00:00
Commented Aug 26, 2016 at 16:32

Add a comment |

emanresu A · Accepted Answer · 2021-06-03 12:23:18Z

6

Oasis, 4 bytes

Probably my last language from the golfing family! ~~Non-competing, since the language postdates the challenge.~~

Code:

²->2

Alternative solution thanks to Zwei:

<*>2

Expanded version:

a(n) = ²-> a(0) = 2

Explanation:

² # Stack is empty, so calculate a(n - 1) ** 2. - # Subtract, arity 2, so use a(n - 1). > # Increment by 1.

Uses the CP-1252 encoding. Try it online!

edited Jun 3, 2021 at 12:23

emanresu A

46.2k5 gold badges112 silver badges257 bronze badges

answered Aug 31, 2016 at 0:56

Adnan

44.7k6 gold badges83 silver badges248 bronze badges

\$\begingroup\$ Last golfing language? You're not going to make any more? D: \$\endgroup\$

Conor O'Brien
– Conor O'Brien

2016-08-31 00:58:22 +00:00
Commented Aug 31, 2016 at 0:58
\$\begingroup\$ @ConorO'Brien Probably, I'm out of ideas now :( \$\endgroup\$

Adnan
– Adnan

2016-08-31 01:00:09 +00:00
Commented Aug 31, 2016 at 1:00
\$\begingroup\$ Before looking at this challenge, I got b<*>2 using a(n-1)*(a(n-1)+1)-1 \$\endgroup\$

Zwei
– Zwei

2016-09-23 03:12:36 +00:00
Commented Sep 23, 2016 at 3:12
\$\begingroup\$ @Zwei Very neat! You can actually leave out the b since that will be automatically filled in (rather than the input) :). \$\endgroup\$

Adnan
– Adnan

2016-09-23 05:48:38 +00:00
Commented Sep 23, 2016 at 5:48
1

\$\begingroup\$ Yup, I noticed that after posting. I'm surprised how well this language works for this, even though it is designed for sequences. \$\endgroup\$

Zwei
– Zwei

2016-09-23 20:29:14 +00:00
Commented Sep 23, 2016 at 20:29

Add a comment |

Community · Accepted Answer · 2017-04-13 12:39:13Z

Brain-Flak, 158 154 bytes

Leaky Nun has me beat here

({}<(()())>){({}[()]<<>(())<>([]){{}<>({}<<>(({}<>))><>)<>({<({}[()])><>({})<>}{})<>{}([])}{}<>({}())([]){{}({}<>)<>([])}{}<>>)}{}([][()]){{}{}([][()])}{}

Try it Online!

Explanation

Put a two under the input a(0)

({}<(()())>)

While the input is greater than zero subtract one from the input and...

{ ({}[()]

Silently...

Put one on the other stack to act as a catalyst for multiplication <>(())<>

While the stack is non-empty

 ([]) { {}

Move the top of the list over and copy

 <>({}<<>(({}<>))><>)

Multiply the catalyst by the copy

 <>({<({}[()])><>({})<>}{})<>{} ([]) } {}

Add one

 <>({}())

Move the sequence back to the proper stack

 ([]) { {} ({}<>)<> ([]) } {} <> >) }{}

Remove all but the bottom item (i.e. the last number created)

([][()]) { {} {} ([][()]) } {}

Dennis · Accepted Answer · 2016-08-26 03:38:36Z

5

C, 32 bytes

f(n){return--n?f(n)*~-f(n)+1:2;}

Uses 1-based indexing. Test it on Ideone.

answered Aug 26, 2016 at 3:38

Dennis

212k41 gold badges380 silver badges830 bronze badges

Add a comment |

Leaky Nun · Accepted Answer · 2016-08-26 04:10:28Z

Actually, 9 bytes

2@`rΣτu`n

Try it online!

Uses this relationship instead:

formula

which is derived from this relationship modified from that provided in the sequence:

a(n+1) = a(n) * (a(n) - 1) + 1.

Mamie · Accepted Answer · 2016-08-26 20:47:32Z

5

R, 44 42 41 bytes

2 bytes save thanks to JDL

1 byte save thanks to user5957401

f=function(n)ifelse(n,(a=f(n-1))^2-a+1,2)

edited Aug 26, 2016 at 20:47

answered Aug 26, 2016 at 8:34

Mamie

1815 bronze badges

1

\$\begingroup\$ It's not clear from the problem statement, but as long as n is guaranteed to not be negative then the condition can be reduced from n>0 to just n. \$\endgroup\$

JDL
– JDL

2016-08-26 14:26:45 +00:00
Commented Aug 26, 2016 at 14:26
\$\begingroup\$ @JDL Nice ! Thanks ! \$\endgroup\$

Mamie
– Mamie

2016-08-26 15:21:09 +00:00
Commented Aug 26, 2016 at 15:21
\$\begingroup\$ f(n-1) is 6 bytes. I think you save a byte by assigning it to something. i.e. ifelse(n,(a=f(n-1))^2-a+1,2) \$\endgroup\$

user5957401
– user5957401

2016-08-26 16:58:00 +00:00
Commented Aug 26, 2016 at 16:58

Add a comment |

Leaky Nun · Accepted Answer · 2016-08-26 02:33:18Z

Python, 38 36 bytes

2 bytes thanks to Dennis.

f=lambda n:0**n*2or~-f(n-1)*f(n-1)+1

Ideone it!

Uses this relationship modified from that provided in the sequence instead:

a(n+1) = a(n) * (a(n) - 1) + 1

Explanation

0**n*2 returns 2 when n=0 and 0 otherwise, because 0**0 is defined to be 1 in Python.

J. Sallé · Accepted Answer · 2018-08-27 16:46:36Z

K (oK), 12 bytes

{2|1+*/o'!x}

Try it online!

~~Blatantly stolen from~~ Port of Adám's answer.

Prints up to the first 11 elements of the sequence, after which the numbers become too big to handle.

Thanks @ngn for 6 bytes!

How:

{2|1+*/o'!x} # Main function, argument x. o'!x # recursively do (o) for each (') of [0..x-1] (!x) 1+*/ # 1 + the product of the list 2| # then return the maximum between that product and 2.

Leaky Nun · Accepted Answer · 2016-08-26 01:54:11Z

Jelly, 7 bytes

²_’ 2Ç¡

Try it online!

Uses this relationship provided in the sequence instead: a(n+1) = a(n)^2 - a(n) + 1

Explanation

2Ç¡ Main chain, argument in input 2 Start with 2 ¡ Repeat as many times as the input: Ç the helper link. ²_’ Helper link, argument: z ² z² ’ z - 1 _ subtraction, yielding z² - (z-1) = z² - z + 1

Leaky Nun · Accepted Answer · 2016-08-26 02:59:16Z

3

Cheddar, 26 bytes

n g->n?g(n-=1)**2-g(n)+1:2

Try it online!

Pretty idiomatic.

Explanation

n g -> // Input n, g is this function n ? // if n is > 1 g(n-=1)**2-g(n)+1 // Do equation specified in OEIS : 2 // if n == 0 return 2

edited Aug 26, 2016 at 2:59

Leaky Nun

50.6k6 gold badges115 silver badges291 bronze badges

answered Aug 26, 2016 at 1:55

Downgoat

29.2k6 gold badges85 silver badges157 bronze badges

\$\begingroup\$ Now 4 times (almost) \$\endgroup\$

Leaky Nun
– Leaky Nun

2016-08-26 01:55:51 +00:00
Commented Aug 26, 2016 at 1:55
\$\begingroup\$ Why did you remove the TIO link? \$\endgroup\$

Leaky Nun
– Leaky Nun

2016-08-26 02:35:01 +00:00
Commented Aug 26, 2016 at 2:35
\$\begingroup\$ @LeakyNun oh you must of been editing while I was \$\endgroup\$

Downgoat
– Downgoat

2016-08-26 02:51:06 +00:00
Commented Aug 26, 2016 at 2:51

Add a comment |

Dennis · Accepted Answer · 2016-08-26 03:00:56Z

3

CJam, 10 bytes

2{_(*)}ri*

Uses 0-based indexing. Try it online!

answered Aug 26, 2016 at 3:00

Dennis

212k41 gold badges380 silver badges830 bronze badges

Add a comment |

Emigna · Accepted Answer · 2016-08-26 06:37:57Z

05AB1E, 7 bytes

2sFD<*>

Explained

Uses zero-based indexing.

2 # push 2 (initialization for n=0) sF # input nr of times do D<* # x(x-1) > # add 1

Try it online!

JDL · Accepted Answer · 2016-08-26 08:25:59Z

R, 50 46 44 bytes

 n=scan();v=2;if(n)for(i in 1:n){v=v^2-v+1};v

Rather than tracking the whole sequence, we just keep track of the product, which follows the given quadratic update rule as long as ~~n>1~~ n>0. (This sequence uses the "start at ~~one~~ zero" convention)

Using the start at zero convention saves a couple of bytes since we can use if(n) rather than if(n>1)

Martin Ender · Accepted Answer · 2016-08-26 12:13:07Z

Jellyfish, 13 bytes

p \Ai &(* ><2

Try it online!

Explanation

Let's start from the bottom up:

(* <

This is a hook, which defines a function f(x) = (x-1)*x.

&(* ><

This composes the previous hook with the increment function so it gives us a function g(x) = (x-1)*x+1.

\Ai &(* ><

Finally, this generates a function h which is an iteration of the previous function g, as many times as given by the integer input.

\Ai &(* ><2

And finally, we apply this iteration to the initial value 2. The p at the top just prints the result.

Alternative (also 13 bytes)

p > \Ai (* >1

This defers the increment until the very end.

alephalpha · Accepted Answer · 2016-08-26 14:38:43Z

3

Mathematica, 19 bytes

Nest[#^2-#+1&,2,#]&

Or 21 bytes:

Array[#0,#,0,1+1##&]&

edited Aug 26, 2016 at 14:38

answered Aug 26, 2016 at 6:59

alephalpha

51.9k7 gold badges75 silver badges196 bronze badges

\$\begingroup\$ The Array solution is magical. Too bad, ##0 is not a thing. ;) \$\endgroup\$

Martin Ender
– Martin Ender

2016-08-26 15:34:44 +00:00
Commented Aug 26, 2016 at 15:34

Add a comment |

Leaky Nun · Accepted Answer · 2016-08-26 14:46:41Z

3

Prolog, 49 bytes

a(0,2). a(N,R):-N>0,M is N-1,a(M,T),R is T*T-T+1.

answered Aug 26, 2016 at 14:46

Leaky Nun

50.6k6 gold badges115 silver badges291 bronze badges

Add a comment |

Community · Accepted Answer · 2020-06-17 09:04:33Z

3

SILOS 201 bytes

readIO def : lbl set 128 2 set 129 3 j = i if j z print 2 GOTO e :z j - 1 if j Z print 3 GOTO e :Z i - 1 :a a = 127 b = 1 c = 1 :b b * c a + 1 c = get a if c b b + 1 set a b i - 1 if i a printInt b :e

Feel free to try it online!

edited Jun 17, 2020 at 9:04

CommunityBot

1

answered Aug 26, 2016 at 18:21

Rohan Jhunjhunwala

2,71619 silver badges41 bronze badges

2

\$\begingroup\$ What the hell is going on \$\endgroup\$

TuxCrafting
– TuxCrafting

2016-08-26 18:22:17 +00:00
Commented Aug 26, 2016 at 18:22
1

\$\begingroup\$ @TùxCräftîñg witchcraft \$\endgroup\$

Rohan Jhunjhunwala
– Rohan Jhunjhunwala

2016-08-26 18:22:35 +00:00
Commented Aug 26, 2016 at 18:22

Add a comment |

Wheat Wizard · Accepted Answer · 2017-06-19 15:59:22Z

Haskell, 27 bytes

f 0=2 f n=f(n-1)^2-f(n-1)+1

Try it online!

Not the shortest Haskell answer but it uses a new method.

chunes · Accepted Answer · 2021-06-05 18:03:19Z

3

Red, ^{55 49 45} 39 bytes

func[n][x: 2 loop n[x: x * x - x + 1]x]

Try it online!

-6 thanks to Galen Ivanov
-4 thanks to Pedro Maimere
-6 thanks to 9214

This is the first real thing I wrote in Red. You have been warned.

edited Jun 5, 2021 at 18:03

answered Jun 5, 2021 at 5:56

chunes

27.8k3 gold badges32 silver badges55 bronze badges

\$\begingroup\$ You can use if instead of either and explicitly return x for 49 bytes \$\endgroup\$

Galen Ivanov
– Galen Ivanov

2021-06-05 08:59:24 +00:00
Commented Jun 5, 2021 at 8:59
1

\$\begingroup\$ @GalenIvanov Thanks! \$\endgroup\$

chunes
– chunes

2021-06-05 13:37:30 +00:00
Commented Jun 5, 2021 at 13:37
\$\begingroup\$ n > 0 to n 45 bytes \$\endgroup\$

Pedro Maimere
– Pedro Maimere

2021-06-05 16:21:03 +00:00
Commented Jun 5, 2021 at 16:21
1

\$\begingroup\$ @PedroMaimere Thanks, I'll have to remember that works! \$\endgroup\$

chunes
– chunes

2021-06-05 16:30:03 +00:00
Commented Jun 5, 2021 at 16:30
1

\$\begingroup\$ What do you need if for? It will always evaluate its body if n is an integer, which is treated as truthy value. \$\endgroup\$

9214
– 9214

2021-06-05 17:38:14 +00:00
Commented Jun 5, 2021 at 17:38

| Show 3 more comments

Leaky Nun · Accepted Answer · 2016-08-26 02:20:32Z

2

C, 46 bytes

s(n,p,r){for(p=r=2;n-->0;p*=r)r=p+1;return r;}

Ideone it!

Uses p as the temporary storage of the product.

Basically, I defined two sequences p(n) and r(n), where r(n)=p(n-1)+1 and p(n)=p(n-1)*r(n).

r(n) is the required sequence.

answered Aug 26, 2016 at 2:20

Leaky Nun

50.6k6 gold badges115 silver badges291 bronze badges

1

\$\begingroup\$ Any reason you're not using the same relation from your Python answer here? That should be a lot shorter... \$\endgroup\$

Dennis
– Dennis

2016-08-26 03:20:47 +00:00
Commented Aug 26, 2016 at 3:20
\$\begingroup\$ @Dennis This is more interesting. \$\endgroup\$

Leaky Nun
– Leaky Nun

2016-08-26 03:21:08 +00:00
Commented Aug 26, 2016 at 3:21
\$\begingroup\$ @Dennis And this answer can be ported \$\endgroup\$

Leaky Nun
– Leaky Nun

2016-08-26 18:29:39 +00:00
Commented Aug 26, 2016 at 18:29

Add a comment |

Stefano Sanfilippo · Accepted Answer · 2016-08-26 12:24:54Z

C, 43, 34, 33 bytes

1-indexed:

F(n){return--n?n=F(n),n*n-n+1:2;}

Test main:

int main() { printf("%d\n", F(1)); printf("%d\n", F(2)); printf("%d\n", F(3)); printf("%d\n", F(4)); printf("%d\n", F(5)); }

Leaky Nun · Accepted Answer · 2016-08-26 12:40:53Z

Brachylog, 13 bytes

0,2|-:0&-y+*+

Try it online!

Uses this relationship instead:

formula

which is derived from this relationship modified from that provided in the sequence:

a(n+1) = a(n) * (a(n) - 1) + 1.

Sylvester's sequence

Task

Test Cases

82 Answers 82

Brain-Flak, 76 68 58 52 46 bytes

Explanation

Alternative 46-byte version

Jelly, 5 bytes

How it works

Hexagony, 27 bytes

Explanation

J, 18 14 12 bytes

J, 14 bytes

J, 18 bytes

Examples

Explanation

Perl 6, 24 bytes

Explanation

Usage:

Haskell, 26 bytes

Java 7, 46 42 bytes

Haskell, 25 bytes

S.I.L.O.S, 60 bytes

Oasis, 4 bytes

Brain-Flak, 158 154 bytes

Explanation

C, 32 bytes

Actually, 9 bytes

R, 44 42 41 bytes

Python, 38 36 bytes

Explanation

K (oK), 12 bytes

How:

Jelly, 7 bytes

Explanation

Cheddar, 26 bytes

Explanation

CJam, 10 bytes

05AB1E, 7 bytes

R, 50 46 44 bytes

Jellyfish, 13 bytes

Explanation

Alternative (also 13 bytes)

Mathematica, 19 bytes

Prolog, 49 bytes

SILOS 201 bytes

Haskell, 27 bytes

Red, 55 49 45 39 bytes

C, 46 bytes

C, 43, 34, 33 bytes

Brachylog, 13 bytes

Linked

Related

Hot Network Questions

Red, ^{55 49 45} 39 bytes