0
\$\begingroup\$

I'm having troubles trying to rearrange a set of points where each point is part of the edge of a concave polygone. My set of points is not sorted in any order, they are just randomly put in an array. See the example right below : 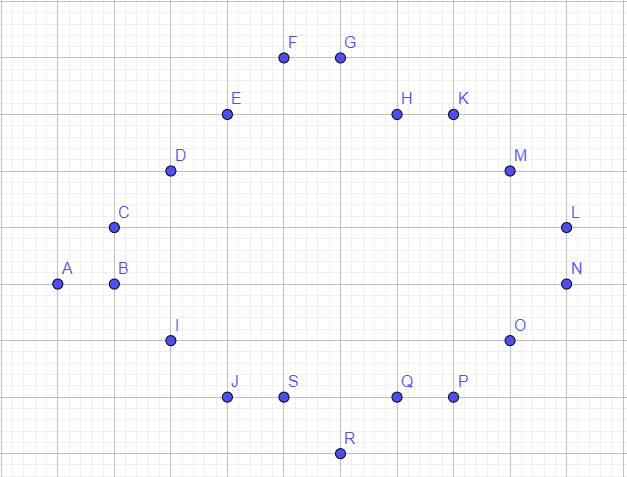enter image description here

My goal is to rearrange these points to be able to build a polygon correctly where the next index in the array is the next point to draw : 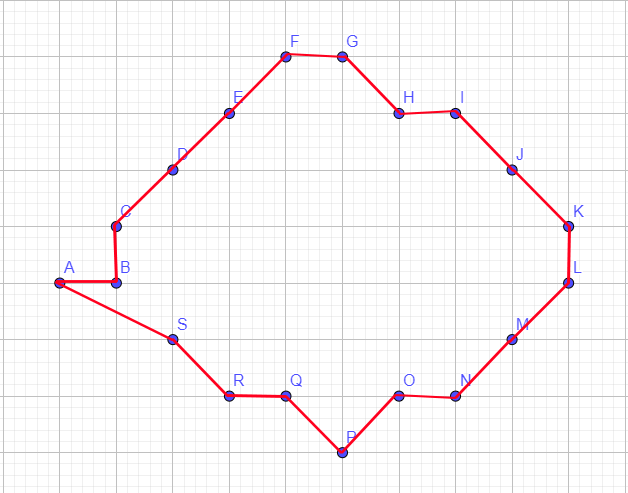enter image description here

I don't know how to do it fast, sometime arrays are made of 200 points, and I have like 20 of these arrays (I would use this to draw islands)

Thank you in advance.

\$\endgroup\$
2
  • \$\begingroup\$ I don't think this is a well defined problem. E.g. in your example, going from I to B to A to C is an equally valid convex polygon as going I , A, B, C. \$\endgroup\$ Commented Jan 10, 2019 at 1:25
  • \$\begingroup\$ Yes but it's not a problem as I want to find one of the concave polygone that may be build out of a set of points. \$\endgroup\$ Commented Jan 10, 2019 at 9:13

1 Answer 1

Reset to default
1
\$\begingroup\$

Maybe sort them on angle of vector from average to point?

In pseudo code:

MID = AVERAGE(PTS) ANGLES = [] FOR EACH PT: V = PT - MID ANG = ATAN2F( PT.Y, PT.X ) ANGLES.APPEND( (ANG, PT ) ) SORT( ANGLES ) FOR ANG,PT IN ANGLES: OUTPUT(PT)
\$\endgroup\$
2
  • \$\begingroup\$ Thank you for your answer but I think this méthod does not work with concave polygon as I already tried it and it builds a convex polygon out of these points. In the example I provided it's not that easy to see. \$\endgroup\$ Commented Jan 10, 2019 at 9:10
  • \$\begingroup\$ This looks workable to me if we can reliably place the center point in the polygon's interior, though I think we need some additional sorting by distance when we encounter a run of 3 or more points along a ray from our centroid (all at the same angle, to within some tolerance). If the average point lies outside the expected polygon (think of a very skinny crescent moon with narrow tips that almost wrap around) we'll get a less desirable result. This method implicitly assumes the polygon is "star-shaped" in the mathematical sense, which covers non-convex cases but not every concave polygon. \$\endgroup\$ Commented Jan 10, 2019 at 12:37

You must log in to answer this question.

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.