0
$\begingroup$

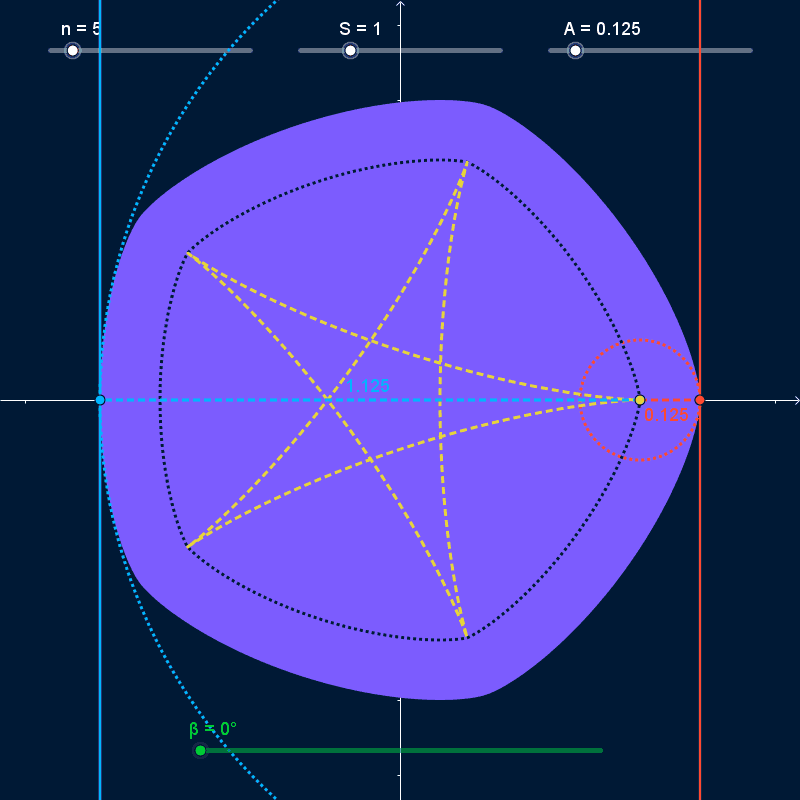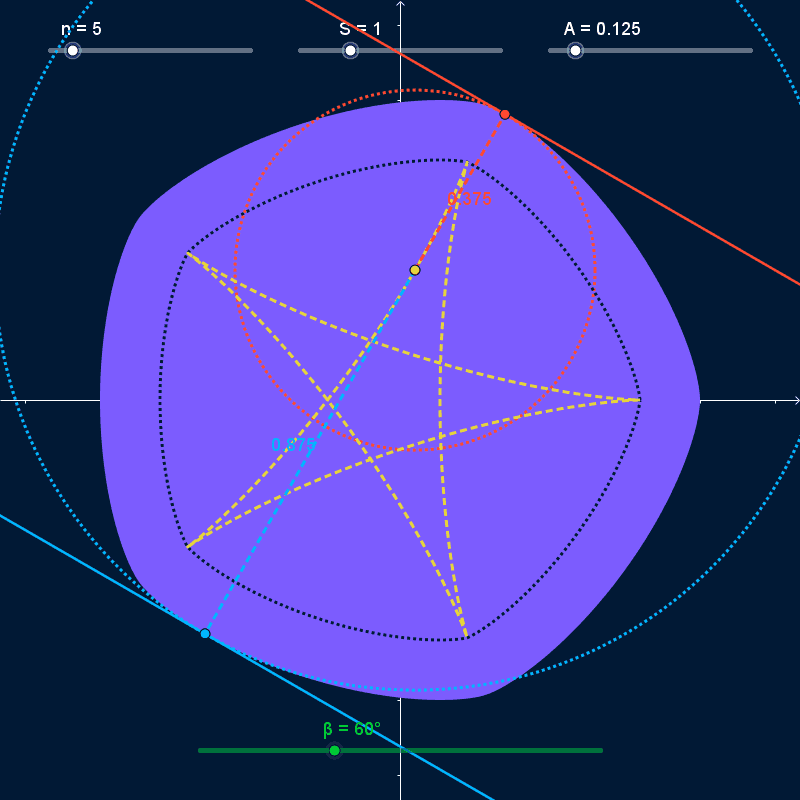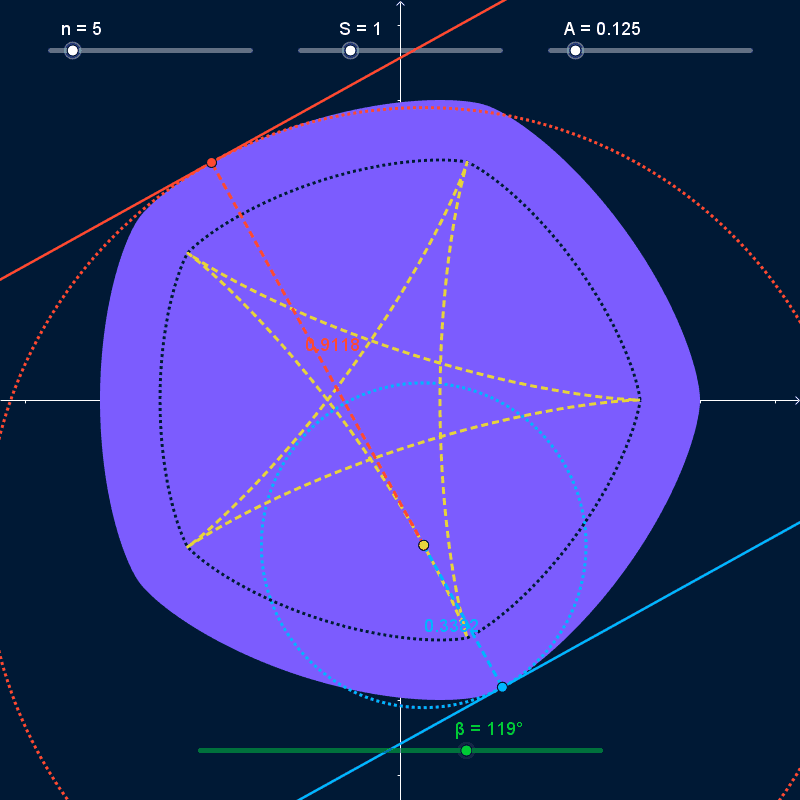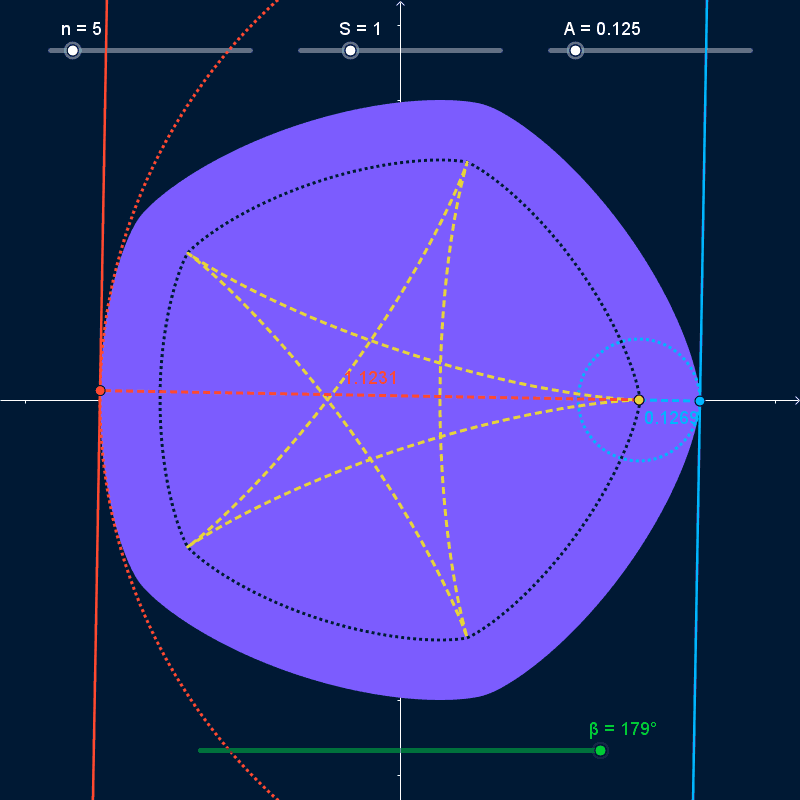
Given the functions $$ p(θ) = \frac{S}{2} × \frac{\cos\bigl(n × (θ - α)\bigr)}{n^2 - 1} + \frac{W}{2}\\ \begin{align} X(θ) = \cos(θ) × &p(θ) - \sin(θ) × p'(θ) - \left(p\left(\frac{0}{2}\right) - \frac{W}{2}\right)\\ Y(θ) = \sin(θ) × &p(θ) + \cos(θ) × p'(θ) - \left(p\left(\frac{π}{2}\right) - \frac{W}{2}\right) \end{align} $$ the curve $\bigl(X(t), Y(t)\bigr), 0° ≤ t < 360°$ is a smooth, regular $n$-sided polygonal Curve of Constant Width (CoCW) where

  • $p'(θ)$ is the derivative of $p(θ)$ with respect to $θ$,
  • $A > 0$ is the radius of the smallest osculating circle on the curve,
  • $S + A > 0$ is the radius of the largest osculating circle on the curve,
  • $W = S + 2 A$ is the total width of the curve, and
  • $α$ is an angle parameter that rotates the curve about the origin.
  • (If $A = 0$, the curve has sharp corners at the "vertices" and thus loses the property of being everywhere-smooth, but everything else holds. If $S = 0$, the curve becomes a circle with radius $A$.)

We also define $N := n - \sin\left(\frac{π}{2} × n\right)$.

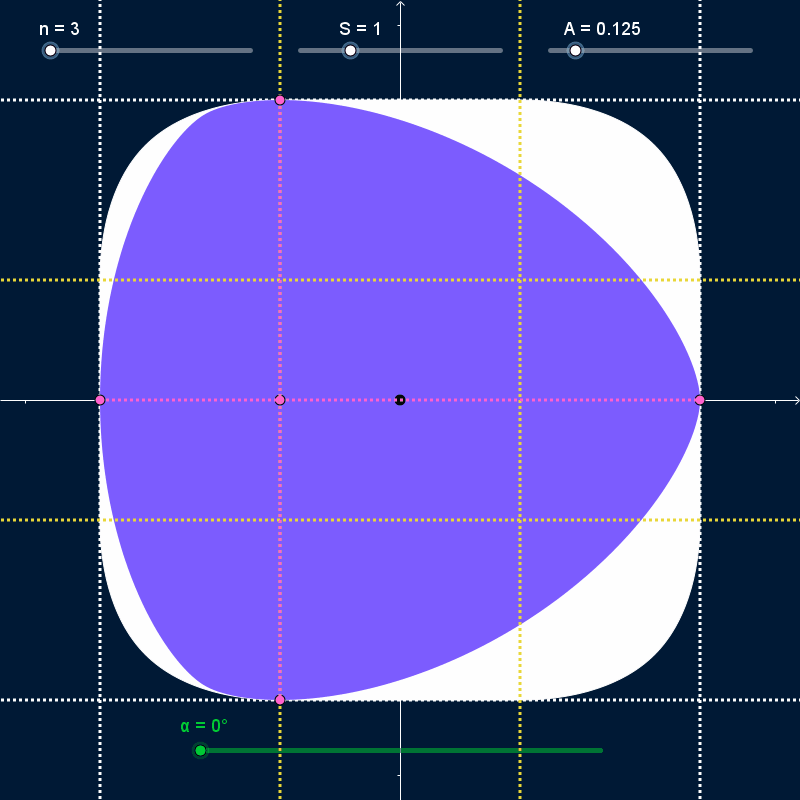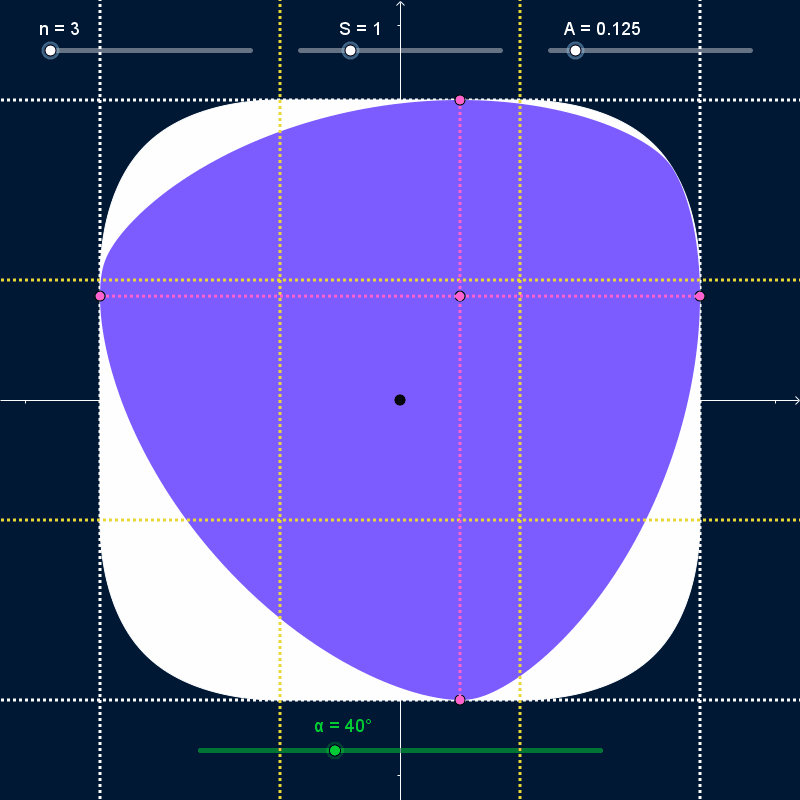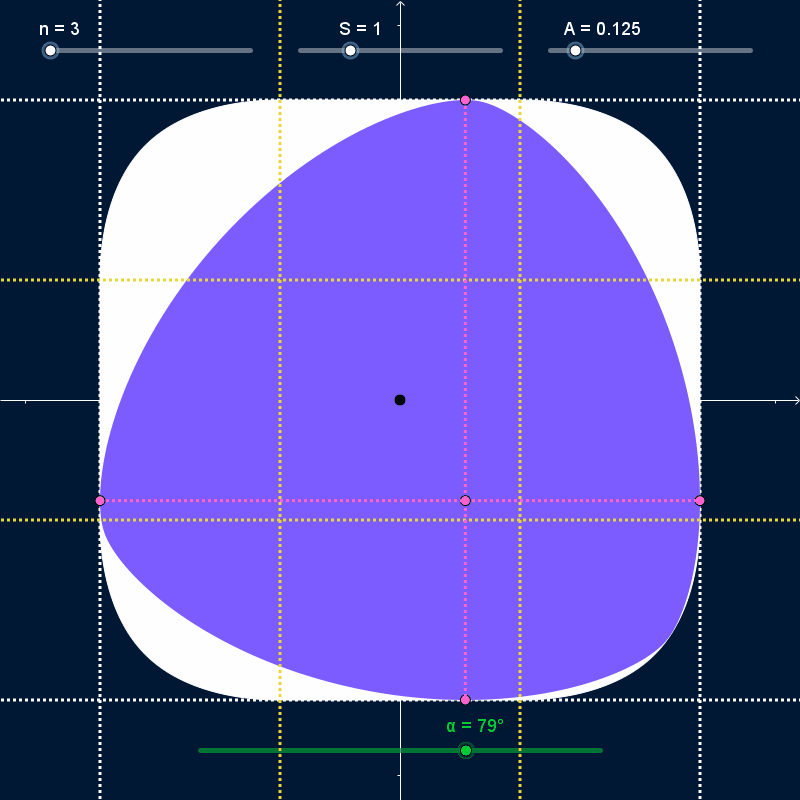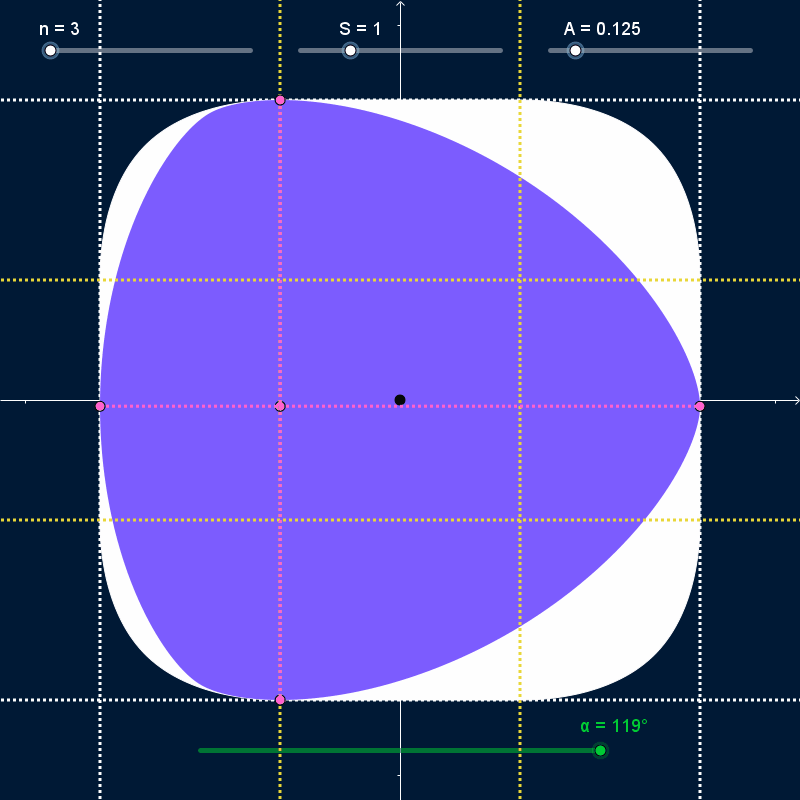
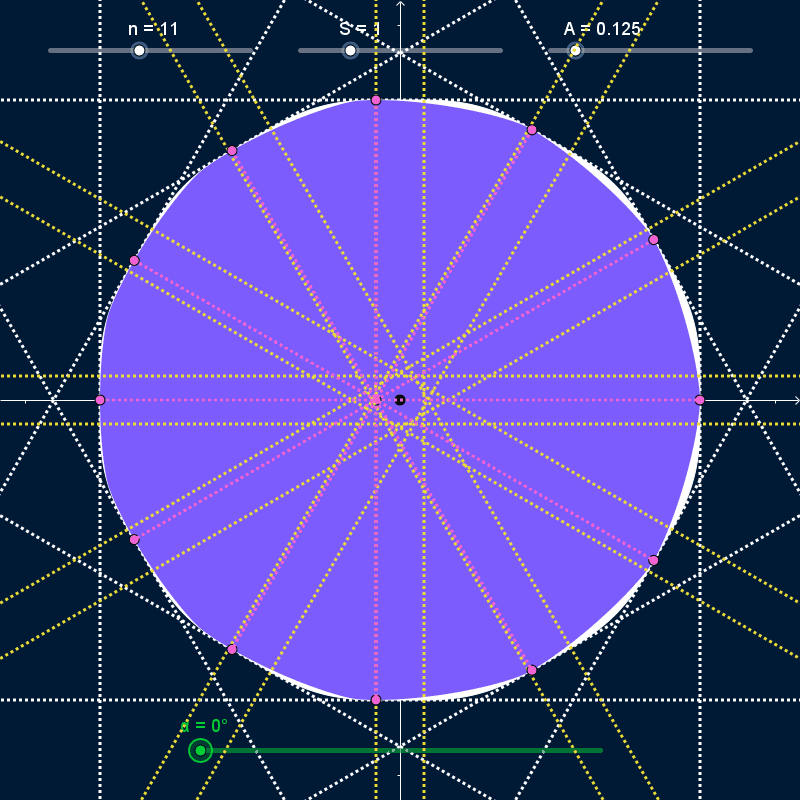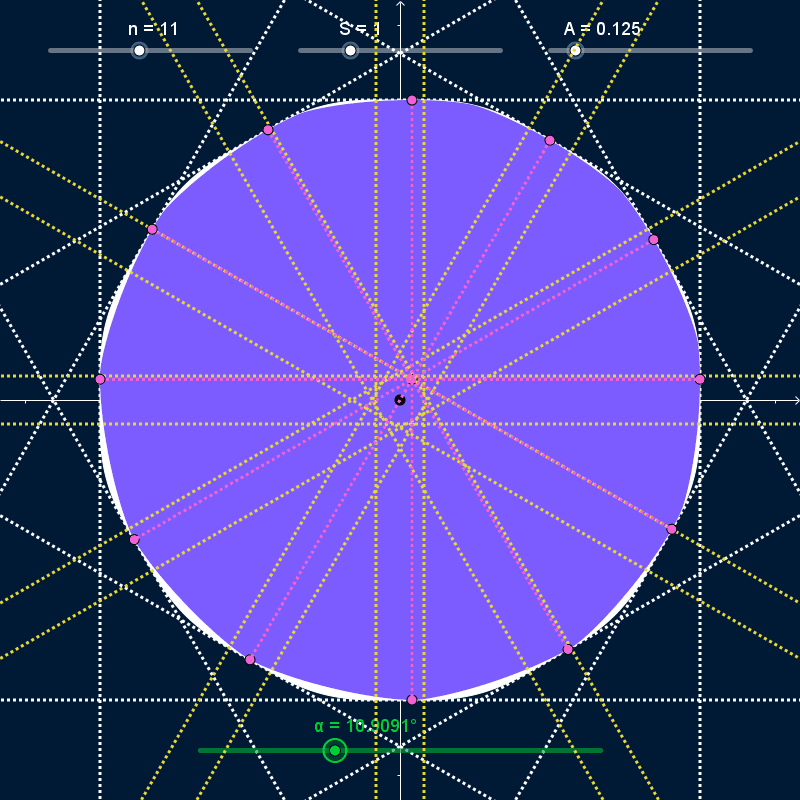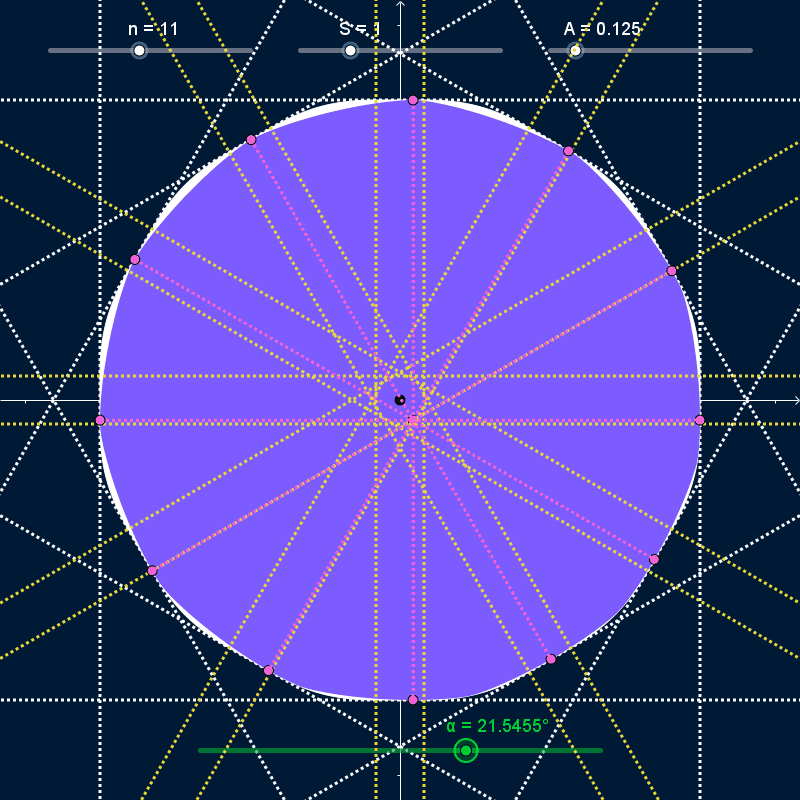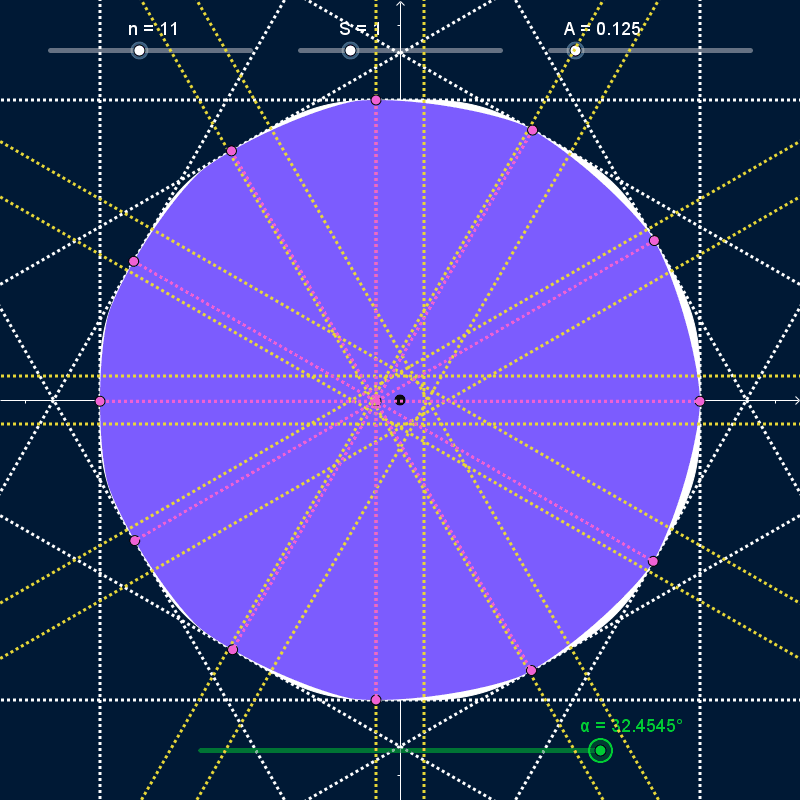
As $α$ varies and the curve rotates, it stays bounded inside a regular polygon with $N$ sides centered on the origin with width and height equal to $S + 2 A$ (dashed white lines in the GIFs below). At all times, the curve touches every side of the bounding polygon at exactly one point (pink points in the GIFs below). However, the rotating curve doesn't completely cover the bounding polygon; the covered area (solid white in the GIFs below) has rounded corners. I want to find the precise shape of those corners.

Three-sided curve rotating inside a square.

Seven-sided curve rotating inside an octagon.

Eleven-sided curve rotating inside a dodecagon.

The bounding-box isn't completely rounded. It has a straight line-segment as the center of all four sides, with length $\frac{S × N}{n^2 - 1}$ (bounded by yellow lines in the GIFs above). However, I'm not sure how to find mathematical descriptions of the curves that join those straight segments together.

A Note on Osculating Circles for Cye Waldman

Given a point on a curve, an osculating circle shares a tangent with the curve at that point and has curvature (inverse of radius) equal to the curvature of the curve at that point. With the CoCW in this question being defined by the functions $X(t)$, $Y(t)$, we can draw two points on the curve $P_{1} = \bigl(X(β), Y(β)\bigr)$ and $P_{2} = \bigl(X(β + π), Y(β + π)\bigr)$. Because we are dealing with a CoCW, the tangents of the curve at these two points are parallel for any $β$ and the center-points of the osculating circles at both points are the same, located at $P_{0} = \bigl(X(β) - Y'(β), Y(β) + X'(β)\bigr)$. As we let $β$ vary, the smallest radius of the osculating circles on this curve will be $A$, and the largest radius will be $S + A$.

Animation of osculating circles of a five-sided curve.

$\endgroup$
17
  • $\begingroup$ Is $p'(\theta)$ the derivative of $p(\theta)$? If not, then what does $p'$ mean? And if so, then what in the H*** are you doing mixing angles measured in degrees with derivatives? Are you insane?? $\endgroup$ Commented Mar 22, 2024 at 19:47
  • $\begingroup$ I'm sorry, but I've plotted this for $n=5, S=10, A=5, \alpha=0$ and I don't see anything but a pudgy pentagon. I had the impression that was to see something like an annulus, Can you please add a sample calculation and figure. $\endgroup$ Commented Mar 22, 2024 at 23:08
  • $\begingroup$ @CyeWaldman I added a GIF of the curve (white) rotating inside its bounding box (purple). Note that $α$ is not static. $\endgroup$ Commented Mar 23, 2024 at 1:47
  • $\begingroup$ Very nice, that will help anyone who is looking at this question. $\endgroup$ Commented Mar 23, 2024 at 14:28
  • $\begingroup$ @PaulSinclair $p'(θ)$ is the derivative of $p(θ)$, yes. And the degrees work perfectly well. $\endgroup$ Commented Mar 23, 2024 at 14:46

2 Answers 2

Reset to default
1
$\begingroup$

I figured out that the point $\bigl(X(θ), Y(θ)\bigr)$ at $θ = \frac{n × α - \frac{π}{2}}{D}$, where $D := \frac{n + \sin\left(\frac{π}{2} × n\right)}{2}$, traces out a corner of the envelope-polygon as $α$ varies. Re-writing the equations for the CoCW in terms of $α$ with that substitution, we get $$ p_{env}(α) = \frac{S}{2} × \frac{\cos\left(n × \left(\frac{n × α - \frac{π}{2}}{D} - α\right)\right)}{n^2 - 1} + \frac{W}{2}\\ p_{env}'(α) = -\frac{S}{2} × \frac{\sin\left(n × \left(\frac{n × α - \frac{π}{2}}{D} - α\right)\right)}{n^2 - 1} × n\\ \begin{align} X_{env}(α) = \cos\left(\frac{n × α - \frac{π}{2}}{D}\right) × &p_{env}(α) - \sin\left(\frac{n × α - \frac{π}{2}}{D}\right) × p_{env}'(α) - \frac{S}{2} × \frac{\cos\left(n × \left(\frac{0}{2} - α\right)\right)}{n^2 - 1}\\ Y_{env}(α) = \sin\left(\frac{n × α - \frac{π}{2}}{D}\right) × &p_{env}(α) + \cos\left(\frac{n × α - \frac{π}{2}}{D}\right) × p_{env}'(α) - \frac{S}{2} × \frac{\cos\left(n × \left(\frac{π}{2} - α\right)\right)}{n^2 - 1} \end{align} $$

Plotted $\bigl(X_{env}(t), Y_{env}(t)\bigr)$ for $0° ≤ t < 360° × \frac{D}{n}$ gives the entire curve, which touches every-other corner of the envelope-polygon (reflecting it about the vertical axis covers all the corners that the first curve misses). Trimming it down to $\frac{90°}{n} ≤ t < \frac{360°}{N} - \frac{90°}{n}$, remembering that $N := n - \sin\left(\frac{π}{2} × n\right)$, gives a single corner. Rotating that corner about the origin $N - 1$ times by an angle of $\frac{360°}{N}$ gives the remaining corners.

Curves for n = 3

Curves for n = 7

Curves for n = 11

$\endgroup$
0
$\begingroup$

I have looked at this problem, reformulated it a bit, and developed a credible solution to envelope of curves described in the original post (OP). I work in the complex plane, so have reformatted the equations as follows,

$$ p(\theta)=\frac{S}{2}\frac{\cos (n(\theta-\alpha))}{n^2-1}\\ z(\theta)=\bigg(p(\theta)+ \frac{S}{2}+A \bigg)e^{i\theta}+i p’(\theta) e^{i\theta} $$

You’ll notice that I’ve dropped the translation terms $p(1)+ip(\pi/2)$ as they become superfluous when the solutions for various $\alpha$ are aligned in a single square box and the origin is moved to the center. Here, as in the OP, we have taken $S=1.25, A=S/2$.

To delineate the envelope of the solutions, i.e., the purple zone in the OP, I plotted the solution for 360 values of $\alpha$ on a single plot. This is shown in the first figure below. The red circle is shown for reference and comparison. The blue dashed lines indicate the straight sections of the envelope as called out in the OP. Our job is to find an analytic approximation to the outer envelope, The red star shows the pseudo-origin for developing the curve fit of the envelope. It is obvious that the envelope is not circular but must be close to it. Moreover, we see that it must be symmetric about the $45^{\circ}$-line.

This suggested to me to look at the superellipse. (Some readers may be familiar with the squircle, which will do just as well.) The superellipse is a special case of the superconics curves. The simple form for a curve in the first quadrant is

$$ y=(1-x^q)^{1/q},\quad x\in[0,1] $$

We note that $q=2$ is a circle, of course. And this must be scaled to the actual size of the envelope (details below). I found empirically the for $n=5$ as in the figure below, $q\approx2\cdot1.025641$. The envelope so calculated is shown in magenta in the figure.

Specifically, the pseudo-origin is given by $z_0=d(1+i)$, where, as per the OP,

$$ d=\frac{S}{2}\biggr( \frac{n-\sin(n\pi/2)}{n^2-1}\biggr) $$

The scaling factor is the distance from the origin to the side wall ($w=S/2+A$) less the distance to the pseudo-origin, thus giving the scaling factor $s=w-d$.

Similar calculations were carried out for the case $n=3$. Everything up to the empirical calculation of $q$ is identical, except for $n$, of course. Here we found that $q\approx2\cdot1.086957$. These results are shown in the second figure below.

We also looked at $n=7$ and $n=9$. Here we found that there are eight flat sections rather than four and did not go any further for the time being.

ConstWidthCurves: n=5 ConstWidthCurves: n=3

$\endgroup$
5
  • $\begingroup$ While the superellipse curve comes close to the shape of the envelope for $n = 3$ and $n = 5$, it isn't perfect. I'd like to find the exact shape, not just an approximation, and I'd like it to apply for higher values of $n$ where the envelope isn't square. $\endgroup$ Commented Mar 28, 2024 at 14:31
  • $\begingroup$ @Lawton Personally, I think that what you seek is not possible. However, as a first step, I suggest that find a numerical description of the envelope, which you need for verification of any analytical solution. I tied to characterize the envelope by tracing the outermost point of the curve, but that does not define envelope. In fact, it's almost immediately run over by the subsequent $\alpha$ solutions. In fact, it doesn't seem to be good anywhere except the flat regions. So, I'll suggest that you try to define that envelope before you seek any kind of analytical solution. And good luck. $\endgroup$ Commented Mar 28, 2024 at 16:53
  • $\begingroup$ I figured out a solution for the exact corner shape and posted it as an answer. $\endgroup$ Commented Apr 15, 2024 at 16:32
  • $\begingroup$ Congratulations, sincerely. But I see that you've changed the equations in the OP and I haven't the energy to redo all the work necessary to check this out. $\endgroup$ Commented Apr 15, 2024 at 18:48
  • $\begingroup$ The only change was moving the width-adjustment term into the support function $p$ to fit with what seems to be standard practice based on my continued research into this topic. That makes the complex-reformatting become $Z(θ) = \bigl(p(θ) + i p'(θ)\bigr) e^{i θ} - p(0) - i p\left(\frac{π}{2}\right) + \frac{W}{2} (1 + i)$. $\endgroup$ Commented Apr 16, 2024 at 13:50

You must log in to answer this question.

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.