0
$\begingroup$

I'm completely new to Mathematica and stuck on how to go about trying to fit a Gaussian function to my data. Pretty clueless and nothing I've tried has worked.

Can anyone help?

I've imported the data and plotted it, but not sure what to do next...

G' = Import["GP S3 F2 G' LX.txt", "Table"] ListLinePlot[Derivative[1][G], PlotTheme -> "Scientific", PlotRange -> {{2620, 2730}, {0, 2750}}]

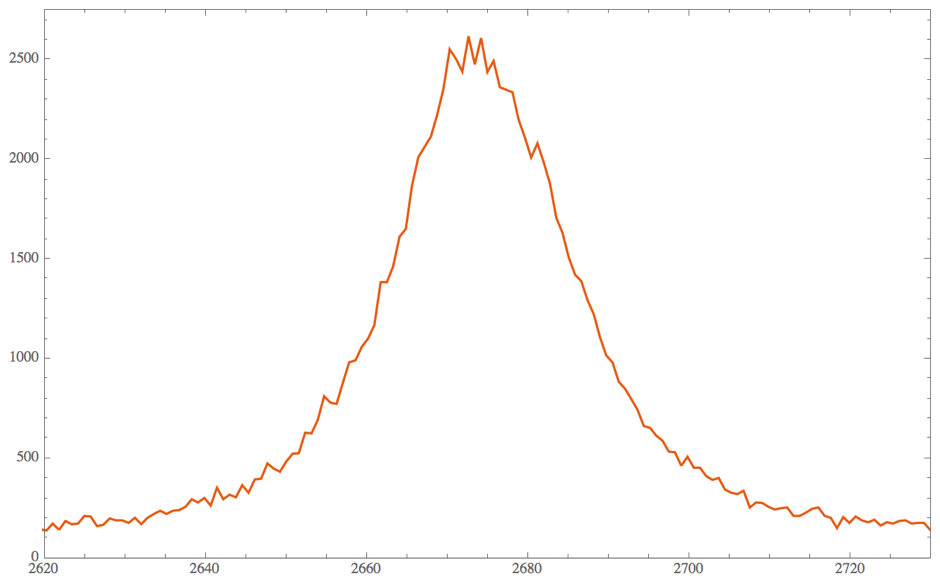
Plot of data

Improve this question
$\endgroup$
7
  • 1
    $\begingroup$ Check out FindDistributionParameters $\endgroup$ Commented Nov 27, 2017 at 20:01
  • 1
    $\begingroup$ @ChrisK. I disagree. This is a regression problem where the fitted curve has a similar shape to a Gaussian probability function (a + b Exp[(x-c)^2/d]) rather than fitting a probability distribution from a random sample. $\endgroup$ Commented Nov 27, 2017 at 20:07
  • $\begingroup$ @JimB Good point -- I should avoid weighing in on statistical questions, which are outside my area of expertise! $\endgroup$ Commented Nov 27, 2017 at 20:09
  • 3
    $\begingroup$ Try Normal@NonlinearModelFit[G', a+ b*Exp[ (x-c)^2/d], {a, b, c, d}, {x, y}]. You will get the fitting equation. A better reply could be provided if you give us access to the data G' $\endgroup$ Commented Nov 27, 2017 at 20:22
  • 2
    $\begingroup$ If you have trouble with convergence following @JoséAntonioDíazNavas good suggestion, then you should include starting values (different from the default values of 1 for all parameters). You might try {{a, 100}, {b, 2500}, {c, 2675}, {d, -400}}. $\endgroup$ Commented Nov 27, 2017 at 20:49

2 Answers 2

Reset to default
1
$\begingroup$

With NMinimize it's easy to solve the problem. Because there is no data provided I create some example data 

data = Block[{mu = 1, sig = .73},Map[{#,Exp[-(1/2) ((# - mu)/sig)^2]/(sigSqrt[2 Pi])RandomReal[{0.9, 1.1}]} &, RandomReal[{-1, 3}, 100]]]; ListPlot[data]

of a perturbed gauss. The optimal approximation follows from

res = Map[(Exp[-(1/2) ((#[[1]] - mu)/sig)^2]/(sig Sqrt[2 Pi]) - #[[2]])^2 &, data]; J = res.res; NMinimize[J, {mu, sig}] {0.000044725, {mu -> 0.996546, sig -> 0.746079}}

Alternativly the solution could be obtained with 

NonlinearModelFit[data, Exp[-(1/2) ((x - mu)/sig)^2]/(sig Sqrt[2 Pi]), {mu, sig}, x] Show[{bild, Plot[Normal[%], {x, -3, 3}]}]
Improve this answer
$\endgroup$
5
  • $\begingroup$ @UlrichNeumann thanks so much! Would it help more if I provided the data? I can't work out how to attach a file here $\endgroup$ Commented Nov 28, 2017 at 12:10
  • 1
    $\begingroup$ I suggest using PDF[NormalDistribution[mu, sig], x] instead of typing out the PDF function. $\endgroup$ Commented Nov 28, 2017 at 12:29
  • $\begingroup$ @user53761 You could reduce your data if necessary and provide it as an outputcell... $\endgroup$ Commented Nov 28, 2017 at 14:15
  • $\begingroup$ @UlrichNeumann I'm sorry, I realise this is a ridiculous way to share the data $\endgroup$ Commented Nov 28, 2017 at 17:55
  • $\begingroup$ I agree ;-) ! What I meant is edit your question and append there(!) an outputcell with your data {...,{xi,yi},...}! $\endgroup$ Commented Nov 29, 2017 at 15:41
0
$\begingroup$

as other users replied, you should provide the input data.

Anyway, note that the area underlying the graph is bigger than one- you should compute this total area, call it A, and divide every y by A, so that you have area=1. Then do compute the average and the standard deviation for the new distribution, put these two numbers (mu, sigma) into the formula for the normal distribution, then multiply back by the A factor. Try plotting this against your data.

Also.. You know that gaussian distributions tend to 0 for x->+-inf. In your case, not sure if the sample is shifted up by summing factor.. Do take that into consideration. (find the shifting factor a, subtract this number to all the points (to all the y's), before computing the total area).

Of course, @ChrisK and @JimB summed this up by telling to find the a,b,c,d parameters.

Improve this answer
$\endgroup$
1
  • $\begingroup$ While this addresses part of OP's concerns, a valid answer should probably contain a code sample to show how to apply mentioned notes. At the end it is about Mathematica, not math / stats. $\endgroup$ Commented Nov 28, 2017 at 10:41

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.