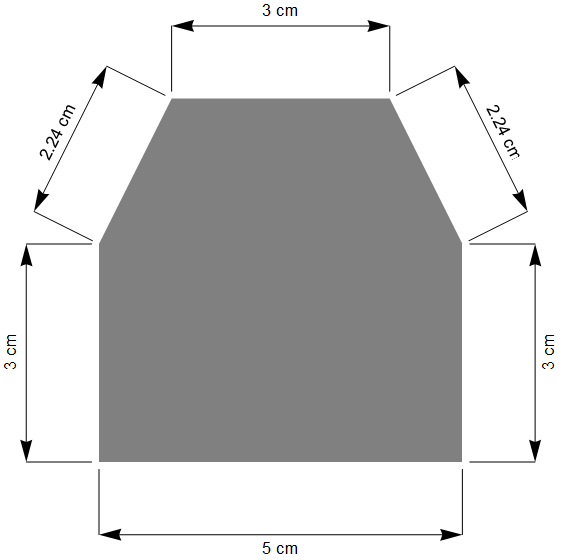
ClearAll@dim; dim[{a_, b_}, label_String, d_] := Module[{n = Normalize[RotationTransform[\[Pi]Normalize[RotationTransform[π/2][b - a]], t = Arg[(b - a).{1, I}], r}, If[t > \[Pi]π/2, t -= \[Pi]];π]; { Arrowheads[{-0.04, 0.04}], Arrow[{a + d n, b + d n}], Line[{a + 0.1 d n, a + d n}], Line[{b + 0.1 d n, b + d n}], Rotate[Text[label, (a + b)/2 + 1.2 d n, {0, 0}], t, (a + b)/2 + 1.2 d n] }]; EDIT:
This seems to have garnered a bit of attention, so I might tidy up a couple of aspects.
ClearAll@dim; dim[{a_, b_}, d_, round_:1] := Module[{ n = Normalize[RotationTransform[π/2][b - a]], t = Arg[(b - a).{1, I}], text}, text = ToString@Round[Norm[a - b], round]; If[d < 0, text = "\n" <> text, text = text <> "\n"]; {Arrowheads[{-0.04, 0.04}], Arrow[{a + d n, b + d n}], Line[{a + 0.1 d n, a + d n}], Line[{b + 0.1 d n, b + d n}], Rotate[Text[text, (a + b)/2 + d n, {0, 0}], t, (a + b)/2 + d n]}]; This version has much better positioning of the labels. The previous version had a scale factor based on the distance $d$. The further out it was, the further away from the dimension line. This version uses a newline \n to position the text consistently across any distance.
This version also automatically calculates the distance for you, instead of a user supplied label. The distance can be optionally rounded to whatever accuracy required. One could chop, change and combine label generation as required.
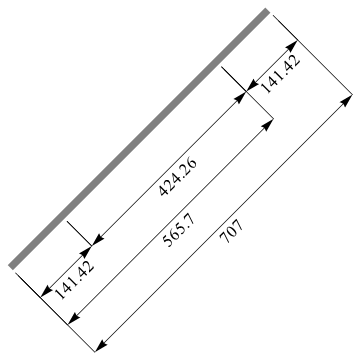
An example with labels at various distances:
Graphics[{{Gray, Polygon[{{0, 0}, {500, 500}, {490, 510}, {-10, 10}}]}, dim[{{0, 0}, {100, 100}}, -75, 0.01], dim[{{100, 100}, {400, 400}}, -75, 0.01], dim[{{400, 400}, {500, 500}}, -75, 0.01], dim[{{0, 0}, {400, 400}}, -150, 0.1], dim[{{0, 0}, {500, 500}}, -225] }]