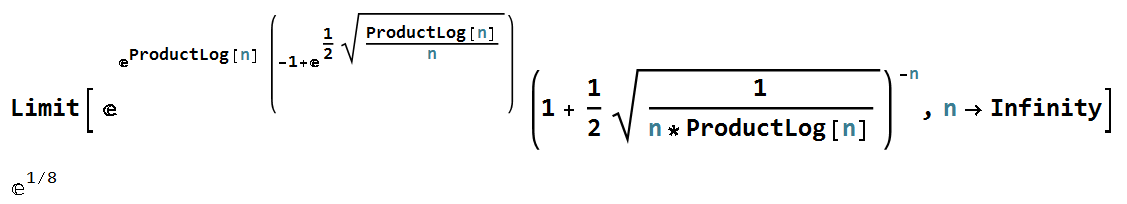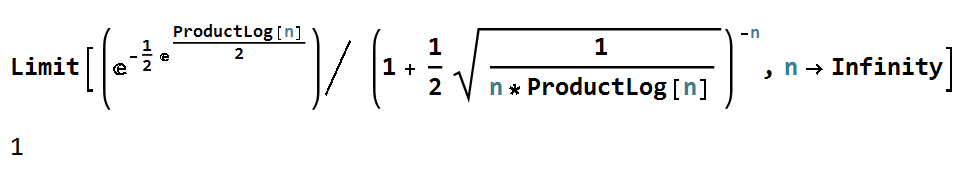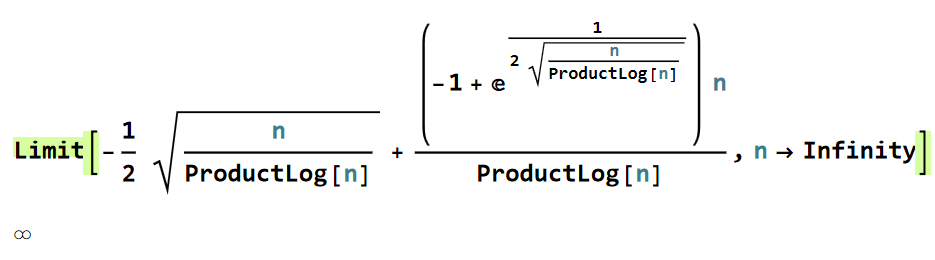6
$\begingroup$

Bug introduced in 12.0.0.0. and persisting through 14.3.

I wanted to calculate this limit:

 Limit[E^(E^ProductLog[n] (-1 + E^(1/2 Sqrt[ProductLog[n]/n]))) (1 + 1/2 Sqrt[1/(n*ProductLog[n])])^-n, n -> Infinity]

The correct result is E^(1/8)

correct limit

Furthermore, it is true that

 Limit[(E^(-(1/2) E^(ProductLog[n]/2)))/ (1 + 1/2 Sqrt[1/(n*ProductLog[n])])^-n, n -> Infinity]

is equal to 1 true limit

Therefore, it must be

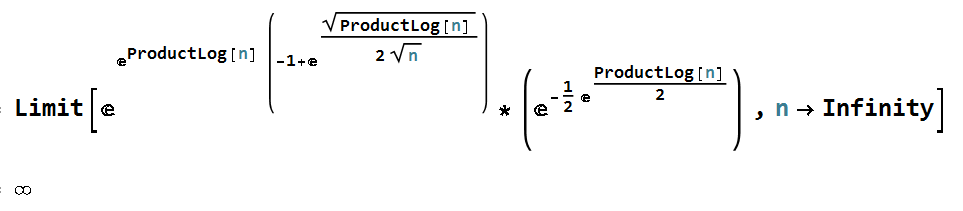
 Limit[E^(E^ProductLog[n] (-1 + E^(Sqrt[ProductLog[n]]/(2 Sqrt[n]))))*(E^(-(1/2) E^(ProductLog[n]/2))) , n -> Infinity]

also equal to E^(1/8) But the result shocked me. Mathematica gives Infinity !!!

wrong limit

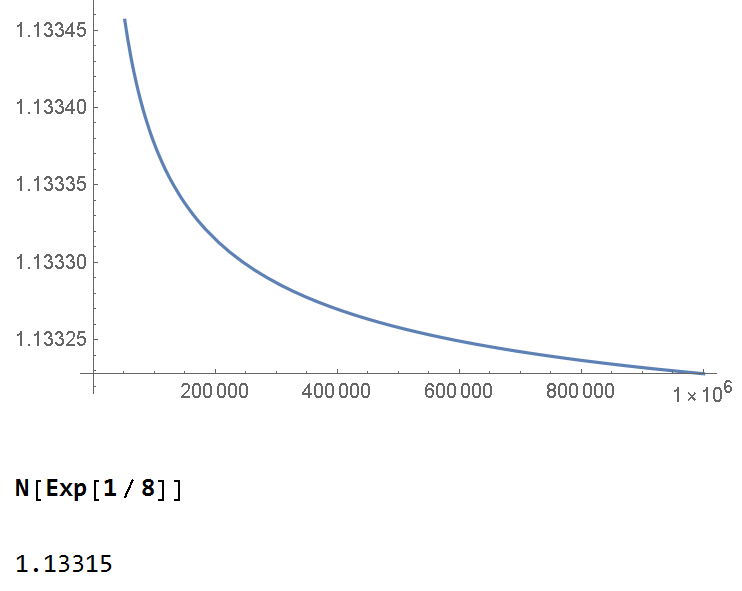
The graph confirms my original assumption

 Plot[E^(E^ProductLog[n] (-1 + E^(Sqrt[ProductLog[n]]/(2 Sqrt[n]))))*(E^(-(1/2) E^(ProductLog[n]/2))) , {n, 1, 1000000}]

graph

On deeper analysis, I was able to better isolate the problem and have the following simpler example.

 Limit[-(1/2) Sqrt[n/ProductLog[n]] + ((-1 + E^(1/(2 Sqrt[n/ProductLog[n]]))) n)/ ProductLog[n], n -> Infinity]

again gives the wrong result of Infinity

wrong limit

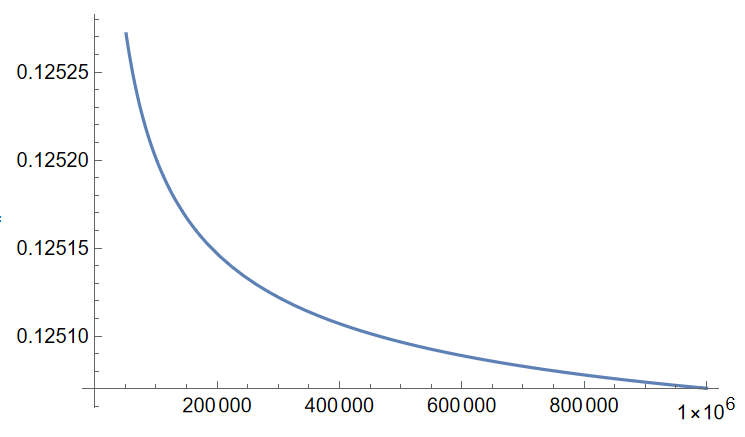
The limit is equal to 1/8, which is supported by the following graph

 Plot[-(1/2) Sqrt[n/ProductLog[n]] + ((-1 + E^(1/(2 Sqrt[n/ProductLog[n]]))) n)/ ProductLog[n], {n, 1, 1000000}]

tends to 1/8

Improve this question
$\endgroup$
13
  • 1
    $\begingroup$ Please report to Wolfram Technical Support <[email protected]>. $\endgroup$ Commented Jul 8, 2022 at 20:25
  • 1
    $\begingroup$ Question is in the title: Why do these identical limits give different results? $\endgroup$ Commented Jul 8, 2022 at 21:18
  • 1
    $\begingroup$ What do you mean, "why?" Do you want to know where the computation goes differently internally? That is, a comparison of the codes in the different versions? You should ask Wolfram about that. You seem to know the correct answer and you call it a bug in a comment. What more do you want to know? $\endgroup$ Commented Jul 8, 2022 at 21:23
  • 2
    $\begingroup$ fyi, I checked V 13.2, and it still gives $\infty$ $\endgroup$ Commented Dec 8, 2022 at 1:43
  • 1
    $\begingroup$ And still no bug report. Might or might not be a coincidence. $\endgroup$ Commented Jul 10, 2023 at 18:07

2 Answers 2

Reset to default
7
$\begingroup$

The easiest way, by a limited approach corresponding to approaching positive infinity:

expr = -(1/2) Sqrt[ n/ProductLog[n]] + ((-1 + E^(1/(2 Sqrt[n/ProductLog[n]]))) n)/ ProductLog[n]; Limit[expr /. n -> 1/n, n -> 0, Direction -> "FromAbove"] (* 1/8 *)

Another workaround:

Limit[SeriesCoefficient[expr, {n, Infinity, 0}], n -> Infinity] (* 1/8 *)

Possible cause of trouble:

The series at infinity seems divergent:

sd = Series[expr, {n, Infinity, 2}]; seriescoeffs = sd[[3]]; firstnumerator = sd[[4]]; denominator = sd[[6]]; kk = firstnumerator - 1; (++kk; a[kk] (n^(kk/denominator)) -> Limit[Simplify[# (n^(kk/denominator))], n -> Infinity]) & /@ seriescoeffs (* {a[-1]/Sqrt[n] -> 0, a[0] -> 1/8, Sqrt[n] a[1] -> \[Infinity], n a[2] -> \[Infinity], n^(3/2) a[3] -> \[Infinity], n^2 a[4] -> \[Infinity]} *)
Improve this answer
$\endgroup$
5
$\begingroup$

A partial workaround.

$Version (* "13.1.0 for Mac OS X x86 (64-bit) (June 16, 2022)" *) Clear["Global`*"] f[n_] = -(1/2) Sqrt[ n/ProductLog[n]] + ((-1 + E^(1/(2 Sqrt[n/ProductLog[n]]))) n)/ ProductLog[n] // FullSimplify (* -(1/2) Sqrt[E^ProductLog[n]] + E^ProductLog[n] (-1 + E^(1/(2 Sqrt[E^ProductLog[n]]))) *)

Using Asymptotic

asymp = Asymptotic[f[n], n -> Infinity] // Simplify[#, n > 1] &; Limit[asymp, n -> Infinity] (* 1/8 *)

Or using Series

ser = Series[f[n], {n, Infinity, 1}] // Normal // Simplify[#, n > 1] &; Limit[ser, n -> Infinity] (* 1/8 *)
Improve this answer
$\endgroup$
1
  • 1
    $\begingroup$ Interesting that this gave me infinity: Series[expr, {n, Infinity, 1}] // Normal // Simplify // Limit[#, n -> Infinity] & b/c expr wasn't simplified. $\endgroup$ Commented Jul 8, 2022 at 23:25

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.