I am looking for better, preferably analytical approaches to discretize intersections of algebraic surfaces. When surfaces are not identical, these solutions are either curves or points.
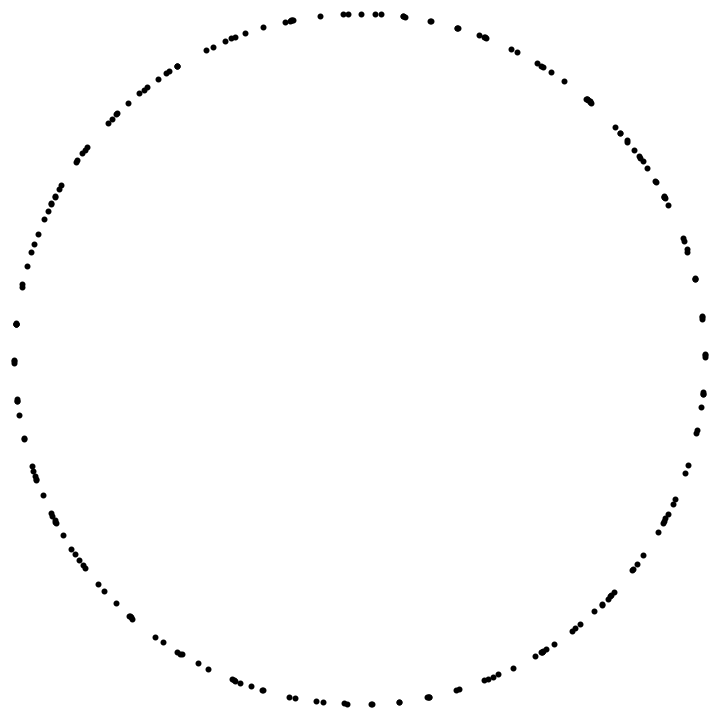
An extremely simplified example of problems with plain old DiscretizeRegion can be seen below. In this case algebraic surfaces are just spheres, and their intersection is a circle. In this example, I extract points in the discretized version for a specific pair of spheres, and rotate them to match a planar circle:
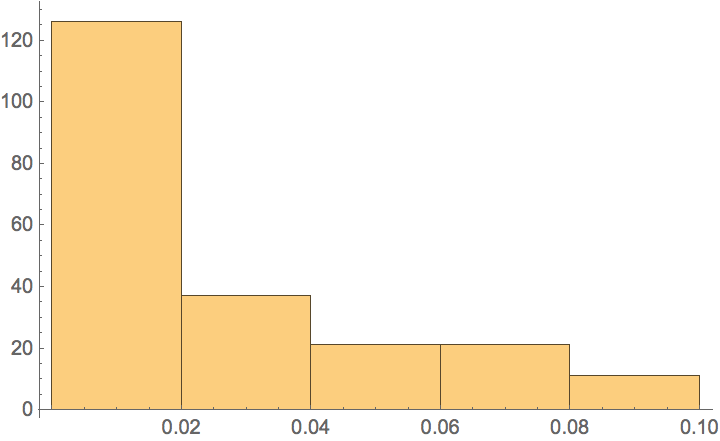
MeshPrimitives[DiscretizeRegion@RegionIntersection[Sphere /@ {-#, #}], 0] /. coord : {Repeated[_?NumericQ, {3}]} :> RotationTransform[{#, {0, 0, 1}}][coord][[1 ;; 2]] &@ {0.09666984222273534`, 0.3622850077710253`, 0.33076353297934696`} // Graphics That doesn't really look like a good distribution one would expect from just intersecting two spheres. Histogram of line lengths looks equally bad:
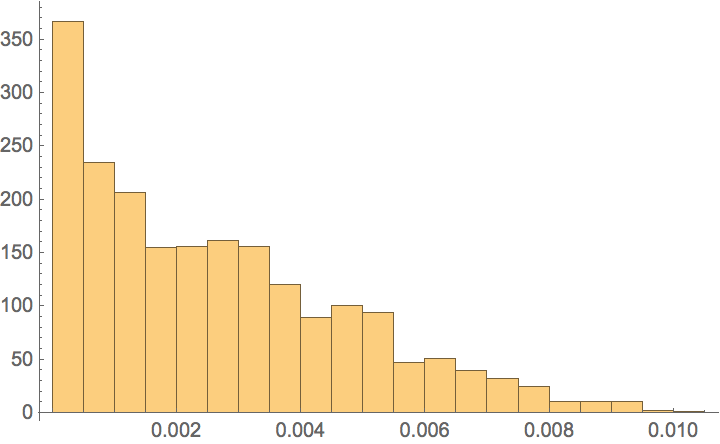
RegionMeasure /@ MeshPrimitives[ DiscretizeRegion@RegionIntersection[Sphere /@ {-#, #}], 1] &@ {0.09666984222273534`, 0.3622850077710253`, 0.33076353297934696`} // Histogram I can limit size of these gaps with MaxCellMeasureoption, but it doesn't really remove the problem involving non-uniformity:
RegionMeasure /@ MeshPrimitives[ DiscretizeRegion[RegionIntersection[Sphere /@ {-#, #}], MaxCellMeasure -> {"Length" -> .01}], 1] &@ {0.09666984222273534`, 0.3622850077710253`, 0.33076353297934696`} // Histogram What other methods there are to improve quality of such discretizations? Note that spheres are just an example; I'm looking for a general solution for intersections of arbitrary polynomial surfaces.
EDIT: I think this can be accomplished with SemialgebraicComponentInstances and NDSolve, but it's work in progress.