10
$\begingroup$

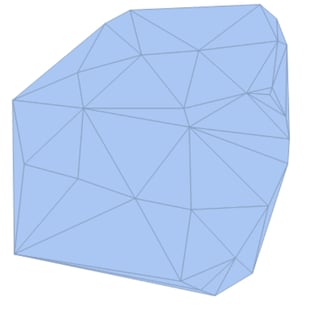
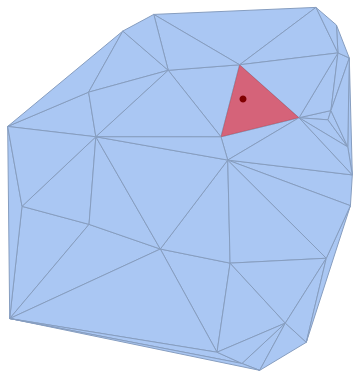
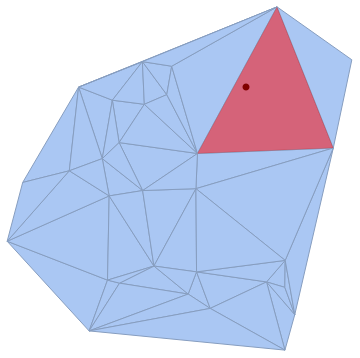
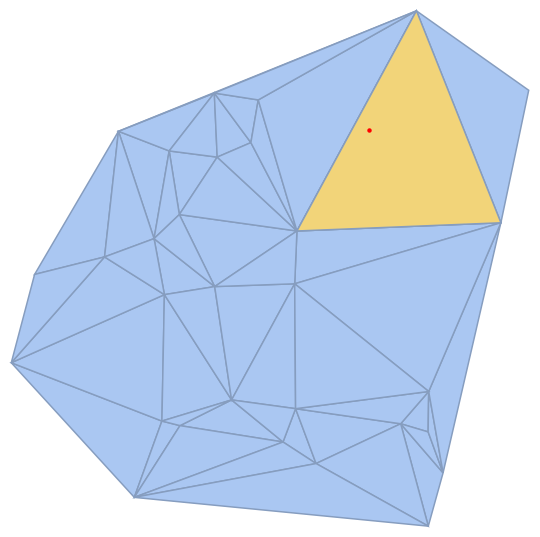
I have a set of points pts1 and a point redPts as below:-

pts1 = BlockRandom[SeedRandom[7]; RandomReal[1, {30, 2}]]; plot1 = DelaunayMesh[pts1] redPts = {0.68, 0.75} plot2a = ListPlot[pts1, AspectRatio -> 1]; plot2b = ListPlot[{redPts}, PlotStyle -> Red]; Show[plot2a, plot2b]

enter image description here enter image description here

As you can see, redPts must lie inside a face of the Delaunay Mesh. I want to have the coordinates of the 3 vertexes of that face. What can I do?

One of my solutions is to check the distance of "all points v.s. red point" and then pick the 3 points with the smallest distance. But is that possible to make use of the DelaunayMesh?

Many thanks!

Improve this question
$\endgroup$

2 Answers 2

Reset to default
5
$\begingroup$

Update: As noted by Henrik and Rahul the original answer is not the correct approach. An alternative method that gives the correct polygon containing redPt is based on using Graphics`PolygonUtils`InPolygonQ:

ClearAll[f] f[r_, p_] := Pick[#, Graphics`PolygonUtils`InPolygonQ[#, p] & /@ #] &@ MeshPrimitives[r, 2]; Show[plot1, Graphics[{PointSize[Large], Point@redPt, Opacity[.5, Red], f[plot1, redPt]}]]

enter image description here

To get the coordinates, use 

f[plot1, redPt][[1, 1]]

{{0.67033, 0.84245}, {0.620283, 0.648944}, {0.829905, 0.700287}}

Using Henrik's example (R):

Show[R, Graphics[{PointSize[Large], Point@redPt, Opacity[.5, Red], f[R, redPt]}]]

enter image description here

Original (incorrect) answer:

Nearest[MeshCoordinates[plot1], redPts, 3]
Improve this answer
$\endgroup$
7
  • $\begingroup$ This is incorrect; see Henrik Schumacher's answer. $\endgroup$ Commented Jun 17, 2018 at 12:23
  • $\begingroup$ Thank you @Rahul. $\endgroup$ Commented Jun 17, 2018 at 15:45
  • $\begingroup$ @HMC, the original accepted version of this answer is incorrect as noted by Rahul and Henrik. I updated with a version that gives the correct answer. But you might reconsider your acceptance since the accepted version was incorrect. $\endgroup$ Commented Jun 18, 2018 at 5:57
  • 1
    $\begingroup$ Ah, finding another working solution is even better than deleting the post. =) I'd like to mention that your solution tests the point against each triangle and thus has complexity $O(F)$ (where $F$ is the number of faces). There are certainly cleverer ways to find the right triangle, e.g. walks along edges backed up by some BSP-based heuristic for the initial edge. $\endgroup$ Commented Jun 18, 2018 at 8:49
  • $\begingroup$ I expected Region`Mesh`MeshNearestCellIndex to do such a clever thing. While it is two orders of magnitude faster for Delaunay meshes with up to 80000 vertices, it starts getting super-linear growing runtime for larger meshes. (This could also be memory related and not related to the actual algorithm). $\endgroup$ Commented Jun 18, 2018 at 8:51
9
$\begingroup$

Finding the correct triangle is a very delicate business. See for example:

pts1 = BlockRandom[SeedRandom[1]; RandomReal[1, {30, 2}]]; R = DelaunayMesh[pts1]; redPt = {0.68, 0.75}; idx = Nearest[MeshCoordinates[R] -> Automatic, redPt, 3]; r = Max@Nearest[MeshCoordinates[R] -> "Distance", redPt, 3]; i = Position[Through[(RegionMember /@ MeshPrimitives[R, 2])[redPt]], True][[1, 1]]; Show[ HighlightMesh[R, Join[Thread[{0, idx}], {{2, i}}]], Graphics[{ Red, Point@redPt, Circle[redPt, r] }], PlotRange -> All ]

enter image description here

Fortunately, there seems to be a built-in but undocumented function for this task:

j = Region`Mesh`MeshNearestCellIndex[R, redPt]; MeshPrimitives[R, j] Show[ HighlightMesh[R, j], Graphics[{Red, Point[redPt]}] ]

Polygon[{{0.925275, 0.578056}, {0.767697, 0.973336}, {0.544772, 0.562659}}]

enter image description here

Improve this answer
$\endgroup$
1
  • $\begingroup$ Wow, great example showing that Nearest is not always correct! $\endgroup$ Commented Jun 17, 2018 at 10:04

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.