12
$\begingroup$

Assume I have a ClassifierFunction object learned like this:

classifier = Classify[trainSet, Method -> "DecisionTree"]

Then how can I extract the actual decision tree structure from the result?

Here an example:

fn[n_] := Which[n < 1, 1, 1 <= n < 2, 2, 2 <= n, 3]; data = Table[(r = RandomReal[{0, 4}]; r -> fn[r]), {i, 1, 1000}]; c = Classify[data, Method -> "DecisionTree"];
Improve this question
$\endgroup$
7
  • $\begingroup$ Hard to answer without a concrete minimal example for trainSet. $\endgroup$ Commented Aug 27, 2018 at 8:33
  • $\begingroup$ How about this step function with a branching in decision? fn[n_] := Which[n < 1, 1, 1 <= n < 2, 2, 2 <= n, 3];. Data generated as data = Table[(r = RandomReal[{0, 4}]; r -> fn[r, 1, 2, 3]), {i, 1, 1000}]; and classifying using c = Classify[data, Method -> "DecisionTree"]; then trying to visuallize using c[[1, "Model", "Tree"]] $\endgroup$ Commented Sep 12, 2018 at 12:36
  • $\begingroup$ @HenrikSchumacher - I see an output like this See an output like this for the question <|FeatureIndices->RawArray[Integer16,<2>],NumericalThresholds->RawArray[Real32,<2>],NominalSplits->{},Children->RawArray[Integer16,<2,2>],LeafValues->RawArray[UnsignedInteger16,<3,3>],RootIndex->2,NominalDimension->0|>` with classifier[[1, "Model", "Tree"]] . Can be improved further? $\endgroup$ Commented Sep 12, 2018 at 12:42
  • 1
    $\begingroup$ Are you interested in visualizing the Decision Trees made by Classify, or you just want to visualize a Decision Tree over some data? $\endgroup$ Commented Sep 12, 2018 at 13:22
  • $\begingroup$ @AntonAntonov - I was curious about visualizing the DecisionTrees made by Classify... Your answer in this thread was what I was looking for $\endgroup$ Commented Sep 14, 2018 at 15:18

2 Answers 2

Reset to default
8
$\begingroup$

Here is one way to visualize/interpret Classify's tree structure from Henrik Schumacher's answer.

SeedRandom[432] fn[n_] := Which[n < 1, 1, 1 <= n < 2, 2, 2 <= n, 3]; data = Table[(r = RandomReal[{0, 4}]; r -> fn[r]), {i, 1, 1000}]; c = Classify[data, Method -> "DecisionTree"]; tree = c[[1, "Model", "Tree"]]; fromRawArray[a_RawArray] := Developer`FromRawArray[a]; fromRawArray[a_] := a; Map[Normal, fromRawArray /@ tree[[1]]] (* <|"FeatureIndices" -> {1, 1}, "NumericalThresholds" -> {-0.894867, -0.0252423}, "NominalSplits" -> {}, "Children" -> {{-2, -3}, {1, -1}}, "LeafValues" -> {{1, 1, 508}, {246, 1, 1}, {1, 249, 1}}, "RootIndex" -> 2, "NominalDimension" -> 0|> *) Import["https://raw.githubusercontent.com/antononcube/MathematicaForPrediction/master/AVCDecisionTreeForest.m"] dtree = BuildDecisionTree[List @@@ data] (* {{0.374931, 1.9972, 1, Number, 1000}, {{0.499981, 1.0175, 1, Number, 493}, {{{245, 1}}}, {{{248, 2}}}}, {{{507, 3}}}} *) LayeredGraphPlot[DecisionTreeToRules[dtree], VertexLabeling -> True]

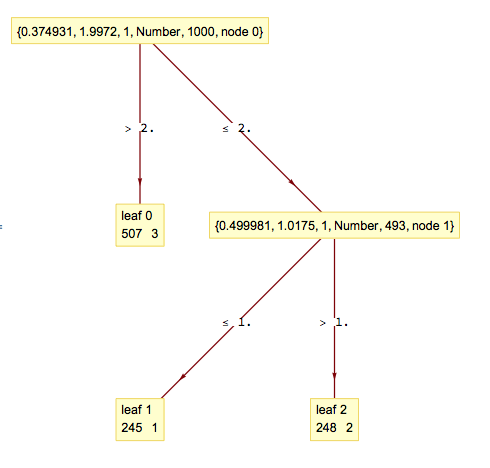
enter image description here

There is a discrepancy of 1 in the obtained values, but otherwise the second tree seems to approximate Classify's one well. The splitting thresholds of Classify's tree a most likely obtained over the data being transformed with some embedding/hashing/normalization.

Improve this answer
$\endgroup$
3
  • 1
    $\begingroup$ Note: this visualization is NOT that of Classify[], but that of BuildDecisionTree[] $\endgroup$ Commented Sep 15, 2018 at 6:40
  • 1
    $\begingroup$ @myaccount_ram I thought this is clear from my explanations, but I guess it isn't... $\endgroup$ Commented Sep 15, 2018 at 12:49
  • $\begingroup$ I challenge the downvoter to explain the reasons for the downvote. :) $\endgroup$ Commented Feb 15 at 21:48
5
$\begingroup$

In general, many objects generated by Mathematica can be inspected by trying things of the form InputForm[classifier] or classifier[string] with string being one of the elements of classifier["Properties"]. Recently implemented objects such as ClassifierFunction are mere wrappers for well-structured Associations (thumbs up for this approach!), so classifier[[1]] can be very revealing.

The following reveals that

tree = c[[1, "Model", "Tree"]]

is another such object (with head MachineLearning`DecisionTree).

Inspecting

tree[[1]]

reveals that MachineLearning`DecisionTree are partially composed of RawArrays. These can be converted to usual integer arrays as follows:

fromRawArray[a_RawArray] := Developer`FromRawArray[a]; fromRawArray[a_] := a; fromRawArray /@ tree[[1]]

<|"FeatureIndices" -> {1, 1}, "NumericalThresholds" -> {0.402823, 0.82983}, "NominalSplits" -> {}, "Children" -> {{-1, 2}, {-2, -3}}, "LeafValues" -> {{619, 1, 1}, {1, 130, 1}, {1, 1, 254}}, "RootIndex" -> 1, "NominalDimension" -> 0|>

But I cannot tell you how to interpret this data. I would have to learn first what a decision tree is and how it is constructed...

Improve this answer
$\endgroup$
0

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.