7
$\begingroup$

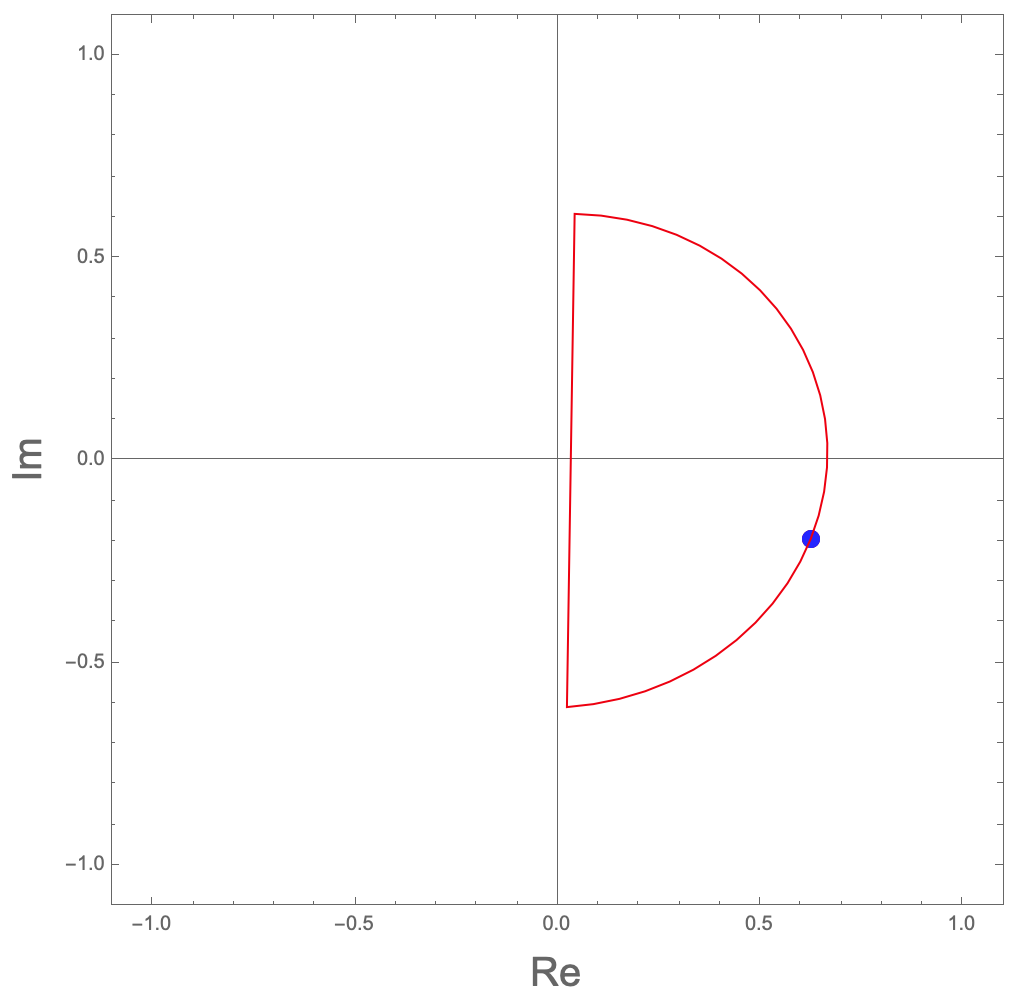
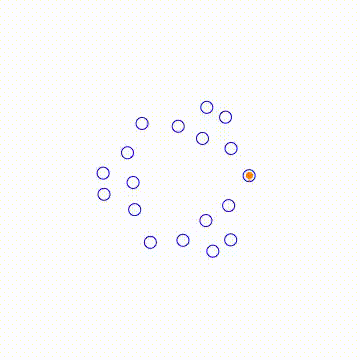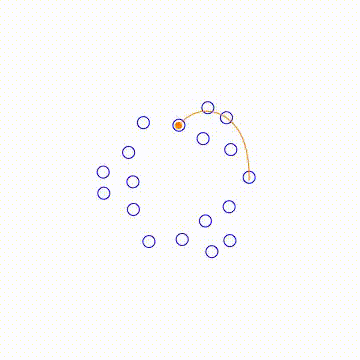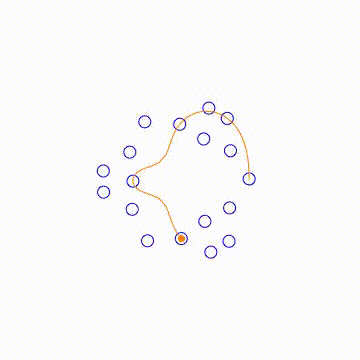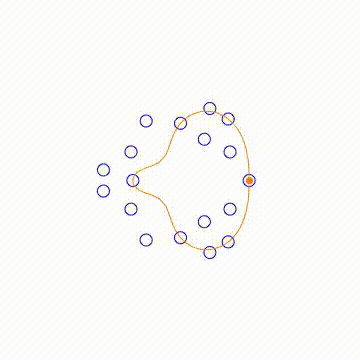
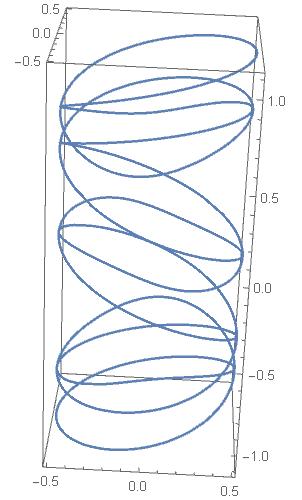
Currently, Mathematica treats function which has branch cuts; $\log(z)$,$\sqrt[n]{z}$, etc, by taking its principal value. This may cause a problem in Contour integration when the path of integration walks over the branch cut. This may be fixed by a wise implementation of the Integrate function. But it is still a problem in my case. That is I want to visualize how curves in a complex plane are transformed by complex functions. For example, when a point in a complex plane moves around an origin twice, I want to see the point projected by $\sqrt(z)$ move around an origin once. But Mathematica's Sqrt makes the projected point jumps discontinuously when a point walk across the branch cut as seen in the attached picture.

I think this problem can be resolved by making every complex calculation to avoid taking modulo $2\pi$ to the phase of a complex value until the last moment. So the internal representation of complex values should be polar form and there must be a wise mechanism to decide when to do modulo $2\pi$ operation to its phase.

What do you think about this idea? Is there a way to visualize the "natural path" of a projected point by complex functions that have branch cuts?

Thank you. enter image description here

EDIT Thanks to Dominic and J. M. will be back soon, I finally achieved what I want. Thank both of you!

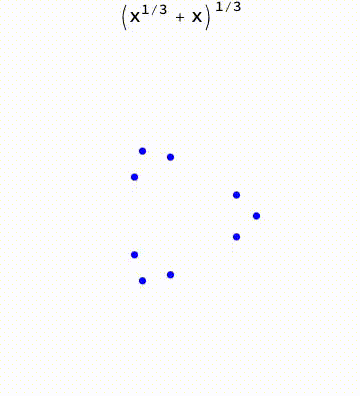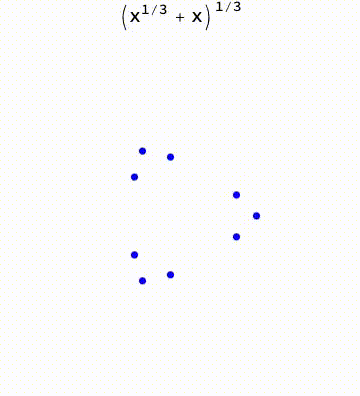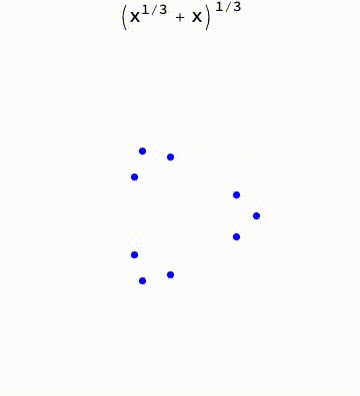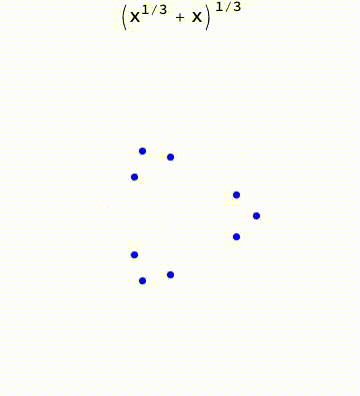
BranchRootsMod[exp_] := Module[ {p, f, e, k, t}, If[Head[exp] === List, t = BranchRootsMod /@ exp; , p = Position[exp, _^_Rational]; If[Length[p] > 0, f = First[p]; If[Length[f] == 0, e = exp; k = e /. _^r_Rational :> 1/r; t = Table[root[First[e], 1/k]*Exp[I ( 2 \[Pi] i)/k], {i, 0, k - 1}]; , e = Extract[exp, f]; k = e /. _^r_Rational :> 1/r; t = Table[ReplacePart[exp, f -> root[First[e], 1/k]*Exp[I ( 2 \[Pi] i)/k]], {i, 0, k - 1}]; ]; , t = exp; ]; ]; t ]; BranchRoots[exp_] := Module[{e = (FixedPoint[BranchRootsMod, exp] /. root -> Power)}, If[Head[e] === List, Flatten[e], e]]; ProjectedTrajectory[exp_, var_, traj_, range_] := Module[{w, t, trajd, wd, func, sol}, func = Simplify[First[GroebnerBasis[{w == exp}, {var, w}]]]; t = range[[1]]; trajd = D[traj, t]; wd = w'[ t] == ((-(D[func, var]/D[func, w]) trajd) /. {w -> w[t], var -> traj}); sol = First[ NDSolve[{wd, w[range[[2]]] == exp /. (var :> (traj /. t -> range[[2]]))}, w, {t, range[[2]], range[[3]]}]]; w /. sol ] tmax = 12 \[Pi]; exp = (x^(1/3) + x^(1/2) - 0.5)^(1/3); traj = ProjectedTrajectory[exp, x, Exp[I t], {t, 0, 2*tmax}]; list = Table[Through[{Re, Im}@traj[t]], {t, 0, tmax, tmax/ 100}]; Manipulate[ Module[{pts}, pts = Through[{Re, Im}@#] & /@ BranchRoots[exp] /. x -> Exp[I t]; Graphics[ { {Blue, Circle[#, 0.1]} & /@ pts, {Orange, PointSize[0.02], Point[Through[{Re, Im}@traj[t]]]}, {Orange, Line@list[[;; Floor[100*t/tmax]]]} }, PlotRange -> {{-3, 3}, {-3, 3}} ]], {t, 0, tmax} ]

enter image description here

Improve this question
$\endgroup$
1

2 Answers 2

Reset to default
5
$\begingroup$

I've been working with multivalued functions for a while and without a doubt the best way I have found to avoid branch cuts, in particular when integrating over multivalued functions, is to construct an analytically-continuous version of the function over the desired path. For algebraic functions, this is easy: convert it to its algebraic form. For example $w(x)=(x+x^{1/3})^{1/3}$ in its algebraic form is equivalent to: $f(x,w)=w^9-3w^6x+3 w^3 x^2-x^3-x=0$. Now suppose I wish to construct an analtyically-continuous version of this multivalued function over the path $z(t)=1/2 e^{it}$, then we have: $$ \frac{dw}{dt}=-\frac{f_x}{f_w}\frac{dx}{dt} $$ Now solve the IVP:
$$ \frac{dw}{dt}=-\frac{f_x}{f_w}\frac{dx}{dt};\quad w(t_0)=w_0 $$ so let's pick an initial starting point say one of the roots of $w(1/2)=w_0$. Then use the following code (converted to w and z):

r = 1/2; theFunction = w^9 - 3 w^6 z + 3 w^3 z^2 - z^3 - z; tStart = 0; tEnd = 18 Pi; myz[t_] := r Exp[I t]; wStart = (r + r^(1/3))^(1/3); wDeriv = w'[ t] == ((-(D[theFunction, z]/ D[theFunction, w]) (I r Exp[I t])) /. {w -> w[t], z -> myz[t]}) theSolution = First[NDSolve[{wDeriv, w[tStart] == wStart}, w, {t, tStart, tEnd}]]; theTrace[t_] := Evaluate[Flatten[w[t] /. theSolution]]; ParametricPlot3D[{Re@myz[t], Im@myz[t], Re@theTrace[t]}, {t, tStart, tEnd}]

theTrace[t] now respresents an anlaytically-continuous version of the function devoid of branch cuts and can now for example be used to NIntegrate over the function over this path. The plot below shows a smooth path though this 9-degree function: enter image description here

Improve this answer
$\endgroup$
4
  • $\begingroup$ Thank you very much, Dominic. Can I ask you one more thing: How can I convert a function like $x^{1/2} + x^{1/3}$ to its algebraic form? $\endgroup$ Commented Nov 24, 2019 at 3:43
  • $\begingroup$ That's $w^6=x(x^3+x^2)^6$. However there are limits to simple algebraic mainpulation. In those cases, would need to construct analytically-continuous version of each multivalued part of the expression, for example, above, letting $w_1=x^{1/2}$ and $w_2=x^{1/3}$ and solving two ivps and then adding them. $\endgroup$ Commented Nov 24, 2019 at 9:01
  • 3
    $\begingroup$ @Hayashi and Dominic: you can use GroebnerBasis[] for that, e.g. Simplify[First[GroebnerBasis[{w == (x + x^(1/3))^(1/3)}, {x, w}]]] yields -w^9 + x + 3 w^6 x - 3 w^3 x^2 + x^3. Due to the nature of the method, it might take a while if the function to be "algebraicized" is fairly complicated, but it mostly works well. On that note, Simplify[First[GroebnerBasis[{w == x^(1/2) + x^(1/3)}, {x, w}]]] gives a result that is quite different from Dominic's comment. $\endgroup$ Commented Nov 29, 2019 at 23:01
  • $\begingroup$ Thanks for pointing that out to me J.M. I made a mistake with exponents above. It's more complicated and I don't see how to convert it to the GroebnerBasis with simple algebraic manipulations by hand. $\endgroup$ Commented Nov 30, 2019 at 13:52
3
$\begingroup$

When I asked this question I was more optimistic about this problem. But it turned out this is a really hard problem. Avoid doing modulo 2đťś‹ operation didn't work. It would work when an expression is made only by multiplication and powers, but addition combines two angles in a complicated way and it makes this approach difficult. So my original idea failed.

Instead of obtaining a continuous movement of a single point, I managed to make a program that draws multiple points from different branches. It looks nice if all points are colored with the same color, but when different colors are used for each point, this problem shows up as a sudden switch of colors. 

BranchRootsMod[exp_] := Module[ {p, f, e, k, t}, If[Head[exp] === List, t = BranchRootsMod /@ exp; , p = Position[exp, _^_Rational]; If[Length[p] > 0, f = First[p]; If[Length[f] == 0, e = exp; k = e /. _^r_Rational :> 1/r; t = Table[root[First[e], 1/k]*Exp[I ( 2 \[Pi] i)/k], {i, 0, k - 1}]; , e = Extract[exp, f]; k = e /. _^r_Rational :> 1/r; t = Table[ReplacePart[exp, f -> root[First[e], 1/k]*Exp[I ( 2 \[Pi] i)/k]], {i, 0, k - 1}]; ]; , t = exp; ]; ]; t ]; BranchRoots[exp_] := Module[{e = (FixedPoint[BranchRootsMod, exp] /. root -> Power)}, If[Head[e] === List, Flatten[e], e]]; Manipulate[ Module[{cl = ColorData[97, "ColorList"], list = (Through[{Re, Im}@#] & /@ (BranchRoots[exp]) /. x :> Exp[I \[Theta]]), glist}, glist = Table[{Blue, PointSize[0.02], Point[list[[k]]]}, {k, Length[list]}]; Labeled[ Graphics[glist, PlotRange -> {{-3, 3}, {-3, 3}}], Style[exp, 20], Top ] ] , {\[Theta], -12 \[Pi], 12 \[Pi]}, {exp, (x^(1/3) + x)^(1/3)} ]

enter image description here enter image description here

Improve this answer
$\endgroup$
1
  • 3
    $\begingroup$ Right. This indicates that the individual parametrized root functions will swap at points of multiplicity (which is the branch cut issue all over again). $\endgroup$ Commented Nov 24, 2019 at 16:06

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.