0
$\begingroup$

I have this equation and I want to draw the contour plot. 

-1.94178*10^24 H Te^0.5 - ( 3.2*10^-9 (7.33376*10^27 Te^(7/2) + 4.66533*10^24 Ti^(7/2)))/H + 7.68161*10^40 H ((5.41*10^-15 E^(-148/Ti))/Ti^(3/2) + ( 2.00122*10^-10 E^(-(( 53.124 (1 - (-0.059357 Ti + 0.0010404 Ti^2 - 9.1653*10^-6 Ti^3)/( 1 + 0.20165 Ti + 0.0027621 Ti^2 + 9.8305*10^-7 Ti^3))^(1/3))/ Ti^(1/3))))/( Ti^(2/3) (1 - (-0.059357 Ti + 0.0010404 Ti^2 - 9.1653*10^-6 Ti^3)/( 1 + 0.20165 Ti + 0.0027621 Ti^2 + 9.8305*10^-7 Ti^3))^(5/6)))

I have used this code to draw the contourplot.

H0 = 0.042; xyz = {} Do[s0 = t0 /. {Ti -> ti, Te -> te}; h = H /. FindRoot[s0 == 0, {H, H0}]; xyz = Append[xyz, {ti, te, h}];, {ti, 1, 200}, {te, 1, 40}] c = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}; f0 = ListContourPlot[xyz, ColorFunction -> "IslandColors", Contours -> c , FrameLabel -> {Style[ "\!\(\*SubscriptBox[\(T\), \(i\)]\)(keV)", FontSize -> 14, FontFamily -> "Times"], Style["\!\(\*SubscriptBox[\(T\), \(e\)]\)(keV)", FontSize -> 14, FontFamily -> "Times"]}, ContourLabels -> (Text[#3, {#2, #2}, Background -> White] &), LabelStyle -> {Directive[Black, Bold], (FontSize -> 16), FontFamily -> "Times"}, ]

the problem is when i draw the plot there are some duplicate lines i don't want them to be in plot. how can i remove them. here is the picture of the plot.contourplot

Improve this question
$\endgroup$

1 Answer 1

Reset to default
3
$\begingroup$

Why not just using ContourPlot?

eq = -1.94178*10^24*H*Te^0.5 - (3.2*(7.33376*10^27*Te^(7/2) + 4.66533*10^24*Ti^(7/2)))/ (10^9*H) + 7.68161*10^40*H*(5.41/((10^15*E^(148/Ti))*Ti^(3/2)) + 2.00122/((10^10*E^((53.124*(1 - (-0.059357*Ti + 0.0010404*Ti^2 - (9.1653*Ti^3)/10^6)/ (1 + 0.20165*Ti + 0.0027621*Ti^2 + (9.8305*Ti^3)/10^7))^(1/3))/Ti^(1/3)))* (Ti^(2/3)*(1 - (-0.059357*Ti + 0.0010404*Ti^2 - (9.1653*Ti^3)/10^6)/ (1 + 0.20165*Ti + 0.0027621*Ti^2 + (9.8305*Ti^3)/10^7))^(5/6)))); sol = H /. Solve[eq == 0, H] // Simplify;

Now we can plot:

 ContourPlot[sol[[2]], {Ti, 1, 2000}, {Te, 1, 200}, Contours -> Range[15], ColorFunction -> "IslandColors", PlotPoints -> 100, FrameLabel -> {Style["\!\(\*SubscriptBox[\(T\), \(i\)]\)(keV)", FontSize -> 14, FontFamily -> "Times"], Style["\!\(\*SubscriptBox[\(T\), \(e\)]\)(keV)", FontSize -> 14, FontFamily -> "Times"]}, LabelStyle -> {Directive[Black, Bold], (FontSize -> 16), FontFamily -> "Times"}]

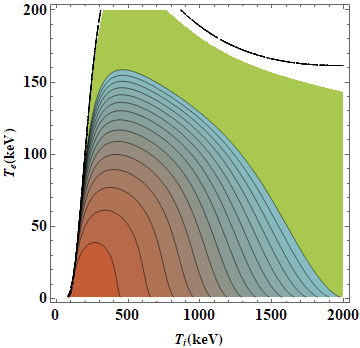
enter image description here

I plotted sol[[2]] because sol[[1]] corresponds to negative contour levels.

EDIT

It is possible also plot this eq in 3D:

ContourPlot3D[eq == 0, {Ti, 1, 2000}, {Te, 1, 200}, {H, 1, 15}, MeshFunctions -> (#3 &), Mesh -> {Range[15]}, AxesLabel -> {Style["\!\(\*SubscriptBox[\(T\), \(i\)]\)(keV)", FontSize -> 14, FontFamily -> "Times"], Style["\!\(\*SubscriptBox[\(T\), \(e\)]\)(keV)", FontSize -> 14, FontFamily -> "Times"], Style["H", FontSize -> 14, FontFamily -> "Times"]}, LabelStyle -> Directive[Black, Bold], BaseStyle -> Directive[Black, Bold, FontSize -> 14, FontFamily -> "Times"], ColorFunction -> (ColorData["IslandColors"][#3] &)]

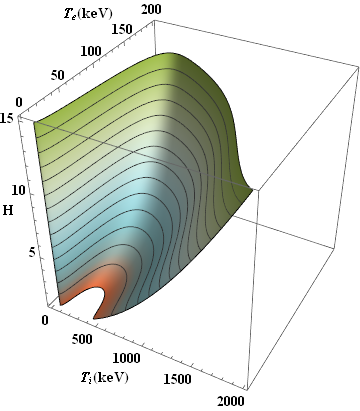
enter image description here

EDIT 2

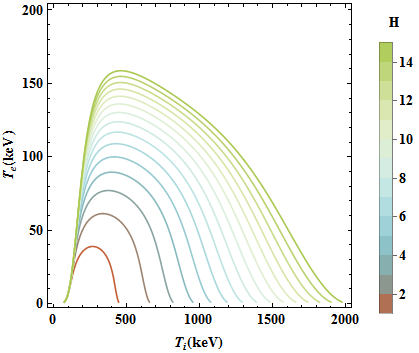
Without solving original equation eq for H, we can plot contours of eq == 0 for specific values of H:

ClearAll[eq]; eq[H_] := -1.94178*10^24*H*Te^0.5 - (3.2*(7.33376*10^27*Te^(7/2) + 4.66533*10^24*Ti^(7/2)))/ (10^9*H) + 7.68161*10^40*H*(5.41/((10^15*E^(148/Ti))*Ti^(3/2)) + 2.00122/((10^10*E^((53.124*(1 - (-0.059357*Ti + 0.0010404*Ti^2 - (9.1653*Ti^3)/10^6)/ (1 + 0.20165*Ti + 0.0027621*Ti^2 + (9.8305*Ti^3)/10^7))^(1/3))/Ti^(1/3)))* (Ti^(2/3)*(1 - (-0.059357*Ti + 0.0010404*Ti^2 - (9.1653*Ti^3)/10^6)/ (1 + 0.20165*Ti + 0.0027621*Ti^2 + (9.8305*Ti^3)/10^7))^(5/6)))); ContourPlot[Evaluate@eq[Range[15]], {Ti, 1, 2000}, {Te, 1, 200}, ContourStyle -> ColorData["IslandColors"] /@ Rescale[Range[15]], PlotLegends -> BarLegend[{"IslandColors", {1, 15}}, Range[15], LegendLabel -> "H", LegendMarkerSize -> 300, LabelStyle -> Directive[Black, Bold, FontFamily -> "Times", 14]], FrameStyle -> Directive[Black, Bold, 14, FontFamily -> "Times"], FrameLabel -> {"\!\(\*SubscriptBox[\(T\), \(i\)]\)(keV)", "\!\(\*SubscriptBox[\(T\), \(e\)]\)(keV)"}, PlotPoints -> 50]

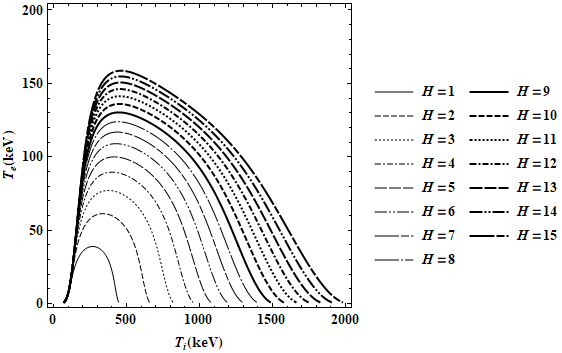
enter image description here

For b&w plot one can use ContourStyle option and adjust thickness and dashing (here I borrowed dashing patterns from PlotTheme -> "Monochrome" and added two types of thickness):

ContourPlot[Evaluate@eq[Range[15]], {Ti, 1, 2000}, {Te, 1, 200}, ContourStyle -> Directive @@@ Tuples[{{Black}, {Thickness[Medium], Thickness[Large]}, {AbsoluteDashing[{}], AbsoluteDashing[{6, 2}], AbsoluteDashing[{2, 2}], AbsoluteDashing[{6, 2, 2, 2}], AbsoluteDashing[{12, 2}], AbsoluteDashing[{12, 2, 2, 2, 2, 2}], AbsoluteDashing[{24, 2, 8, 2}], AbsoluteDashing[{24, 2, 2, 2}]}}], PlotLegends -> (Row[{HoldForm@H, "\[ThinSpace]=\[ThinSpace]", #}] & /@ Range[15]), FrameStyle -> Directive[Black, Bold, 14, FontFamily -> "Times"], FrameLabel -> {"\!\(\*SubscriptBox[\(T\), \(i\)]\)(keV)", "\!\(\*SubscriptBox[\(T\), \(e\)]\)(keV)"}, PlotPoints -> 50, LabelStyle -> Directive[Black, Bold, FontFamily -> "Times", 14]]

enter image description here

Improve this answer
$\endgroup$
10
  • $\begingroup$ Thank ypu very much for your help. it really saved me. $\endgroup$ Commented Dec 11, 2019 at 12:16
  • $\begingroup$ I added possible use of ContourPlot3D, please see edited part. $\endgroup$ Commented Dec 11, 2019 at 12:29
  • $\begingroup$ thank you very much kind regards. i had some other questions: why did you put plot points? $\endgroup$ Commented Dec 11, 2019 at 12:37
  • $\begingroup$ PlotPoints is usually used to make plot more smooth, it may depend on particular plot whether it should be used. Mathematica uses adaptive algorithm to find sufficient number of sample points, but we can sometimes help it. $\endgroup$ Commented Dec 11, 2019 at 13:04
  • 1
    $\begingroup$ For b&w plot you can use either PlotTheme -> "Monochrome" (with lesser number of contours because it has limited number of dashing patterns) or set ContourStyle option with appropriate combinations of tickness/dashing, I added b&w plot. $\endgroup$ Commented Dec 12, 2019 at 10:53

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.