Creating Python's Polar Heat Map Equivalent (effectively ListDensityPolarPlot)

I have a set of data that is in the form

{{\[Theta], \[Phi], r},....} 

Or to make it simpler:

data={{0, 0, 3.3102}, {0, 2, 3.3102}, ..., {10, 90, 4.084}} 

Alternatively, a data set can be generated by using:

data=Flatten[Table[{th,phi,RandomReal[100]},{th,0,45,2},{phi,0,90,2}],1]; 

Now I want to plot this data in a polar plot to get something equivalent to: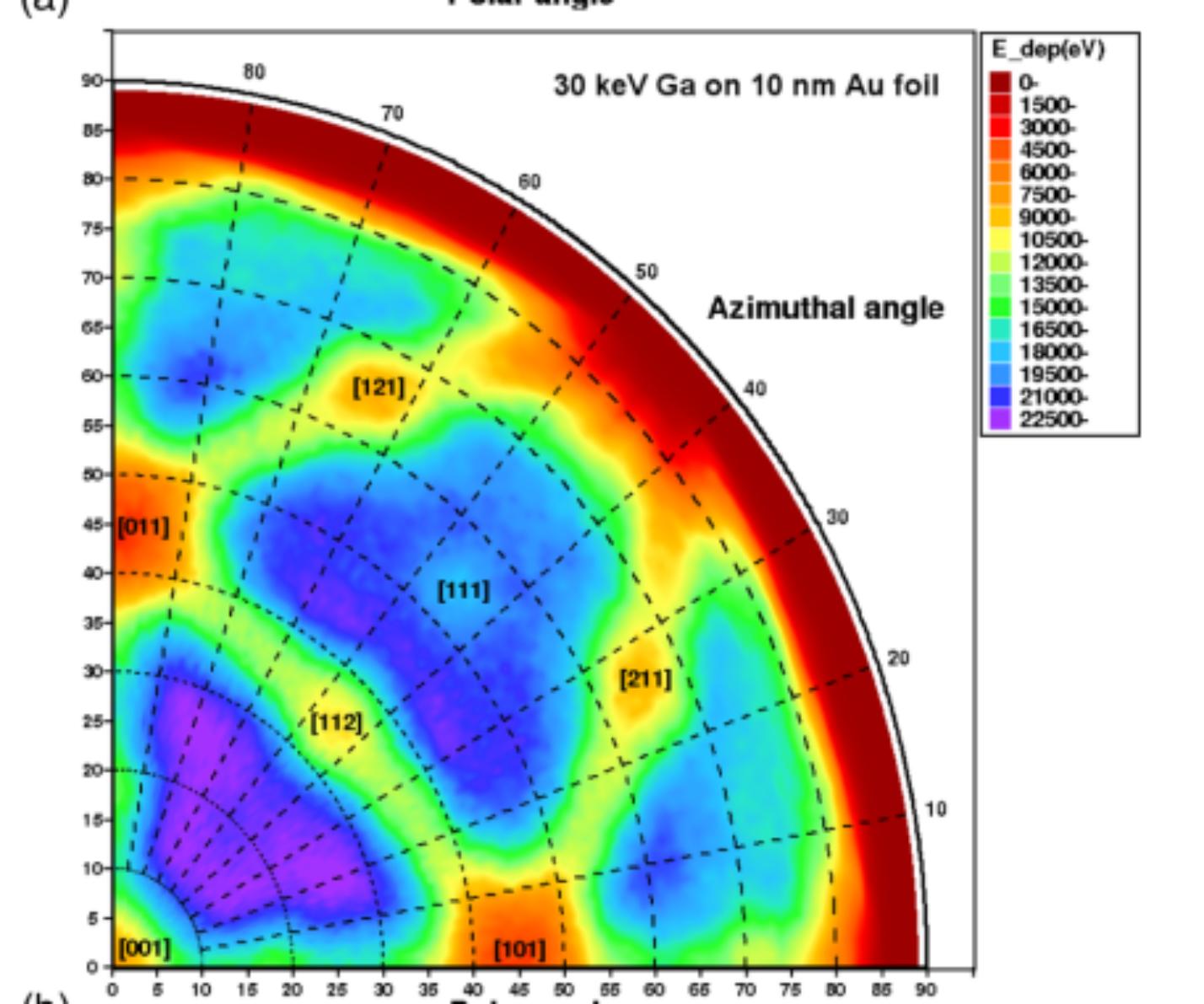

Where the text in the picture referring to different crystal planes is not important. To generate a uniform density plot, there should be some interpolation between data points but I guess that is not necessary as I can always do that in preprocessing of the data points. Now this is somewhat easily generated by using python, however I am looking for a way to generate such a plot in mathematica in attempts to keep layout consistency between my other plots.

I can easily generate a ListDensityPlot using:

ListDensityPlot[data] 

That looks like (with some legends manipulation and graphics options tweaked to make it look "more presentable"):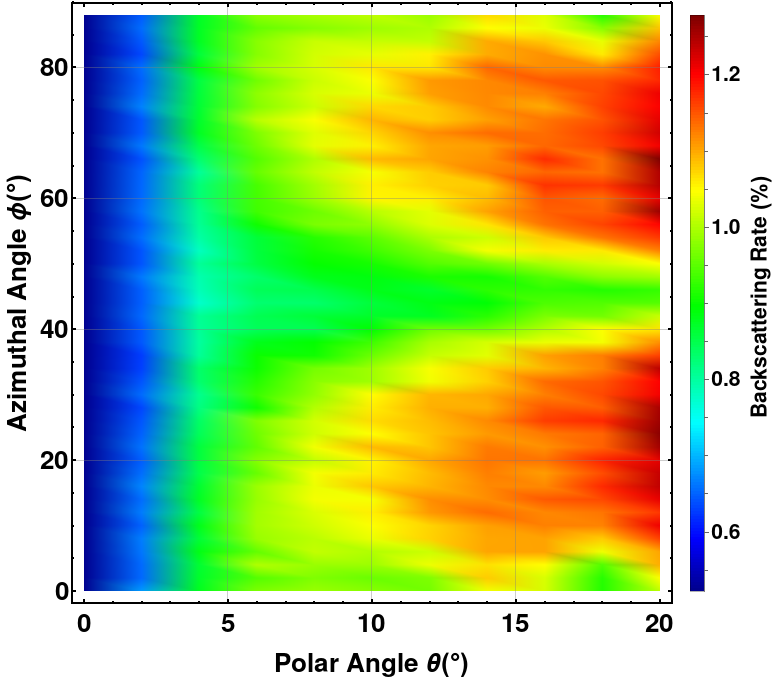

I managed to convert the rectangular plot to a circular one using transfromation of coordinates i.e.

N[{#[[1]] Cos[#[[2]]], #[[1]] Sin[#[[2]]], #[[3]]}] & /@data 

Not a 100% sure that this is correct to be honest, but I guess it is the right approach i.e. convert coordinates

But I still don't know how to add the grid lines properly, the custom legend i.e. Azimuthal Angle I guess I can always add afterwards by hand but it would be appreciated to add it while plotting too