I am total beginner in Mathematica. Don't know a thing. I need to draw some diagrams for showing the conformal nature of map $w=e^z$.
I need to draw some contours in $z$-plane; e.g., horizontal line, vertical line, 45 degree line and unit circle. Then I need to obtain the mapped curves in $w$-plane where $u$ and $v$ are functions of $x$ and $y$.
I have no idea how to do this? Please help me.
Reply to the comment.
Use MeshShading to fill the region.
expr1 = {x, y}; expr2 = With[{z = x + I*y}, E^z // ReIm // ComplexExpand]; ParametricPlot[#, {x, -4, 4}, {y, -4, 4}, MeshFunctions -> {#3 &, #4 &, #4 - #3 &, Sqrt[#3^2 + #4^2] &}, Mesh -> {{1}, {1}, {0}, {1}}, MeshShading -> {{{{Red, None}, {None, None}}, {{Red, None}, {None, None}}}, {{{None, None}, {None, None}}, {{None, None}, {None, None}}}}, MeshStyle -> {{Thick, Red, Opacity[1]}, {Thick, Green, Opacity[1]}, {Thick, Blue, Opacity[1]}, {Thick, Yellow, Opacity[1]}}, Axes -> False, PlotRange -> 4, BoundaryStyle -> None, LabelStyle -> {FontFamily -> "Times", Blue}, PlotPoints -> 80, PlotStyle -> None] & /@ {expr1, expr2} // GraphicsRow 
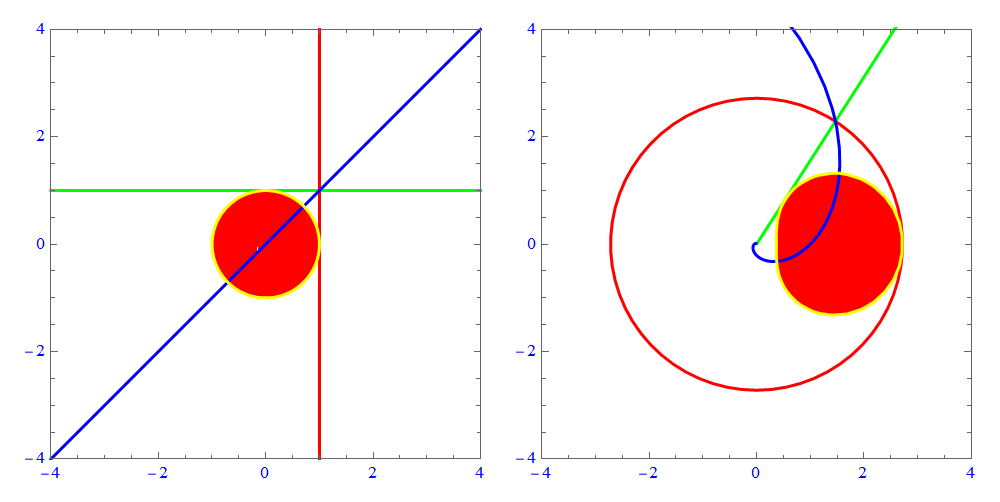
Simplify
expr1 = {x, y}; expr2 = With[{z = x + I*y}, E^z // ReIm // ComplexExpand]; ParametricPlot[#, {x, -4, 4}, {y, -4, 4}, MeshFunctions -> {#3 &, #4 &, #4 - #3 &, Sqrt[#3^2 + #4^2] &}, Mesh -> {{1}, {1}, {0}, {1}}, MeshStyle -> {{Thick, Red, Opacity[1]}, {Thick, Green, Opacity[1]}, {Thick, Blue, Opacity[1]}, {Thick, Yellow, Opacity[1]}}, Axes -> False, PlotRange -> 4, BoundaryStyle -> None, LabelStyle -> {FontFamily -> "Times", Blue}, PlotPoints -> 80, PlotStyle -> None] & /@ {expr1, expr2} // GraphicsRow 
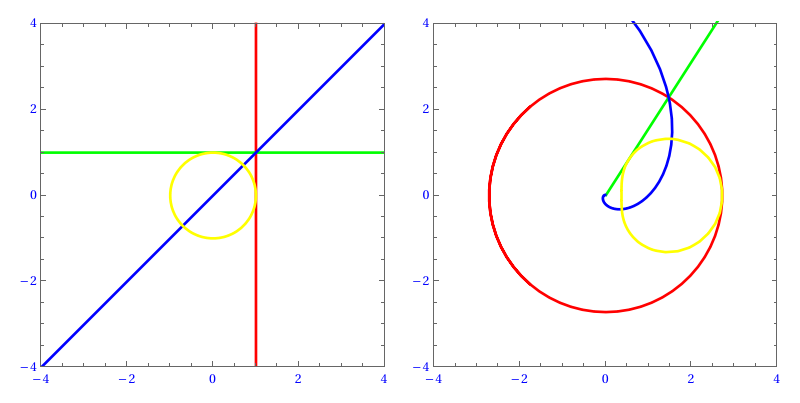
Original
expr = With[{z = x + I*y}, E^z // ReIm // ComplexExpand] xy = ParametricPlot[{x, y}, {x, -2, 2}, {y, -2, 2}, MeshFunctions -> {#1 &, #2 &, #2 - #1 &, Sqrt[#1^2 + #2^2] &}, Mesh -> {{1}, {1}, {0}, {1}}, MeshStyle -> {{Thick, Red, Opacity[1]}, {Thick, Green, Opacity[1]}, {Thick, Blue, Opacity[1]}, {Thick, Yellow, Opacity[1]}}, PlotPoints -> 50, FrameLabel -> {x, y}, PlotStyle -> None]; uv = ParametricPlot[expr, {x, -4, 4}, {y, -4, 4}, MeshFunctions -> {#3 &, #4 &, #4 - #3 &, Sqrt[#3^2 + #4^2] &}, Mesh -> {{1}, {1}, {0}, {1}}, MeshStyle -> {{Thick, Red, Opacity[1]}, {Thick, Green, Opacity[1]}, {Thick, Blue, Opacity[1]}, {Thick, Yellow, Opacity[1]}}, Axes -> False, PlotRange -> 8, BoundaryStyle -> None, FrameLabel -> {u, v}, LabelStyle -> {FontFamily -> "Times", Blue}, PlotPoints -> 80, PlotStyle -> None]; GraphicsRow[{xy, uv}] 