2
$\begingroup$

I plot two square lattices where one of them is rotated by 30 degrees. The Mathematica command to generate them is

{GridGraph[{5, 5}], Rotate[GridGraph[{5, 5}], 30]}

but I wonder whether it is possible to plot them right on top of each other to generate a Moire grid?

see here for instance

Improve this question
$\endgroup$
2
  • $\begingroup$ @Syed you are a mathematica magician :) thanks $\endgroup$ Commented Aug 13, 2021 at 15:03
  • $\begingroup$ Overlay[{GridGraph[{5, 5}], Rotate[GridGraph[{5, 5}], 45 Degree]}, Alignment -> Center] I forgot to write Degree, so deleted the previous comment. $\endgroup$ Commented Aug 13, 2021 at 17:54

1 Answer 1

Reset to default
2
$\begingroup$ 
g1 = GridGraph[{5, 5}]

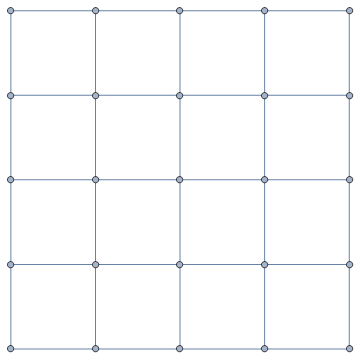
enter image description here

We can use RotationTransform and GraphEmbedding to rotate the vertex coordinates of the input graph:

ClearAll[rotateVCoords] rotateVCoords[angle_: 30 Degree] := RotationTransform[angle, Mean @ #] @ # &[GraphEmbedding @ #] & SetProperty[g1, VertexCoordinates -> rotateVCoords[][g1]]

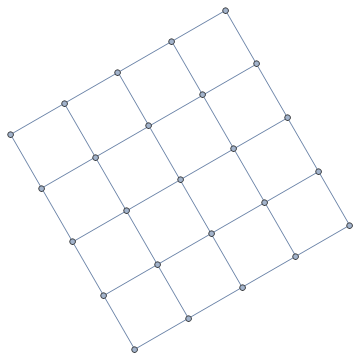
enter image description here

frames = Show[g1, SetProperty[g1, VertexCoordinates -> rotateVCoords[# Degree][g1]], PlotRange -> MinMax /@ Transpose[rotateVCoords[45 Degree][g1]], PlotRangePadding -> Scaled[.05]] & /@ Range[0, 360, 3]; Export["rotatevcoords.gif", frames, AnimationRepetitions -> ∞]

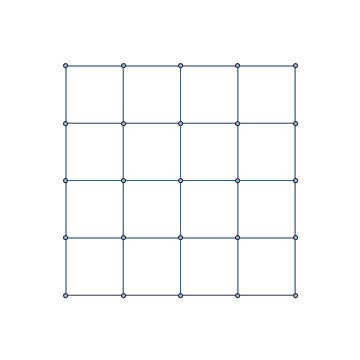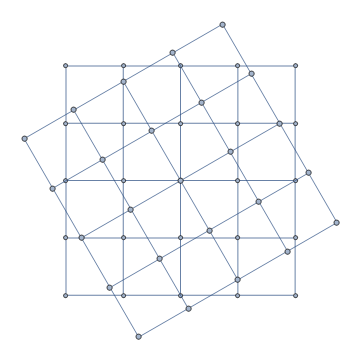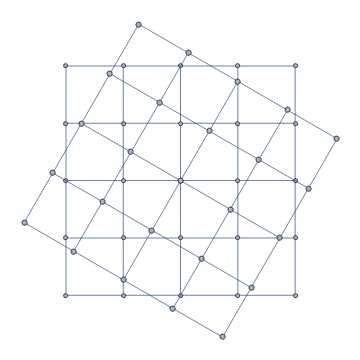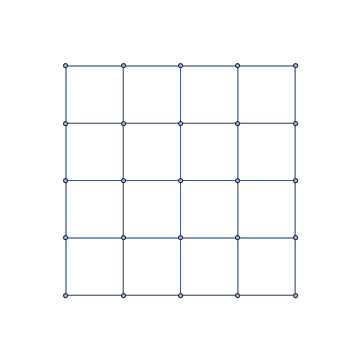
enter image description here

We can use rotateVCoords in two ways: (1) With Show + SetProperty to get a Graphics object, (2) With GraphUnion + IndexGraph to get a Graph object as output:

ClearAll[rotateAndCombineToGraphics, rotateAndCombineToGraph] rotateAndCombineToGraphics[angle_: 30 Degree] := Show[#, SetProperty[#, VertexCoordinates -> rotateVCoords[angle][#]]] & rotateAndCombineToGraph[angle_: 30 Degree] := GraphUnion[#, IndexGraph[#, 1 + VertexCount @ #], VertexCoordinates -> Join[GraphEmbedding @ #, rotateVCoords[angle][#]], ##2] &

Examples:

rotateAndCombineToGraphics[] @ g1

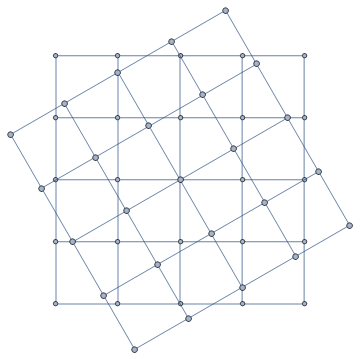
enter image description here

Head @ % 
Graphics 
rotateAndCombineToGraph[] @ g1

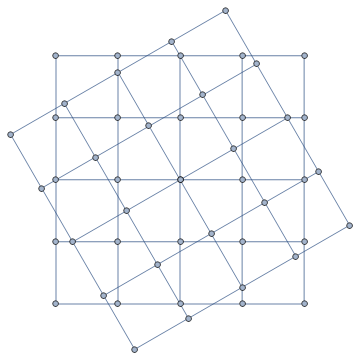
enter image description here

Head @ % 
Graph

With the second approach, we can add Graph options:

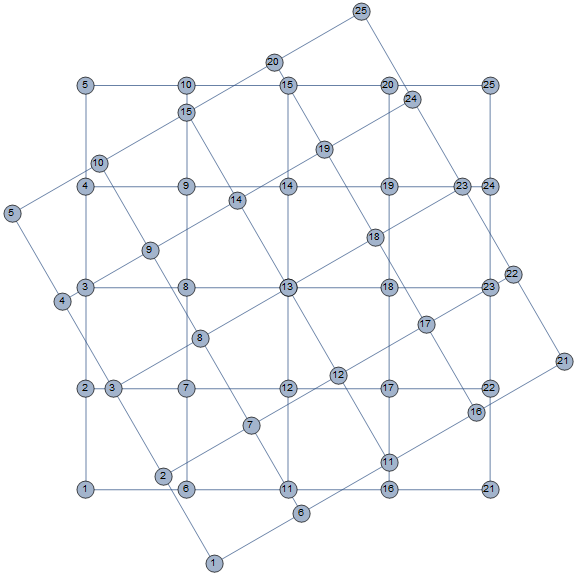
rotateAndCombineToGraph[][g1, ImageSize -> Large, VertexSize -> Scaled[.03], VertexLabels -> {v_ :> Placed[Mod[v, VertexCount[g1], 1], Center]}]

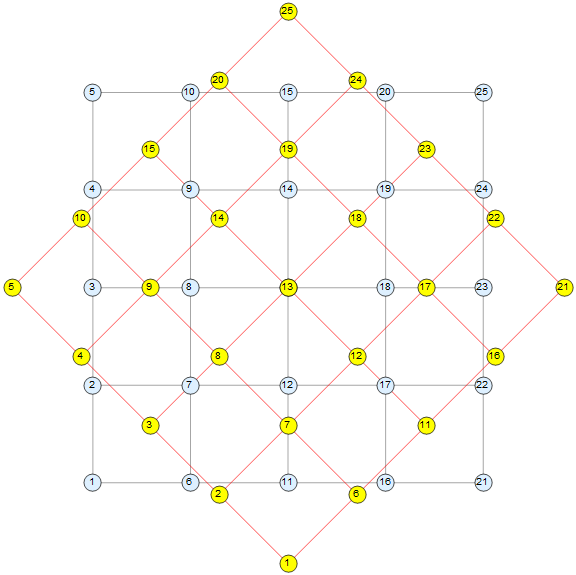
enter image description here

rotateAndCombineToGraph[45 Degree][g1, ImageSize -> Large, VertexSize -> Scaled[.03], VertexLabels -> {v_ :> Placed[Mod[v, VertexCount[g1], 1], Center]}, VertexStyle -> {v_ :> If[v > VertexCount[g1], Yellow, LightBlue]}, EdgeStyle -> {_ :> Red, Alternatives @@ EdgeList[g1] :> Gray}]

enter image description here

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.