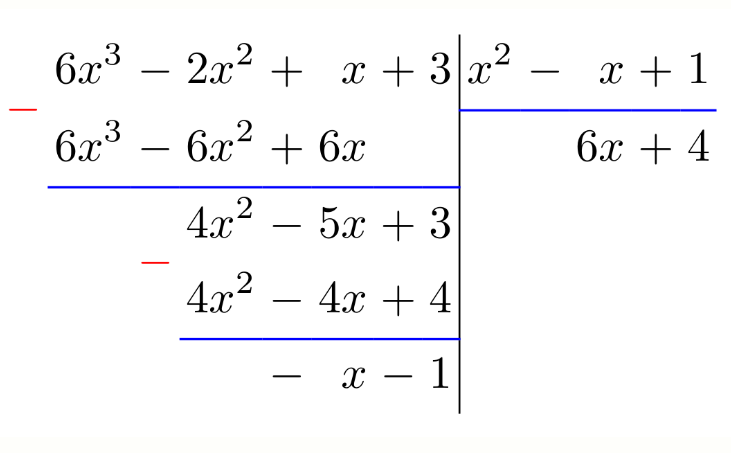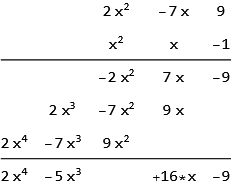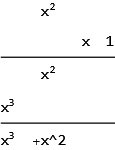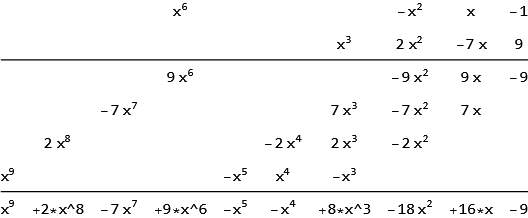In Latex, you could use how-can-i-make-a-scheme-to-multiply-polynomials but that answer only uses the coefficients. i.e. there will be no $x$ displayed in the process as you can see and one have to know the degree of $x$ by its position by inspection.
In Mathematica, here is a quick hack. But conversion this to Latex will need extra credit ;) and I am not sure now how much more effort it will take. The result is in a Grid.
mulp[x^2+x-1,2x^2-7x+9,x]
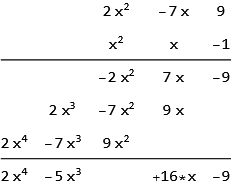
mulp[1+x,x^2,x]
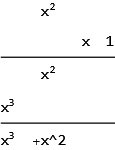
mulp[x^6-x^2+x-1,2x^2-7x+x^3+9,x]
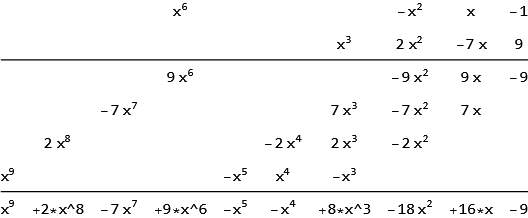
Code
ClearAll["Global`*"]; ClearAll[mulp] (*version June 23, 2023. Bug reports are welcome*) mulp[p1_,p2_,x_Symbol]:=Module[{max,min,cmin,cmax,g,n,m,pmin,pmax,tmp,w,currentRow,e,sum,currentCol,gridLines}, If[Not[PolynomialQ[p1,x]]||Not[PolynomialQ[p2,x]],Abort[]]; If[Length[CoefficientList[p1,x]]<=Length[CoefficientList[p2,x]], pmin=p1;pmax=p2 , pmin=p2;pmax=p1 ]; cmin=CoefficientList[pmin,x]; cmax=CoefficientList[pmax,x]; w=Length@cmax+Length@cmin-1; g=Table[0,{n,2+Length[cmin]+1},{m,w}]; Do[g[[1,w-n+1]]=cmax[[n]]*x^(n-1),{n,1,Length[cmax]}]; Do[g[[2,w-n+1]]=cmin[[n]]*x^(n-1),{n,1,Length[cmin]}]; Do[ currentRow=2+n; e=g[[2,w-n+1]]; Do[ currentCol=w-m+1-n+1; g[[currentRow,currentCol]]=e*g[[1,w-m+1]], {m,1,Length[cmax]}], {n,1,Length[cmin]} ]; currentRow=Length@g; Do[ e=Total[g[[3;;,n]]]; g[[currentRow,n]]=If[n>1,If[Internal`SyntacticNegativeQ[e]||e===0,e,"+"<>ToString[InputForm@e]],e] , {n,1,w} ]; gridLines=Table[If[n==3||n==Length[g],True,False],{n,Length@g}]; Grid[Replace[g,0->"",{2}],Spacings->{1, 1},Dividers->{{False},gridLines}] ]