46
$\begingroup$

I just saw a nice plot there:

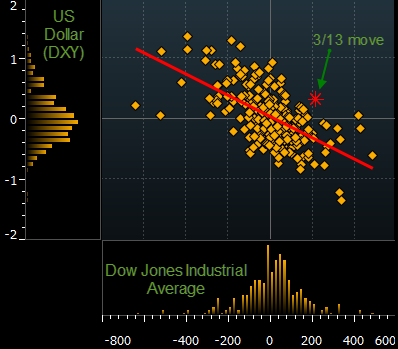
enter image description here

How could I implement that in Mathematica — by which I mean the plot structure, not so much the styling.

Improve this question
$\endgroup$
4
  • 3
    $\begingroup$ That's not fair, Mike, I have to get a lot of work done today. :) $\endgroup$ Commented Mar 14, 2012 at 21:32
  • 2
    $\begingroup$ We should both wait for Heike to make something very nice. :) $\endgroup$ Commented Mar 14, 2012 at 21:34
  • $\begingroup$ @Verbeia you'll recognize the plot as being from Bloomberg. They also have a plot style for line plots with a gradient fill below the line. Has anyone ever implemented that in Mma? I was thinking of posting that as a question. $\endgroup$ Commented Mar 14, 2012 at 21:43
  • $\begingroup$ Look at my answer: yes, I did recognise it as being from Bloomberg :D. I haven't tried to create a gradient Filling before - it's not the sort of thing we do at my employer. We are quite minimalist on the decoration side. $\endgroup$ Commented Mar 14, 2012 at 21:47

4 Answers 4

Reset to default
48
$\begingroup$

Here's my solution, which constructs the three components and uses Inset to combine them into a single graphic. I've taken some care so that:

  • the coordinate systems should line up across the plots (check the gridlines)
  • as many graphics and plotting options are respected without breaking the layout
  • the graphic can be reasonable resized
customPlot[data_, o___] := Block[{xmin, xmax, ymin, ymax, x, y, mainplot, xhist, yhist, opts = Flatten[{o}]}, {x, y} = Transpose[data]; xhist = HistogramList[x, 50]; yhist = HistogramList[y, 50]; {xmin, xmax} = Through[{Min, Max}[First[xhist]]]; {ymin, ymax} = Through[{Min, Max}[First[yhist]]]; mainplot = ListPlot[data, Frame -> {{False, True}, {False, True}}, Axes -> False, FrameTicks -> None, AspectRatio -> 1, PlotRange -> {{xmin, xmax}, {ymin, ymax}}, PlotRangePadding -> Scaled[0.02], ImagePadding -> {{None, 1}, {None, 1}}, FilterRules[opts, Options[ListPlot]], FrameStyle -> GrayLevel[0.3], GridLines -> Automatic, GridLinesStyle -> Directive[Gray, Dotted]]; xhist = Histogram[x, {First[xhist]}, Frame -> {{True, True}, {True, False}}, FrameTicks -> {{None, None}, {Automatic, None}}, Axes -> False, AspectRatio -> 1/3, ImagePadding -> {{1, 1}, {None, All}}, FilterRules[opts, Options[Histogram]], GridLines -> {Automatic, None}, FrameStyle -> GrayLevel[0.3], GridLinesStyle -> Directive[Gray, Dotted]]; yhist = Histogram[y, {First[yhist]}, Frame -> {{True, False}, {True, True}}, Axes -> False, FrameTicks -> {{Automatic, None}, {None, None}}, AspectRatio -> 3, BarOrigin -> Left, ImagePadding -> {{All, None}, {1, 1}}, FilterRules[opts, Options[Histogram]], GridLines -> {None, Automatic}, FrameStyle -> GrayLevel[0.3], GridLinesStyle -> Directive[Gray, Dotted]]; Graphics[{{Opacity[0], Point[{{360, 360}, {-120, -120}}]}, Inset[mainplot, {0, 0}, {Left, Bottom}, {360, 360}], Inset[xhist, {0, 0}, {Left, Top}, {360, Automatic}], Inset[yhist, {0, 0}, {Right, Bottom}, {Automatic, 360}]}, PlotRange -> {{-120, 360}, {-120, 360}}, FilterRules[opts, Options[Graphics]], ImagePadding -> {{30, 1}, {30, 1}}] ]

Now to create some data and try it out:

d = RandomVariate[BinormalDistribution[{0, 0}, {1, 2}, 0.4], 100]; customPlot[d]

enter image description here

customPlot[d, PlotStyle -> Directive[PointSize[Large], Orange], ChartStyle -> Orange, ChartElementFunction -> "FadingRectangle", FrameStyle -> White, Background -> Black]

enter image description here

Improve this answer
$\endgroup$
4
  • $\begingroup$ nice one Brett. :) $\endgroup$ Commented Mar 15, 2012 at 0:58
  • 2
    $\begingroup$ This can occasionally get misaligned due to the placement of the plot markers. Try evaluating it many times and you'll get a random dataset that shows this eventually. Here's an example I got by accident: i.sstatic.net/M7ulr.png I really really wish it were easier and less painful to robustly align things in Mathematica ... $\endgroup$ Commented Mar 15, 2012 at 8:33
  • 2
    $\begingroup$ @Szabolcs I just set ImagePadding on all the components to fix this (which means that tick labels may get clipped slightly.) $\endgroup$ Commented Mar 15, 2012 at 14:29
  • 1
    $\begingroup$ @BrettChampion Very pretty ;-) $\endgroup$ Commented Mar 16, 2012 at 6:06
49
$\begingroup$

There is also a more eye-catchy approach that uses built-in functions.

data = RandomReal[BinormalDistribution[{-1, 2}, {1, 1}, .8], 1000]; GraphicsColumn[ Table[DensityHistogram[data, {.2}, ColorFunction -> "DarkRainbow", Method -> {"DistributionAxes" -> p}, ImageSize -> 500, BaseStyle -> {FontFamily -> "Helvetica"}, LabelStyle -> Bold], {p, {True, "Histogram", "SmoothHistogram", "BoxWhisker"}}]]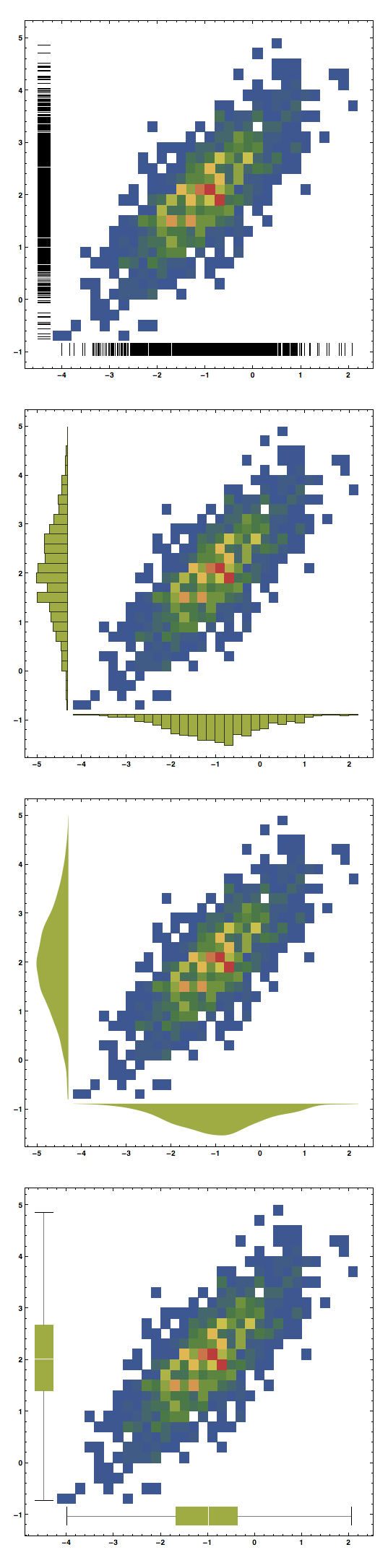

densitiy histograms

And it works also with SmoothDensityHistogram, although it seems that in this case Histogram cannot be used as a method:

GraphicsColumn[ Table[SmoothDensityHistogram[data, ColorFunction -> "DarkRainbow", Method -> {"DistributionAxes" -> p}, ImageSize -> 500, BaseStyle -> {FontFamily -> "Helvetica"}, LabelStyle -> Bold], {p, {True, "SmoothHistogram", "BoxWhisker"}}]]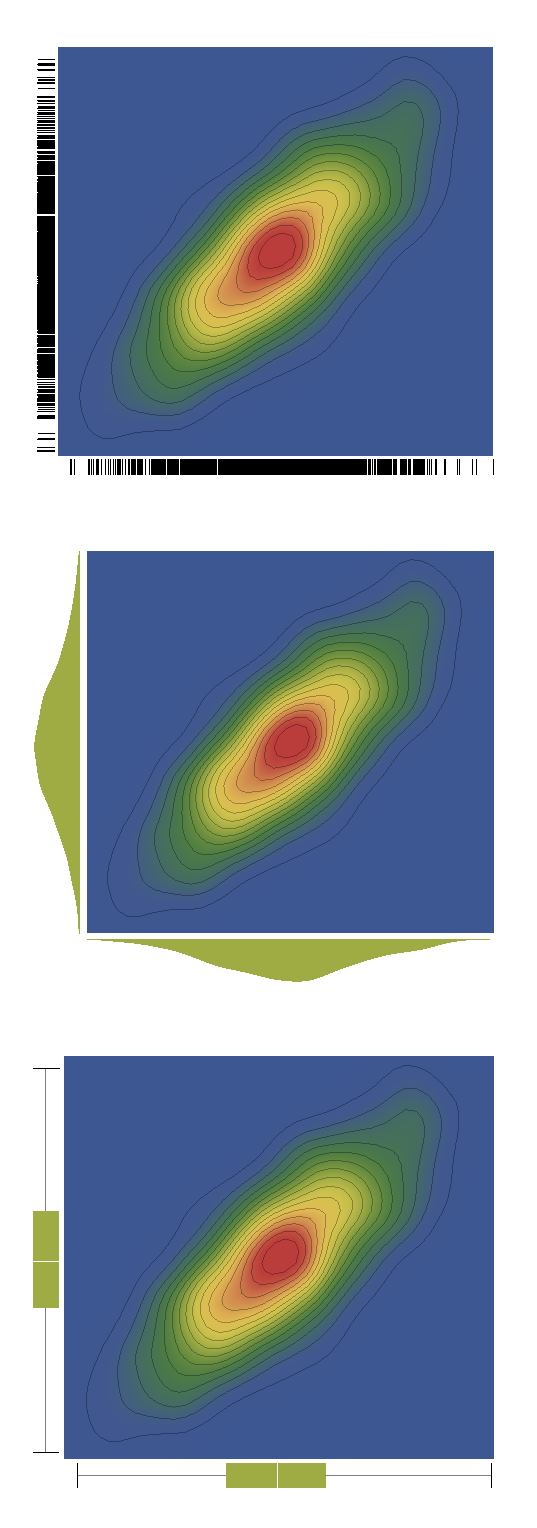

enter image description here

Scatterplot with histograms

data = RandomReal[BinormalDistribution[{0, 0}, {1, 1}, .8], 1000]; hist = DensityHistogram[data, {.2}, Method -> {"DistributionAxes" -> "Histogram"}][[1, 2]]; Show[ Graphics[hist, AspectRatio -> 1, Frame -> True, PlotRangeClipping -> True, PlotRangePadding -> {{Scaled[0.02], Scaled[0.02]}, {Scaled[0.02], Scaled[0.02]}}], ListPlot[data] ]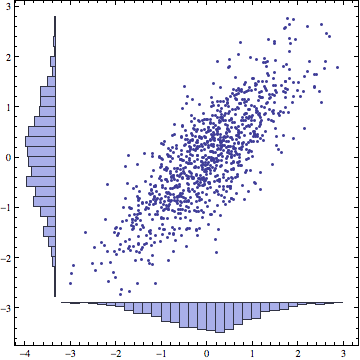

enter image description here

Improve this answer
$\endgroup$
10
  • 2
    $\begingroup$ Where did you learn about all the options for Method -> {"DistributionAxes" ->...} only "BoxWhisker" is listed in the examples. $\endgroup$ Commented Mar 30, 2012 at 6:18
  • 3
    $\begingroup$ I stumbled upon an example that used the Histogram as a "DistributionAxes" option, so I followed then the trial-and-error method to find other solutions. It might well be that there are other options out there that work. $\endgroup$ Commented Mar 30, 2012 at 6:38
  • 15
    $\begingroup$ Disappointing when users have to guess at these things. they should be documented. $\endgroup$ Commented Mar 30, 2012 at 7:18
  • 5
    $\begingroup$ @Brett I think all material relevant to a function should be documented at the function page (novel concept??). That is where people look. i.e. if a user wants information about a function should they go to the function page or scroll through the whats new in version 8 page? Seriously! [ShakngHeadSmiley] $\endgroup$ Commented Mar 31, 2012 at 21:35
  • 1
    $\begingroup$ I was just going through Edward Tufte's book - "A Visual Display of Quantitative Information" and saw this (or something very similar to the first "True" example) applied to a scatter plot... Is there no built-in functionality in ListPlot for this? Is the easiest way to overlay the scatter plot on the parts pulled from the histogram? $\endgroup$ Commented Oct 23, 2012 at 20:22
19
$\begingroup$

This doesn't have the styling and it doesn't yet enforce the plot ranges or implement the regression line, but it's a start:

fakeBloombergThing[data:{{_?NumericQ, _?NumericQ}..}] := Grid[{{Histogram[data[[All, 2]], BarOrigin -> Left , AspectRatio -> 5, ImageSize -> 80], ListPlot[data, Frame -> True, AspectRatio -> 1, ImageSize -> 350]}, {Null, Histogram[data[[All, 1]] , AspectRatio -> 1/5, ImageSize -> 350]}}]

Some fake data:

testdata = RandomVariate[BinormalDistribution[{-1, 1}, {1, 2}, -.6], 100]; fakeBloombergThing[testdata]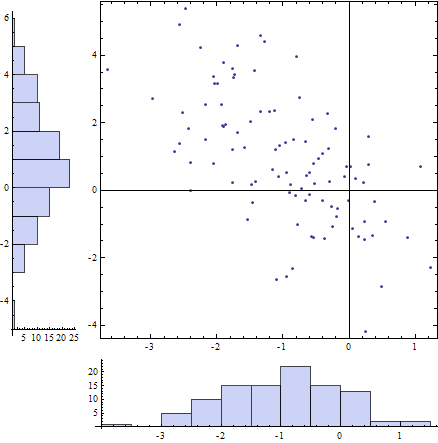

enter image description here

Improve this answer
$\endgroup$
2
  • $\begingroup$ I'd probably add some fixed ImagePadding as well for cases where significant figures in ticks can be large. That might also correct the misalignment of the "Y" histogram x axis with the scatter plot x axis. $\endgroup$ Commented Mar 14, 2012 at 21:58
  • $\begingroup$ Yes, I hadn't finessed that stuff yet. People should feel free to edit this. $\endgroup$ Commented Mar 14, 2012 at 22:00
19
$\begingroup$

Here's a truly hacky approach that uses Show to align a ListPlot of the points with the DensityHistogram, which we use only for the histograms along the axes. In order to hide the actual density histogram, we make everything white (which somewhat limits the styling options).

somePoints = RandomReal[BinormalDistribution[{-1, 2}, {1, 1}, .8], 1000]; Show[ DensityHistogram[somePoints, {.2}, ColorFunction -> (White &), Method -> {"DistributionAxes" -> "Histogram"}], ListPlot[somePoints]]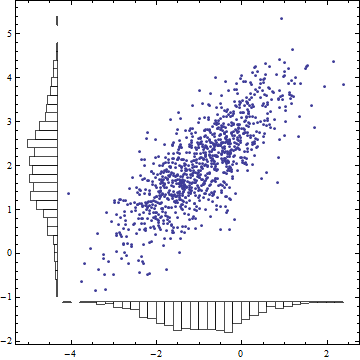

the plot

Improve this answer
$\endgroup$
1
  • 2
    $\begingroup$ You can have more flexibility using ColorFunction -> (Opacity[0] &) instead of ColorFunction->(White &) $\endgroup$ Commented Mar 30, 2012 at 3:54

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.