3
$\begingroup$

here is the code I am using - having issues getting started in FEA for this simple beam model. The problem is simple - I have looked at posted examples of MMA FEA, but they are all 2D and 3D problems. If I can get this simple 1D model made and play with it, I know I can get a better understanding of the general approach for MMA FEA.

(*Define parameters*) Ls = 10; (*Length of the beam in meters*) Es = 210*10^9; (*Young's modulus in Pascals*) Is = 1*10^-6; (*Moment of inertia in m^4*) qs = 1000; (*Uniform load in N/m applied over half the beam*) (*Load function definition*) loadFunction[x_] := If[x <= Ls/2, qs, 0]; (*Beam equation setup using FEM*) Needs["NDSolve`FEM`"]; (*ToElementMesh["Coordinates"\[Rule]{{0},{Ls}},"MeshElements"\[Rule]{\ LineElement[{{1,2}}]}] beamDomain=ToElementMesh[LineElement[{0,0},{0,Ls}]];*) beamDomain = ToElementMesh[Line[{0, 0}, {0, Ls}]]; (*Check if mesh is created properly*) MeshRegion[beamDomain] (*Boundary conditions for a simply supported beam*) boundaryConditions = {w[0] == 0, w[Ls] == 0, Derivative[2][w][0] == 0, Derivative[2][w][Ls] == 0}; (*Beam equation*) beamPDE = Es*Is*D[w[x], {x, 4}] + loadFunction[x] == 0; (*Solve the beam equation using NDSolve with FEM*) solution = NDSolveValue[{beamPDE, boundaryConditions}, w, {x, 0, Ls}, Method -> {"FiniteElement"}]; (*Plot the deflection diagram*) Plot[solution[x], {x, 0, Ls}, PlotLabel -> "Deflection Diagram", AxesLabel -> {"x (m)", "w(x) (m)"}] (*Calculate shear force V(x)=-EI*d^3w/dx^3*) shearForce = -Es*Is*D[solution[x], {x, 3}]; (*Plot the shear force diagram*) Plot[shearForce, {x, 0, Ls}, PlotLabel -> "Shear Force Diagram", AxesLabel -> {"x (m)", "V(x) (N)"}] (*Calculate bending moment M(x)=-EI*d^2w/dx^2*) bendingMoment = -Es*Is*D[solution[x], {x, 2}]; (*Plot the bending moment diagram*) Plot[bendingMoment, {x, 0, Ls}, PlotLabel -> "Bending Moment Diagram", AxesLabel -> {"x (m)", "M(x) (N*m)"}]
Improve this question
$\endgroup$
3
  • 1
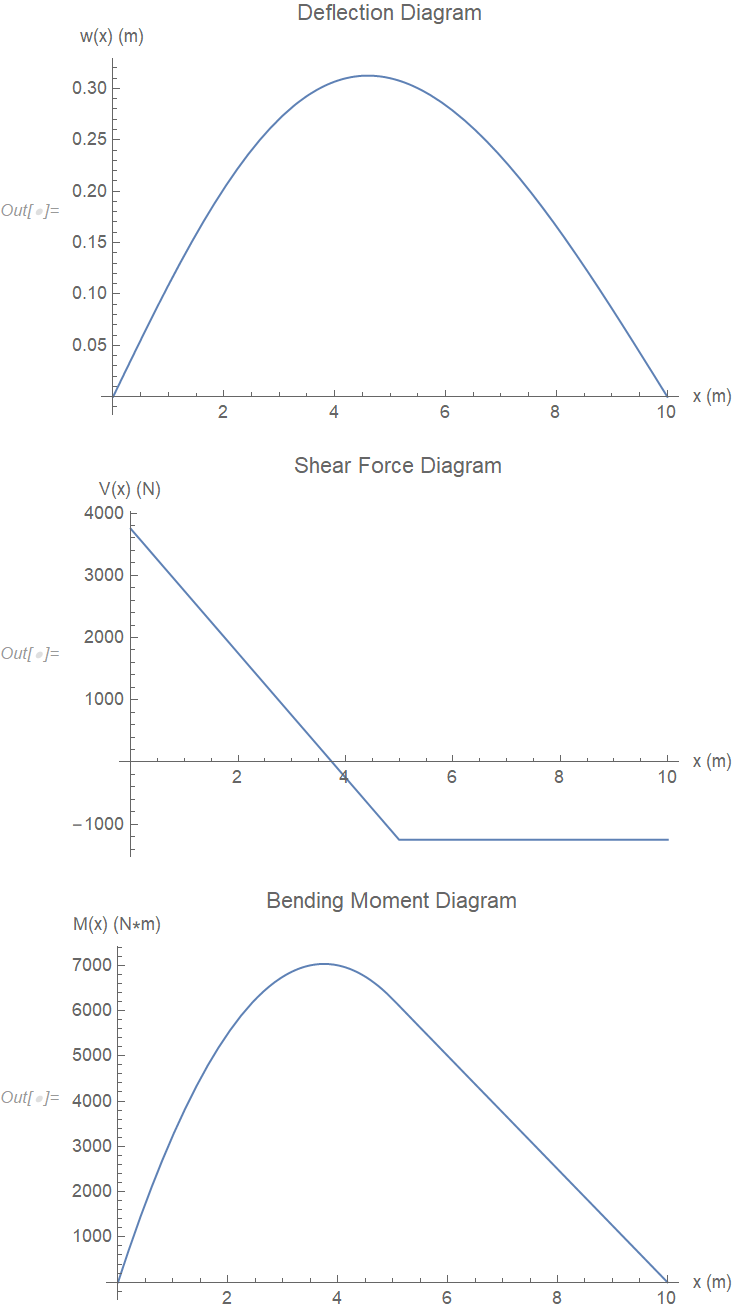
    $\begingroup$ You don’t need FEM to solve this ODE. This works for me: solution = NDSolveValue[{beamPDE, boundaryConditions}, w, {x, 0, Ls}] and then the plots work fine. $\endgroup$ Commented May 27, 2024 at 23:33
  • 1
    $\begingroup$ Have you read e.g. mathematica.stackexchange.com/q/224812/1871 and mathematica.stackexchange.com/a/199369/1871 ? $\endgroup$ Commented May 28, 2024 at 3:34
  • $\begingroup$ Check your mesh definition. Better try beamDomain = ToElementMesh [ImplicitRegion[0 <= x <= Ls, x]]. You need to change your pde-system too, FEM only solves second order pde's in Mathematica $\endgroup$ Commented May 28, 2024 at 7:04

1 Answer 1

Reset to default
5
$\begingroup$

To make the FEM-solution work you have to change the element mesh and you have to transform the pde-system to second order.

From mechanical point of view you only have to define an additional unknown moment[x] == -Es*Is*D[w[x], {x, 2}]

(*Define parameters*)Ls = 10;(*Length of the beam in meters*)Es = 210*10^9;(*Young's modulus in Pascals*)Is = 1*10^-6;(*Moment of inertia in m^4*)qs = 1000;(*Uniform load in N/m \ applied over half the beam*)(*Load function definition*) loadFunction[x_] := If[x <= Ls/2, qs, 0]; (*Beam equation setup using FEM*) Needs["NDSolve`FEM`"]; beamDomain = ToElementMesh [ImplicitRegion[0 <= x <= Ls, x]] ; (*Boundary conditions for a simply supported beam*) boundaryConditions = {w[0] == 0, w[Ls] == 0, moment[0] == 0, moment[Ls] == 0}; (*Beam equation*) beamPDE = { D[moment[x], {x, 2}] + loadFunction[x] == 0, moment[x] == -Es*Is*D[w[x], {x, 2}]}; (*Solve the beam equation using NDSolve with FEM*) solution = NDSolveValue[{beamPDE, boundaryConditions}, {w, moment}, {x, 0, Ls}, Method -> {"FiniteElement"}] ; (*Plot the deflection diagram*) Plot[solution[[1]][x], {x, 0, Ls}, PlotLabel -> "Deflection Diagram", AxesLabel -> {"x (m)", "w(x) (m)"}] (*Calculate shear force V(x)=-EI*d^3w/dx^3*) shearForce = -Es*Is*D[solution[x], {x, 3}]; (*Plot the shear force diagram*) Plot[solution[[2]]'[x], {x, 0, Ls}, PlotLabel -> "Shear Force Diagram", AxesLabel -> {"x (m)", "V(x) (N)"}] (*Plot the bending moment diagram*) Plot[solution[[2]][x], {x, 0, Ls}, PlotLabel -> "Bending Moment Diagram", AxesLabel -> {"x (m)", "M(x) (N*m)"}]

enter image description here

Hope it helps!

Improve this answer
$\endgroup$
8
  • $\begingroup$ One last issue - Hoe can I add an additional BC at some point along the beam. Example - like adding at L2/2 a pin connection. When I try to add a BC like that, I get an error message - NDSolveValue::bcnop: No places were found on the boundary where x==30. was True, so DirichletCondition[w==0,x==30.] will effectively be ignored. Tried Coordinates" -> meshPoints, MeshRefinementFunction, but nothing appears to put a point on the mesh that I can define as another BC ( ie from 2 support points on the beam to 3 support points on the beam) $\endgroup$ Commented May 28, 2024 at 19:55
  • $\begingroup$ @SAK L2 isn't defined, perhaps you mean LS? Please show your additional bc! $\endgroup$ Commented May 29, 2024 at 9:52
  • $\begingroup$ boundaryConditions = { w[0] == 0,(* Displacement @1 st beam - pin left end ) momentw[0] == 0,( moment @1 st beam - pin left end ) w[Lspan] == 0, ( Displacement@ 1 st beam - pin right end ) v[Lspan] == 0, ( Displacement @ 2 nd beam - pin left end ) v'[Lspan] + w'[Lspan] == 0, ( slope continuity between beam 1 + beam 2 at joint ) v[Ls] == 0,( Displacement @2 nd beam - pin right end ) momentw[Lspan] + momentv[Lspan] == 0, ( moment equalibrum between beam 1@ beam 2 joint ) momentv[Ls] == 0 ( moment @ 2 nd beam - pin right end *) } $\endgroup$ Commented May 29, 2024 at 22:06
  • $\begingroup$ @SAK Your last comment is a little bit confusing, "two beams, unknown paramater Lspan,..." . To make an inner point a boundary try option "IncludePoints" ToElementMesh[...,"IncludePoints"->{{Ls/2,0}}] $\endgroup$ Commented May 30, 2024 at 7:46
  • $\begingroup$ the code does run - with added points - BUT the answer is wrong as the deflection at Ls/2 should be zero and it is not. additionalPoints = {{Ls/2}} beamDomain = ToElementMesh[ImplicitRegion[0 <= x <= Ls, x], "IncludePoints" -> additionalPoints]["Wireframe"] boundaryConditions = {w[0] == 0,(w[Ls/2]==0,)w[Ls] == 0, moment[0] == 0,(moment[Ls/2]==0,)moment[Ls] == 0}; solution = NDSolveValue[{beamPDE, boundaryConditions, DirichletCondition[{w[Ls/2] == 0, moment[Ls/2] == 0}, True]}, {w, moment}, {x, 0, Ls}, Method -> {"FiniteElement"}]; $\endgroup$ Commented May 30, 2024 at 20:34

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.