1
$\begingroup$

I'm trying to integrate the following expression:

f[a1,p1+p2+p3+p4]*f[a2,p2+p3+p4]*f[a3,p3+p4]*f[a4,p4]

Where

f[x_, u_] := E^(-(x - u)/2)/(2*(1 + E^(-(x - u)/2))^2)

i.e. the PDF of the logistic distribution with s=2.

Also, the a's are positive integers.

The tricky part is that I want to integrate over all values of the p values that result in them forming a valid probability distribution, ie the p variables must be greater than zero, less than one and sum to 1.

I've tried using a definite integral with the following limits (after substituting p4 with $1-p1-p2-p3$:

{p1,0,1},{p2,0,1-p1},{p3,0,1-p2-p3}

This works for a simplified version of the problem (with 3 or 2 "f" terms and p variables but as soon as I use 4 it takes about 20 minutes and then just returns the input. My instinct is that if it can be analytically found for 3 terms, 4 terms should also be findable, just with more terms.

My question(s) are:

1) Does anyone have any suggestions to get Mathematica working for this (and larger problems)?

2) I'm not tied to the logistic distribution, I'm using it because I thought it's simple CDF would make the problem easy for Mathematica. Can anyone suggest a similar shaped distribution that would make this problem tractable?

Improve this question
$\endgroup$
7
  • $\begingroup$ I think these limits don't ensure $0 \leq p_i \leq 1$ and $\sum_{i} p_i =1$. $\endgroup$ Commented Jun 5, 2014 at 4:02
  • $\begingroup$ Are you sure? That's what I saw other people solving similar problems (eg this post $\endgroup$ Commented Jul 5, 2014 at 16:29
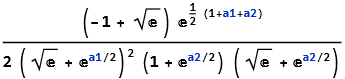
  • $\begingroup$ Is there some reason why you can't use NIntegrate ? I understand that a symbolic solution is desirable. But is a symbolic solution essential? $\endgroup$ Commented Nov 21, 2016 at 22:57
  • 1
    $\begingroup$ One can use Simplex[] instead: Integrate[expr, {p1, p2, p3} ∈ Simplex[{{0, 0, 0}, {1, 0, 0}, {0, 1, 0}, {0, 0, 1}}] $\endgroup$ Commented Mar 17, 2018 at 4:42
  • 1
    $\begingroup$ @Mahdi is right, you have a typo in your integration limits: the third one should be {p3, 0, 1-p1-p2}. $\endgroup$ Commented Apr 11, 2019 at 9:42

2 Answers 2

Reset to default
0
$\begingroup$

I think the problem is in limits you use because they don't ensure $0 \leq p_i \leq 1$ and $\sum_{i} p_i =1$. You have 4 $p_i$'s so you can only fix $p_4$. By using this relation, we can write the integrand as:

eq= f[a2, 1 - p1]*f[a3, 1 - p1 - p2]*f[a4, 1 - p1 - p2 - p3]*f[a1,1];

The last terms does not depend on $p_i$'s. Now you can easily find indefinite solution:

g=Integrate[eq,p1,p2,p3];

which is a function such that $g=g(p_1,p_2,p_3)$ with only one constraint $0 \leq p_1+p_2+p_3 \leq 1$. Then basically you can have value of $g$ over any valid combinations of $p_i$'s.

Improve this answer
$\endgroup$
2
  • $\begingroup$ So once I've done this and I have g, then I still need to integrate over p1,p2,p3 with the constraint that they're positive and are less than one? $\endgroup$ Commented Jul 5, 2014 at 16:33
  • 1
    $\begingroup$ I don't believe that the resulting indefinite integral recognizes the constraint $0 \leq p_1+p_2+p_3 \leq 1$. One can't just plug in 0 and 1 for the values of $p_1$, $p_2$, and $p_3$. Can you show that it does? $\endgroup$ Commented Nov 21, 2016 at 23:04
0
$\begingroup$

For $d=2$ (i.e., $p_1+p_2==1$), the resulting integration of f[a1, 1] f[a2, p2] is

Integral for d=2

But I'm not convinced there's a nice for closed-form for $d=3$ for general values of a2 and a3 (and the OP does not provide that closed-form). But numerical integration seems to work relatively fast:

f[x_, u_] := E^(-(x - u)/2)/(2*(1 + E^(-(x - u)/2))^2) g[aa_] := Module[{d, pp}, d = Length[aa]; pp = Array[p, d]; integrand = (d - 1)! f[aa[[1]], 1] Product[f[aa[[i]], Sum[p[j], {j, i, d}]], {i, 2, d}]; NIntegrate[integrand, {p[2], 0, 1}, Evaluate[Sequence @@ Table[{p[i], 0, p[i - 1]}, {i, 3, d}]]]]

For $d=4$, the execution time is

AbsoluteTiming[g[{1, 17, 2, 7}]] (* {0.0172144, 5.20969*10^-8} *)

For $d>4$ the execution time does increase dramically. If the OP would include the closed-form found for $d=3$, then that might help suggest what to do for $d>3$.

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.