7
$\begingroup$

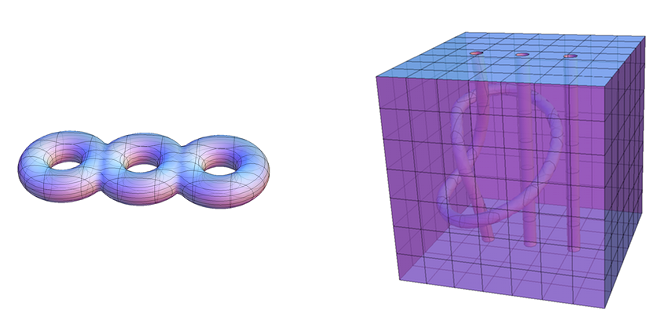
enter image description here

How to draw these two(especially the second one) graphs using Mathematica? The curve is not important.The point is how to dig some holes in a cube. BTW, These two shapes are Homotopy.

Improve this question
$\endgroup$
4
  • 1
    $\begingroup$ Providing functions for the figures or some example of what you have tried would be helpful. Start by looking at the documentation for ParametricPlot3D $\endgroup$ Commented Aug 1, 2014 at 2:05
  • $\begingroup$ Probable using RegionPlot3D $\endgroup$ Commented Aug 1, 2014 at 3:10
  • 2
    $\begingroup$ For the first surface, see How to draw a higher genus surface $\endgroup$ Commented Aug 1, 2014 at 3:33
  • 1
    $\begingroup$ Are these really homotopic? Homeomorphic, I can see - but homotopic requires a deformation that disentangles those tubes. Given an explicit homotopy, we should be able to animate the deformation. $\endgroup$ Commented Aug 1, 2014 at 13:19

2 Answers 2

Reset to default
11
$\begingroup$ 
r = 1/40; sides = ParametricPlot3D[{ {0, u, v}, {1, u, v}, {u, 1, v}, {u,0,v} }, {u, 0, 1}, {v, 0, 1}, Mesh -> 7, PlotStyle -> { Directive[Purple, Opacity[0.6]], Directive[Purple, Opacity[0.6]], Directive[Purple, Opacity[0.6]], Directive[Purple, Opacity[0.2]] }, MeshStyle -> { Directive[Opacity[0.2]], Directive[Opacity[0.2]], Directive[Opacity[0.2]], Directive[Opacity[0.05]] }, Boxed -> False, Axes -> False]; topBot = ParametricPlot3D[{ {u, v, 1}, {u, v, 0} }, {u, 0, 1}, {v, 0, 1}, Mesh -> 7, PlotStyle -> Directive[Purple, Opacity[.4]], MeshStyle -> Opacity[0.2], Boxed -> False, Axes -> False, PlotPoints -> 55, RegionFunction -> Function[{u, v}, (u - 1/5)^2 + (v - 1/2)^2 > r^2 && (u - 1/2)^2 + (v - 1/2)^2 > r^2 && (u - 4/5)^2 + (v - 1/2)^2 > r^2]]; p[t_] = {0.1 (Cos[4 Pi*t] - 2 Cos[2 Pi*t] + 1) + 1/5, 0.2 (Sin[4 Pi*t] - Sin[2 Pi*t]) + 1/2, ((2.5 (t - 1/2)) - (2.5 (t - 1/2))^3 + 45/64) 32/45}; tubes = ParametricPlot3D[{p[t], {1/2, 1/2, t}, {4/5, 1/2, t}}, {t, 0, 1}, PlotStyle -> Directive[Specularity[White,10], Purple, Opacity[.6]] ] /. Line[pts_] :> {CapForm[None], Tube[pts, r]}; join = ParametricPlot3D[{ {1/5, 1/2, 0} + r {Cos[t], Sin[t], 0}, {1/2, 1/2, 0} + r {Cos[t], Sin[t], 0}, {4/5, 1/2, 0} + r {Cos[t], Sin[t], 0}, {1/5, 1/2, 1} + r {Cos[t], Sin[t], 0}, {1/2, 1/2, 1} + r {Cos[t], Sin[t], 0}, {4/5, 1/2, 1} + r {Cos[t], Sin[t], 0} }, {t, 0, 2 Pi}, PlotStyle -> Directive[Thick, Purple, Opacity[0.2]] ]; Show[{sides, topBot, tubes, join}, ViewPoint -> {1.25833, -2.927, 1.1384}]

enter image description here

Improve this answer
$\endgroup$
6
  • 1
    $\begingroup$ where can I find the techniques like that /. Line[pts_] :> { , which is very cool because it is followed after the plot function and Line is not explicitly appear in the plot function. I just want to know more of these cool. $\endgroup$ Commented Aug 1, 2014 at 6:52
  • $\begingroup$ @MarkMcClure I could feel myself drilling the holes in the sides, bending the pipes, joining the ends to these sides then gluing the remaining 4 sides...very nice + 1 :) $\endgroup$ Commented Aug 1, 2014 at 7:10
  • 1
    $\begingroup$ @peter You can learn a lot about this type of programming in the documentation's section on the structure of graphics. In particular, you'll learn that plotting command (like ParametricPlot3D) produce graphics primitives (like Line). So, if you execute something like InputForm[ParametricPlot3D[{t,t,t}, {t,0,1}], you'll see that a Line has been produced. The /.Line[pts_] :> business simply replaces it with a Tube. $\endgroup$ Commented Aug 1, 2014 at 10:45
  • $\begingroup$ @MarkMcClure thank you very much.p[t_] = {0.1 (Cos[4 Pi*t] - 2 Cos[2 Pi*t] + 1) + 1/5, 0.2 (Sin[4 Pi*t] - Sin[2 Pi*t]) + 1/2, ((2.5 (t - 1/2)) - (2.5 (t - 1/2))^3 + 45/64) 32/45};can you tell me a little about how you came up with this function?is there some secret of making this... $\endgroup$ Commented Aug 5, 2014 at 3:31
  • $\begingroup$ @peter Honestly, I just looked at it. I figured the $z$ coordinate had to start way up high, go pretty low, then pretty high, then way down low - so I came up with $t-t^3$ over some interval. I then scaled and shifted that so that it fit. I did similar things with the $x$ and $y$ coordinates. Too much looking at functions over the years, I guess. $\endgroup$ Commented Aug 5, 2014 at 3:38
2
$\begingroup$

As MichaelE2's comment there are a number of ways of generating the left figure.

Using whubers circle function.:

circle[x_, n_: 32] := {x + Cos[#], Sin[#], 0} & /@ Range[0, 2 \[Pi], 2 \[Pi]/n]; Graphics3D[{LightBlue, Tube[circle[#] & /@ Range[-2, 2, 2], 0.4]}, Boxed -> False]

gives:

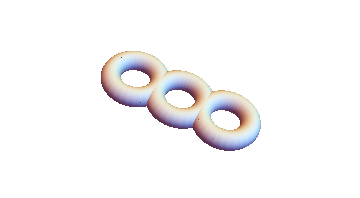
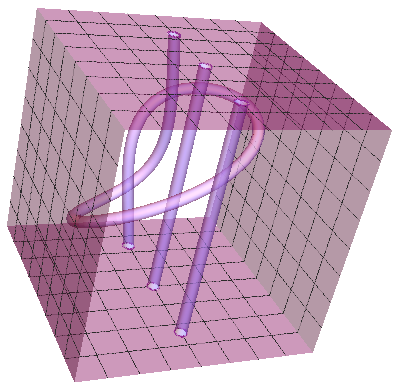
enter image description here

Mark McClure's construction of a boxes six sides, putting tubes inside and holes in parallel sides and joining the tube ends to the side holes gets my vote. Just looking inside the 'purple box' by removing two sides shows the internal plumbing:

enter image description here

I post the following (which "drills" holes in the cubic region), not as efficient but as a way, using Mark McClure's parametric curve. If the extrusion is too big the tube intersects itself and it takes much longer.

p[t_] = {0.1 (Cos[4 Pi*t] - 2 Cos[2 Pi*t] + 1) + 1/5, 0.2 (Sin[4 Pi*t] - Sin[2 Pi*t]) + 1/2, ((2.5 (t - 1/2)) - (2.5 (t - 1/2))^3 + 45/64) 32/45}; pp = ParametricPlot3D[p[t], {t, 0, 1}]; reg = First@Cases[pp, Line[x__], Infinity]; rf = RegionDistance[reg] h2 = Line[Table[{1/2, 1/2, j}, {j, 0, 1, 0.1}]]; rf2 = RegionDistance[h2]; h3 = Line[Table[{3/4, 1/2, j}, {j, 0, 1, 0.1}]]; rf3 = RegionDistance[h3]; RegionPlot3D[ rf[{x, y, z}] > 0.02 && rf2[{x, y, z}] > 0.02 && rf3[{x, y, z}] > 0.02, {x, 0, 1}, {y, 0, 1}, {z, 0, 1}, PlotStyle -> Opacity[0.5], Axes -> False, Boxed -> False, Mesh -> False, PlotPoints -> 100]

gives this:

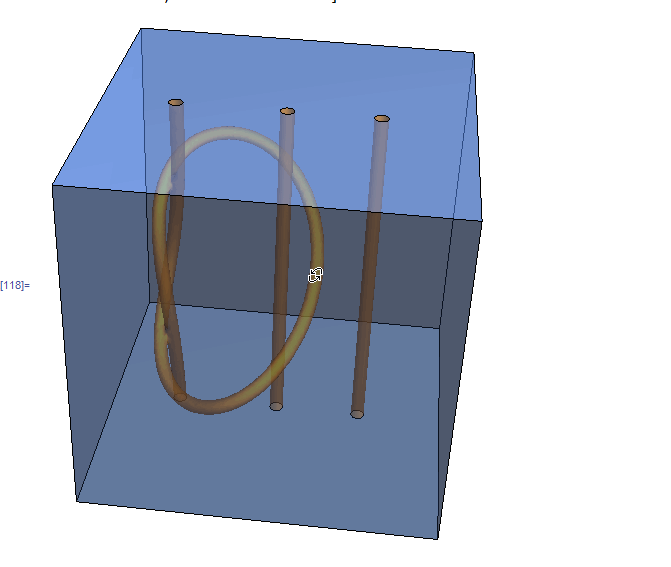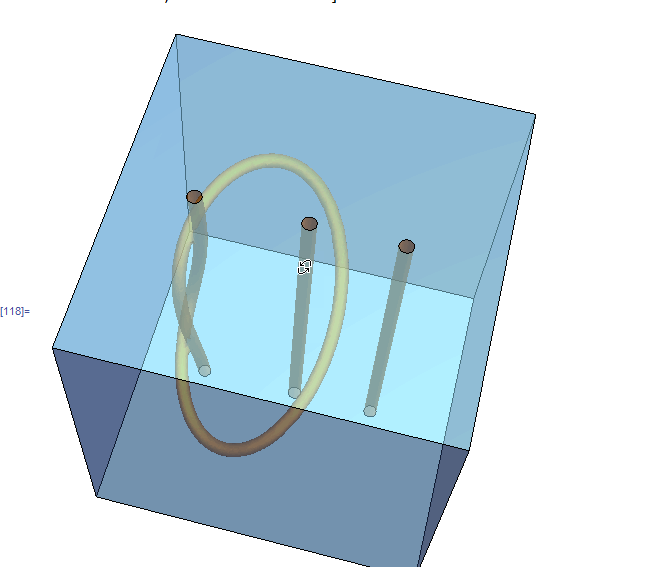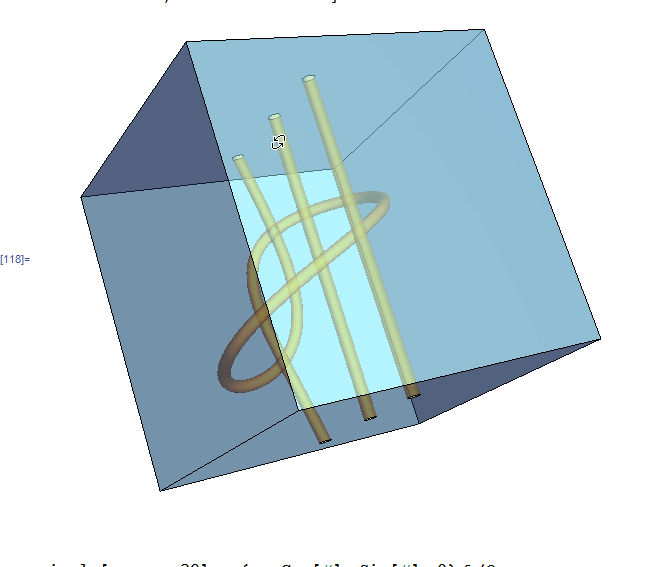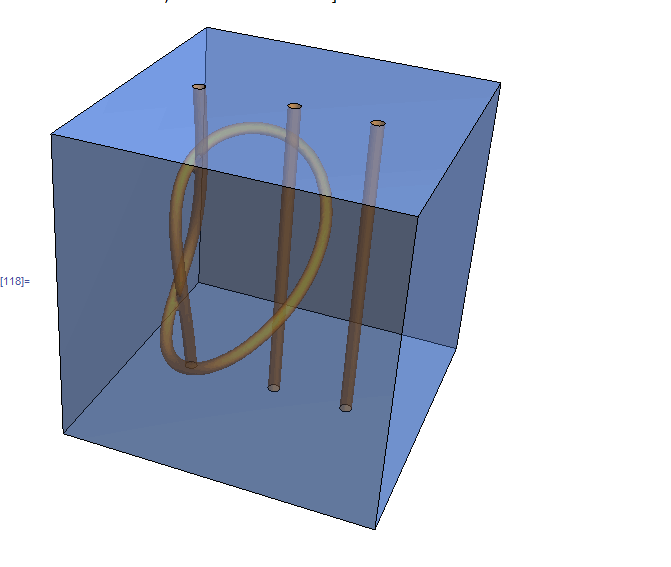
enter image description here

This takes sometime on my machine...

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.