18
$\begingroup$

Can Gaussian curvature $K$ be computed from WolframAlpha or any other available Mathematica program? Please indicate the program or its reference.

If input parametrization is given as Gaussian curvature of

X[u,v] = {Cos[u] Cos[v], Cos[u] Sin[v], Sin[u]}

it simply outputs an assembly of three individual Cartesian prismatic Monge 3D (u,v) plots and their plotted K but does not refer to meridians and parallels of a single unit sphere surface.

Improve this question
$\endgroup$
2

4 Answers 4

Reset to default
15
$\begingroup$

Note this parametric surface of unit sphere (S^2) should have constant Gaussian curvature: 1.

Surface:

x[u_, v_] := {Cos[u] Cos[v], Cos[u] Sin[v], Sin[u]}

First fundamental form:

fff = FullSimplify[With[{p1 = D[x[a, b], a], p2 = D[x[a, b], b]}, {p1.p1, p1.p2, p2.p2}]];

Second fundamental form:

nm = FullSimplify[Cross[D[x[a, b], a], D[x[a, b], b]]]; unm = FullSimplify[nm/Sqrt[nm.nm]]; sec = {D[x[a, b], {a, 2}], Derivative[1, 1][x][a, b], D[x[a, b], {b, 2}]}; sff = FullSimplify[#.unm & /@ sec];

Gaussian Curvature:

de[{e_, f_, g_}] = e g - f^2 FullSimplify[de[#1]/de[#2] & @@ {sff, fff}]

yields 1

The mean curvature:

FullSimplify[(sff Reverse[fff]).{1, -2, 1}/(2 de[fff])]

yields: Sqrt[Cos[a]^2] Sec[a], which is clearly 1 as required.

i.e. K=1, H=1, $\kappa1 =1,\kappa2=1$

Simplifications can be challenging...others will have better approaches

Improve this answer
$\endgroup$
6
  • $\begingroup$ Dear @ ubpdqn. Thanks for understanding Gauss. $\endgroup$ Commented Oct 6, 2014 at 8:20
  • $\begingroup$ @eldo "Die Mathematik ist die Königin der Wissenschaften..." $\endgroup$ Commented Oct 6, 2014 at 8:25
  • $\begingroup$ en.wikipedia.org/wiki/Sphere $\endgroup$ Commented Oct 6, 2014 at 8:30
  • 1
    $\begingroup$ @ubpdqn: Jawohl ...ihre Schönheit verdoppelt mit Mathematica. $\endgroup$ Commented Oct 6, 2014 at 9:35
  • $\begingroup$ @Narasimham I just posted the answer to illustrate a way to calculate Gaussian curvature for smooth surfaces (manifolds) using first and second fundamental forms. Varying x[u,v] should work for other surfaces, acknowledging issues of singular points, ugly expressions from limitations of simplifications. $\endgroup$ Commented Oct 6, 2014 at 9:44
32
$\begingroup$

Definition

GaussCurvature[f_] := With[{dfu = D[f, u], dfv = D[f, v]}, Simplify[(Det[{D[dfu, u], dfu, dfv}] Det[{D[dfv, v], dfu, dfv}] - Det[{D[f, u, v], dfu, dfv}]^2) / (dfu.dfu dfv.dfv - (dfu.dfv)^2)^2]];

Sphere

As @ ubpdqn already remarked

GaussCurvature[{Cos[u] Sin[v], Sin[u] Sin[v], Cos[v]}]

1

Ellipsoid

ellipsoid = {2 Cos[u] Sin[v], Sin[u] Sin[v], Cos[v]}; cur = GaussCurvature[ellipsoid]

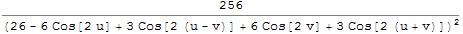
enter image description here

plo = Plot3D[cur, {u, 0, Pi}, {v, 0, 2 Pi}, ColorFunction -> "TemperatureMap", PlotRange -> Full]

enter image description here

range = Last[PlotRange /. AbsoluteOptions[plo, PlotRange]]

{0.25, 4.}

ParametricPlot3D[ellipsoid, {u, 0, Pi}, {v, 0, 2 Pi}, Mesh -> False, ColorFunction -> Function[{x, y, z, u, v}, ColorData["TemperatureMap"][Rescale[cur, range]]], ColorFunctionScaling -> False]

enter image description here

Torus

torus = {(2 + Cos[v]) Cos[u], (2 + Cos[v]) Sin[u], Sin[v]}; cur = GaussCurvature[torus]

enter image description here

plo = Plot3D[cur, {u, 0, 2 Pi}, {v, 0, 2 Pi}, ColorFunction -> "TemperatureMap", PlotRange -> Full]

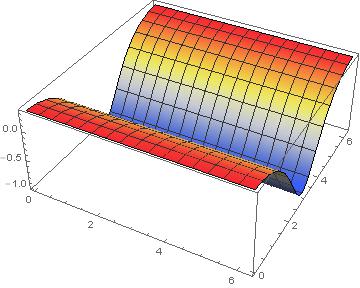
enter image description here

range = Last[PlotRange /. AbsoluteOptions[plo, PlotRange]]

{-1., 0.333333}

par = ParametricPlot3D[ torus, {u, 0, 2 Pi}, {v, 0, 2 Pi}, ImageSize -> 400, Mesh -> False, ColorFunction -> Function[{x, y, z, u, v}, ColorData["TemperatureMap"][Rescale[cur, range]]], ColorFunctionScaling -> False, PlotPoints -> 70]; bar = BarLegend[{"TemperatureMap", range}, Automatic]; Row[{par, bar}]

enter image description here

Moebius with gaussian mesh lines

f = {Cos[v] (3 + u Cos[v/2]), Sin[v] (3 + u Cos[v/2]), u Sin[v/2]}; cur = GaussCurvature[f]; ParametricPlot3D[f, {u, -1.5, 1.5}, {v, 0, 2 Pi}, Boxed -> False, PlotStyle -> Opacity[0.8], ImageSize -> 500, Mesh -> 12, PlotPoints -> 120, MeshFunctions -> Function[{x, y, z, u, v}, Rescale[cur, {-0.04, -0.02}]], ColorFunction -> Function[{x, y, z, u, v}, ColorData["DarkRainbow"][Rescale[cur, {-0.04, -0.02}]]], ColorFunctionScaling -> False]

enter image description here

Comparison with Mean Curvature

A must-read about those jolly times: http://en.wikipedia.org/wiki/Sophie_Germain

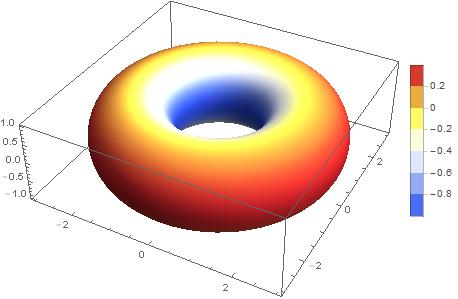
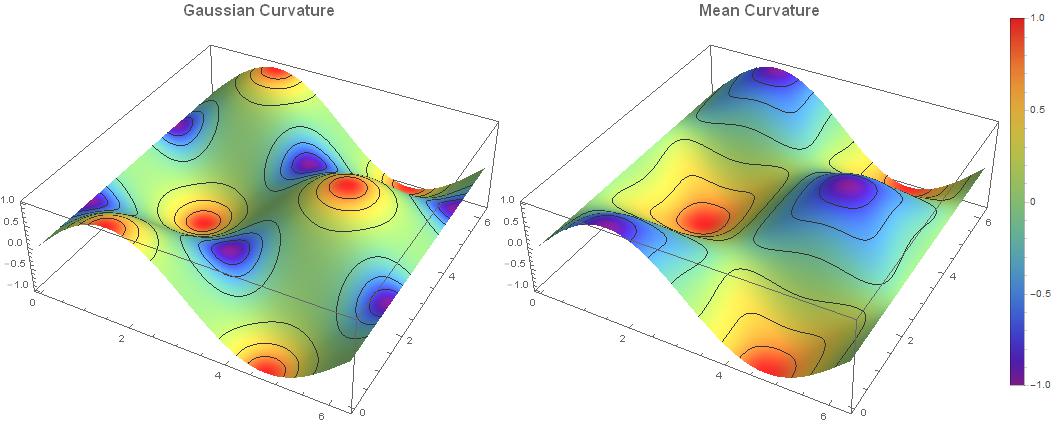
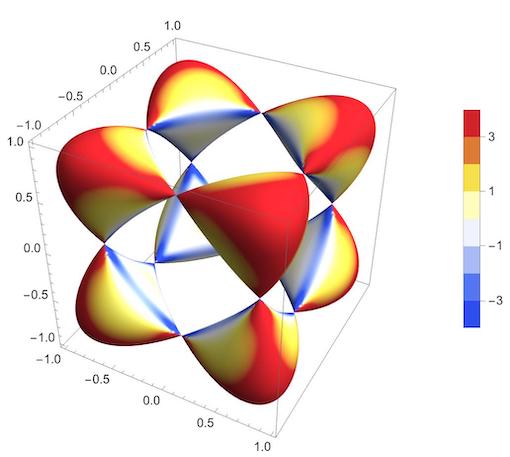
sincos = {u, v, Sin[u] Cos[v]}; cur = GaussCurvature[sincos]; range = Last[PlotRange /. AbsoluteOptions[plo, PlotRange]]; p1 = ParametricPlot3D[sincos, {u, 0, 2 Pi}, {v, 0, 2 Pi}, ImageSize -> 500, Mesh -> 6, PlotLabel -> Style["Gaussian Curvature\n", 16, Bold], PlotPoints -> 120, MeshFunctions -> Function[{x, y, z, u, v}, Rescale[cur, range]], ColorFunction -> Function[{x, y, z, u, v}, ColorData["Rainbow"][Rescale[cur, range]]], ColorFunctionScaling -> False]; MeanCurvature[f_] := With[{du = D[f, u], dv = D[f, v]}, Simplify[(Det[{D[du, u], du, dv}] * dv.dv - 2 Det[{D[f, u, v], du, dv}] * du.dv + Det[{D[dv, v], du, dv}] * du.du) / (2 Simplify[(du.du*dv.dv - (du.dv)^2)]^(3/2))]]; cur = MeanCurvature[sincos]; plo = Plot3D[cur, {u, 0, 2 Pi}, {v, 0, 2 Pi}]; range = Last[PlotRange /. AbsoluteOptions[plo, PlotRange]]; p2 = ParametricPlot3D[sincos, {u, 0, 2 Pi}, {v, 0, 2 Pi}, ImageSize -> 500, Mesh -> 6, PlotLabel -> Style["Mean Curvature\n", 16, Bold], PlotPoints -> 120, MeshFunctions -> Function[{x, y, z, u, v}, Rescale[cur, range]], ColorFunction -> Function[{x, y, z, u, v}, ColorData["Rainbow"][Rescale[cur, range]]], ColorFunctionScaling -> False]; Row[{p1, p2, BarLegend[{"Rainbow", range}, LegendMarkerSize -> 400]}]

enter image description here

Update for space curves

curvature[f_] := With[{d1 = D[f, u], d2 = D[f, {u, 2}]}, Norm[Cross[d1, d2]] / Norm[d1]^3 // Simplify] loxodromes[a_, b_] := { 2 a E^(b u) Cos[u], 2 a E^(b u) Sin[u], a^2 E^(2 b u) - 1 } / (1 + a^2 E^(2 b u)) cur = curvature[loxodromes[1, 0.1]]; plo = Plot[cur, {u, -4 Pi, 4 Pi}, PlotRange -> All]

enter image description here

range = Last[PlotRange /. AbsoluteOptions[plo, PlotRange]]; Show[ ParametricPlot3D[loxodromes[1, 0.1], {u, -4 Pi, 4 Pi}, ColorFunction -> Function[{x, y, z, u, v}, ColorData["Rainbow"][Rescale[cur, range]]], ColorFunctionScaling -> False, PlotStyle -> Thickness[0.01]], Graphics3D[{Opacity[0.2], Sphere[]}], ImageSize -> 500]

enter image description here

A nice novel about Gauss

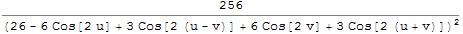
enter image description here

Improve this answer
$\endgroup$
3
  • $\begingroup$ @eldo very nice and thank you for book recommendation...will add to my wish list $\endgroup$ Commented Oct 7, 2014 at 1:40
  • $\begingroup$ @eldo congratulations on 10K! $\endgroup$ Commented Oct 8, 2014 at 9:00
  • $\begingroup$ @ubpdqn Thank you very much for noticing :) $\endgroup$ Commented Oct 8, 2014 at 17:58
6
$\begingroup$

Another expression using Cross

gaussianCurvature[r_, {u_, v_}] := Module[{n, ru = D[r, u], rv = D[r, v], ruv = D[r, u, v]}, n = Cross[ru, rv]; ((D[ru, u].n) (D[rv, v].n) - (ruv.n)^2)/(n.n)^2 // Simplify ]

Examples

gaussianCurvature[{Cos[u] Sin[v], Sin[u] Sin[v], Cos[v]}, {u, v}]

1

Improve this answer
$\endgroup$
0
5
$\begingroup$

Curvatures of implicitly defined surfaces

1. Gaussian curvature

Based upon burnout's answer to this question:

How to speed up estimation of Mean and Gaussian curvatures on triangular meshes?

we can compute the Gaussian curvature of implicitly defined surfaces as follows:

fun = -x^2 + x^4 - y^2 + y^4 - z^2 + z^4; d1 = D[fun, {{x, y, z}}] // Simplify; d2 = D[fun, {{x, y, z}, 2}] // Simplify; gauss[x_, y_, z_] = Simplify[((d1 . LinearSolve[d2, d1]) Det[d2]) / (# . # & [d1])^2]; Legended[ ContourPlot3D[fun == -1/2, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, ColorFunction -> Function[{x, y, z, u, v}, ColorData["TemperatureMap"][Rescale[gauss[x, y, z], {-3, 3}]]], ColorFunctionScaling -> False, Mesh -> False, PlotPoints -> 70], BarLegend[{"TemperatureMap", {-3.1, 3.1}}, Automatic]]

enter image description here

The scaling of {-3, 3} was inserted manually, because I didn't find a way to automate this. But this doesn't take too long. Start with {-1, 1} and go up or down.

2. Mean curvature

The same link also provides a formula for Mean curvature:

fun = -x^2 + x^4 - y^2 + y^4 - z^2 + z^4; d1 = D[fun, {{x, y, z}}] // Simplify; d2 = D[fun, {{x, y, z}, 2}] // Simplify; mcur[x_, y_, z_] = Simplify[(d1 . d2 . d1 - Tr[d2] (# . # &[d1])) / (2 (# . # & [d1])^(3/2))]; Legended[ ContourPlot3D[fun == -1/2, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, ColorFunction -> Function[{x, y, z, u, v}, ColorData["TemperatureMap"][Rescale[Abs @ mcur[x, y, z], {0, 3}]]], ColorFunctionScaling -> False, Mesh -> False, PlotPoints -> 70], BarLegend[{"TemperatureMap", {0, 3.1}}, Automatic]]

enter image description here

3. Mesh lines

The two curvature functions can also be applied to mesh lines:

fun = x^4 + y^4 + z^4 - (x^2 + y^2 + z^2)^2 + 3 (x^2 + y^2 + z^2); d1 = D[fun, {{x, y, z}}] // Simplify; d2 = D[fun, {{x, y, z}, 2}] // Simplify; mcur[x_, y_, z_] = Simplify[(d1 . d2 . d1 - Tr[d2] (# . # & [d1])) / (2 (# . # &[d1])^(3/2))]; Legended[ ContourPlot3D[fun == 3, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, ColorFunction -> Function[{x, y, z, u, v}, ColorData["TemperatureMap"][Rescale[Abs @ mcur[x, y, z], {0, 1}]]], ColorFunctionScaling -> False, Mesh -> 12, MeshFunctions -> Function[{x, y, z, u, v}, Rescale[Abs @ mcur[x, y, z], {0, 1}]], PlotPoints -> 70], BarLegend[{"TemperatureMap", {0, 1.1}}, Automatic]]

enter image description here

Improve this answer
$\endgroup$
1
  • $\begingroup$ In the image transition of double curvature K depicted beautifully. Base faces ( of fattened tetrahedron ) transition with negative K from base towards sides and among side faces with positive K . Perhaps in each corner octant $(0,1)$ it would be clearer. $\endgroup$ Commented Oct 24, 2023 at 20:27

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.