Define and refine mesh around a hole

I am solving Laplace equation with particular geometry and boundary conditions:

L = 10; a = 1; k = 1/2; mesh = 0.06; BoxL = x == L || x == -L || y == L || y == -L; reg = ImplicitRegion[(-L <= x <= L && -L <= y <= L) && (x^2 + y^2 >= a^2), {x, y}]; rp = RegionPlot[reg, AspectRatio -> Automatic, ImageSize -> Tiny] 

Boundary condition for θ

bcθ = {DirichletCondition[u[x, y] == ArcTan[x, y] k, x^2 + y^2 == a^2], DirichletCondition[u[x, y] == 0, BoxL]}; 

Solving equation for θ

θ = NDSolveValue[{Laplacian[u[x, y], {x, y}] == 0, bcθ}, u, {x, y} ∈ reg, Method -> {"FiniteElement", "MeshOptions" -> {MaxCellMeasure -> mesh}, "InterpolationOrder" -> {u -> 2}}]; 

And then plot:

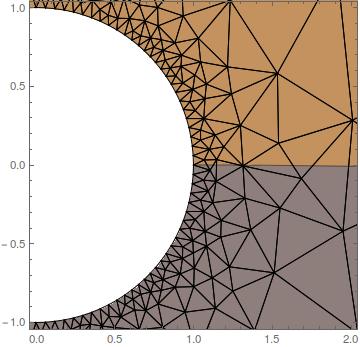
Magnifying and showing the mesh:

There appears to be some small imperfections. Of course I have tuned the parameter mesh to minimize them, i.e., the mesh "scale" is the best I could find within this "shape".

Here comes my question: how do I define a mesh which is finer around the central circular hole (which is a boundary)? Is there a simple way without going down to draw it?

Thanks!