Return to Revisions

Outline

• Issue with application of ConvexHull

• Solution to OP's question

---

Issue with application of ConvexHull

TL;DR : The line segments from ConvexHull seem to pass through points that rest on the same line.

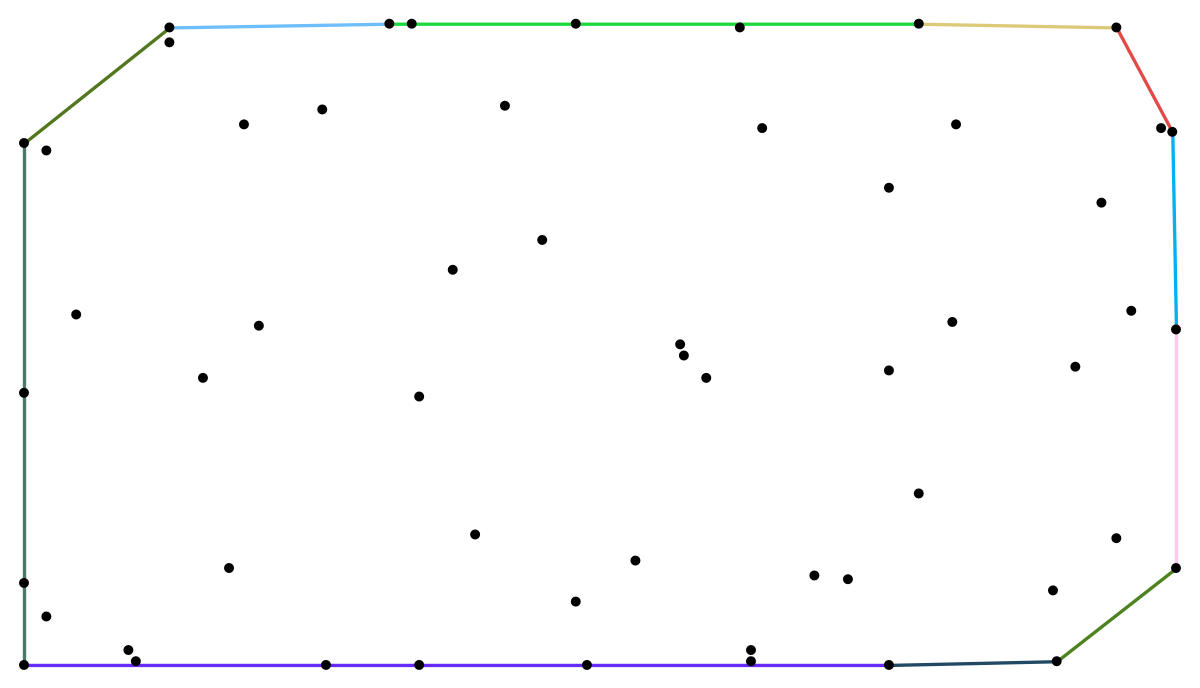
From what I tested, the convex hull mesh does not seem to produce all the edges between graph vertices. See the image below that shows the added line segments from the convex hull:

{GraphEmbedding[g] // ConvexHullMesh // MeshPrimitives[#, 1] & // Map[{RandomColor[], #} &], GraphEmbedding[g] // Map[Point]} // Catenate // Graphics 

This can also be checked with the graph:

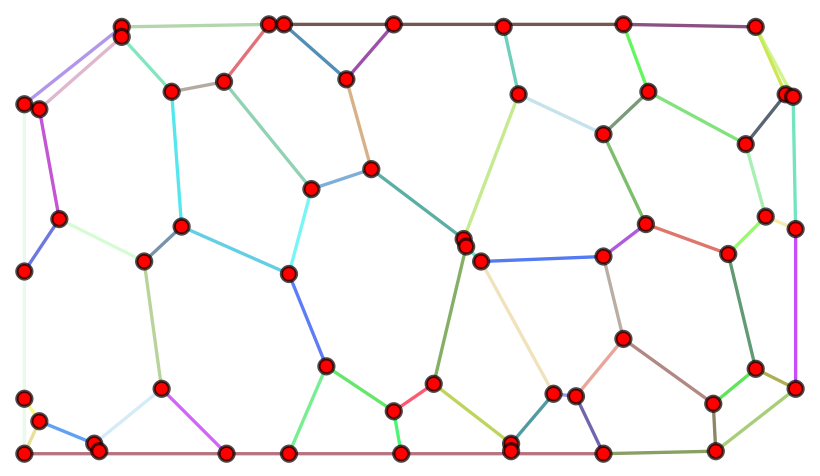
HighlightGraph[new, Style[#, RandomColor[]] & /@ EdgeList@new] 

There are colors that traverse vertices at the boundary.

Also

KVertexConnectedGraphQ[new, 2] 

(* False *)

which OP does not seem to want.

---

Solution to OP's question

TL;DR: Extract degree 1 vertices, use FindCurvePath and PathGraph to connect them and then add them to the original graph with a graph position to geometrical postion mapping

The vertices at the boundary are all degree one vertices. They can be extracted using:

Note: (…=\[Ellipsis])

boundary…vertices = VertexList[g, _?(VertexDegree[g, #] == 1 &)] 

Their geometric positions can be found using the rule:

VertexPos = Thread[VertexList[g] -> GraphEmbedding[g]]; 

Note: (⎵=\[UnderBracket])

boundary…vertices⎵positions = boundary…vertices /. VertexPos; 

One may order these vertices along a path using FindCurvePath

path…ordering = FindCurvePath[boundary…vertices⎵positions]; path = boundary…vertices⎵positions[[path…ordering[[1]]]] 

Then one may construct edges from those ordered points using PathGraph and EdgeList. Note that we first had to order the edges before using PathGraph.

path⎵edges = path // PathGraph // EdgeList; 

Those are written as spatial points we have to convert them back to vertex positions by inverting VertexPos above. We then add those edges to the original graph:

completed…graph = EdgeAdd[g, path⎵edges /. Reverse /@ VertexPos] 

We can check the result with:

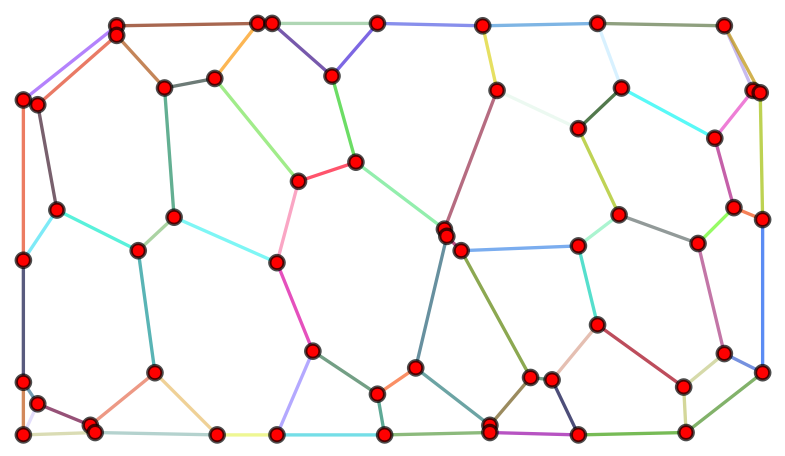
HighlightGraph[completed…graph, Style[#, RandomColor[]] & /@ EdgeList@completed…graph] 

KVertexConnectedGraphQ[completed…graph, 2] 

(* True *)