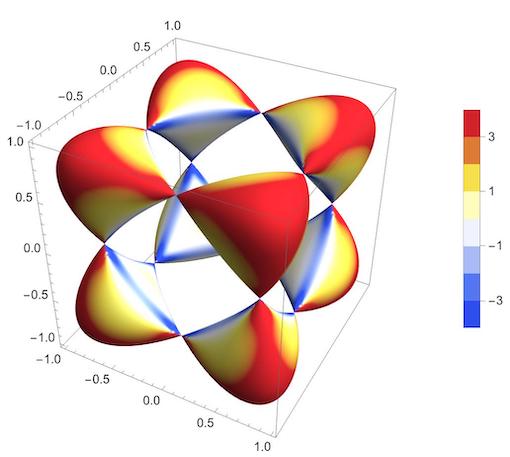
Gaussian curvature of implicitly defined surfaces
Based upon burnout's answer to this question:
How to speed up estimation of mean and Gaussian curvatures on triangular meshes?
we can compute the Gaussian curvature of implicitly defined surfaces as follows:
fun = -x^2 + x^4 - y^2 + y^4 - z^2 + z^4; d1 = D[fun, {{x, y, z}}] // Simplify; d2 = D[fun, {{x, y, z}, 2}] // Simplify; gauss[x_, y_, z_] = Simplify[((d1 . LinearSolve[d2, d1]) Det[d2]) / (# . # & [d1])^2]; Legended[ ContourPlot3D[fun == -1/2, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, ColorFunction -> Function[{x, y, z, u, v}, ColorData["TemperatureMap"][Rescale[gauss[x, y, z], {-3, 3}]]], ColorFunctionScaling -> False, Mesh -> False, PlotPoints -> 70], BarLegend[{"TemperatureMap", {-3.1, 3.1}}, Automatic]] The scaling of {-3, 3} was inserted manually, because I didn't find a way to automate this. But this doesn't take too long. Start with {-1, 1} and go up or down.