19
\$\begingroup\$

Challenge

You are given two distinct bit strings of the same length. (For example, 000 and 111.) Your goal is to find a path from one to the other such that:

  • At each step, you change only one bit (you can go from 000 to any of 001, 010, 100).
  • You cannot visit the same bit string twice.
  • The path is as long as possible, under these constraints.

For example, going from 000 to 111, we can take the path

000, 001, 011, 010, 110, 100, 101, 111

which visits all 8 bit strings of length 3, so it has to be the longest possible.

Rules

  • Standard loopholes apply.
  • You may take the input as two strings of zeroes and ones, or as two arrays of zeroes and ones, or as two arrays of boolean values.
  • You may not take the input as two integers with the right binary representation (writing 000 and 111 as 0 and 7 is not valid).
  • If you want, you may take the length of the bit strings as input.
  • Your program is allowed to output the path by printing the bit strings visited one at a time, or by returning an array of the bit strings visited (each in the same format as the input).
  • Your output should include the start and end of the path (which are your inputs).
  • This is , the shortest code in bytes wins.

Examples

0 1 -> 0, 1 10 01 -> 10, 00, 01 or 10, 11, 01 000 111 -> any of the following: 000, 100, 110, 010, 011, 001, 101, 111 000, 100, 101, 001, 011, 010, 110, 111 000, 010, 110, 100, 101, 001, 011, 111 000, 010, 011, 001, 101, 100, 110, 111 000, 001, 101, 100, 110, 010, 011, 111 000, 001, 011, 010, 110, 100, 101, 111 1001 1100 -> 1001, 0001, 0000, 0010, 0011, 0111, 0101, 0100, 0110, 1110, 1010, 1011, 1111, 1101, 1100 (other paths exist)
Improve this question
\$\endgroup\$
9
  • 1
    \$\begingroup\$ Can we also take boolean values instead of ones and zeros? \$\endgroup\$ Commented Sep 30, 2017 at 19:59
  • \$\begingroup\$ @flawr Sure, that's fine. \$\endgroup\$ Commented Sep 30, 2017 at 20:05
  • \$\begingroup\$ May we assume we will not receive two equal bit-strings (or that we may do anything if so)? \$\endgroup\$ Commented Sep 30, 2017 at 23:00
  • 1
    \$\begingroup\$ @JonathanAllan Yes, let's assume that the bit-strings are not equal. \$\endgroup\$ Commented Sep 30, 2017 at 23:04
  • \$\begingroup\$ Related \$\endgroup\$ Commented Oct 1, 2017 at 0:14

8 Answers 8

Reset to default
6
\$\begingroup\$

Husk, 27 26 24 bytes

→foΛεẊδṁ≠ÖLm↓≠⁰←ġ→PΠmṠe¬

Brute force, so very slow. Try it online!

Explanation

Husk reads naturally from right to left.

←ġ→PΠmṠe¬ Hypercube sequences ending in second input, say y=[1,1,0] mṠe¬ Pair each element with its negation: [[0,1],[0,1],[1,0]] Π Cartesian product: [[0,0,1],[1,0,1],..,[1,1,0]] P Permutations. ġ→ Group by last element ← and take first group. The permutations are ordered so that those with last element y come first, so they are grouped together and returned here. ÖLm↓≠⁰ Find first input. m For each permutation, ↓≠⁰ drop all elements before the first input. ÖL Sort by length. foΛεẊδṁ≠ Check path condition. fo Keep those lists that satisfy: Ẋ For each adjacent pair (e.g. [0,1,0] and [1,1,0]), ṁ take sum of ≠ absolute differences δ of corresponding elements: 1+0+0 gives 1. Λε Each value is at most 1. → Finally, return last element (which has greatest length).
Improve this answer
\$\endgroup\$
4
\$\begingroup\$

Mathematica, 108 bytes

a=#~FromDigits~2+1&;Last@PadLeft[IntegerDigits[#-1,2]&/@FindPath[HypercubeGraph@Length@#,a@#,a@#2,∞,All]]&

Input:

[{0, 0, 0, 0}, {1, 1, 1, 1}]

Output:

{{0, 0, 0, 0}, {0, 0, 0, 1}, {0, 0, 1, 1}, {0, 0, 1, 0}, {0, 1, 1, 0}, {0, 1, 0, 0}, {0, 1, 0, 1}, {1, 1, 0, 1}, {1, 0, 0, 1}, {1, 0, 0, 0}, {1, 1, 0, 0}, {1, 1, 1, 0}, {1, 0, 1, 0}, {1, 0, 1, 1}, {1, 1, 1, 1}}
Improve this answer
\$\endgroup\$
3
\$\begingroup\$

Mathematica, 175 bytes

Nice first question! 

(m=#;n=#2;Last@SortBy[(S=Select)[S[Rest@Flatten[Permutations/@Subsets[Tuples[{0,1},(L=Length)@m]],1],First@#==m&&Last@#==n&],Union[EditDistance@@@Partition[#,2,1]]=={1}&],L])&


Input

[{0, 0, 0}, {1, 1, 1}]

Improve this answer
\$\endgroup\$
0
3
\$\begingroup\$

Haskell, 212 207 bytes

This is probably way too long, but it finally works now. (Thanks to @Lynn for the cartesian product trick!) Thansk @nimi for -5 bytes!

import Data.List b%l=[l++[x|b/=last l,x`notElem`l,1==sum[1|(u,v)<-x`zip`last l,u/=v]]|x<-mapM id$[0>1..]<$b] b!a|f<-nub.concat.((b%)<$>)=snd$maximum$map(length>>=(,))$filter((==b).last)$until(f>>=(==))f[[a]]

Try it online!

Explanation:

b%l -- helper function: -- given a path l (that should end in b) this generates all possible extensions -- of l (if not possible also l itself) x<-mapM id$[0>1..]<$b -- generate all possible vertices of the hypercube -- and check the criteria b/=last l,x`notElem`l,1==sum[1|(u,v)<-x`zip`last l,u/=v] -- extend if possible [l++[x| ... ]| ... ] b!a| -- actual function: -- first define a helper function: f<-nub.concat.((b%)<$>) -- begin with the vertex a and apply the function from above repeatedly -- until you cannot make the path any longer without violating the -- criteria until(f>>=(==))f[[a]] -- only take the paths that actually end in b filter((==b).last)$ -- and find the one with the maximum length =snd$maximum$map(length>>=(,))$
Improve this answer
\$\endgroup\$
3
  • \$\begingroup\$ x<-mapM id$[1>0,1<0]<$b \$\endgroup\$ Commented Oct 1, 2017 at 14:56
  • \$\begingroup\$ ... do you need [True,False]? If [False,True] also works, you can use [0>1..]. \$\endgroup\$ Commented Oct 1, 2017 at 15:00
  • \$\begingroup\$ Oh great, thanks, I didn't know that Bool is Enum, and I forgot that <$ is available (first tried *> which is not in Prelude)! \$\endgroup\$ Commented Oct 1, 2017 at 15:57
3
\$\begingroup\$

Mathematica 116 114 bytes

With several bytes saved thanks to Misha Lavrov.

Last@FindPath[Graph[Rule@@@Cases[Tuples[Tuples[{0,1},{l=Length@#}],{2}],x_/;Count[Plus@@x,1]==1]],##,{1,2^l},Alll]&

Input (8 dimensions)

[{1,0,0,1,0,0,0,1},{1,1,0,0,0,0,1,1}]//AbsoluteTiming

Output (length = 254, after 1.82 seconds)

{1.82393, {{1, 0, 0, 1, 0, 0, 0, 1}, {0, 0, 0, 1, 0, 0, 0, 1}, {0, 0, 0, 0, 0, 0, 0, 1}, {0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 1, 0}, {0, 0,0, 0, 0, 0, 1, 1}, {0, 0, 0, 0, 0, 1, 1, 1}, {0, 0, 0, 0, 0, 1, 0, 1}, {0, 0, 0, 0, 0, 1, 0, 0}, {0, 0, 0, 0, 0, 1, 1, 0}, {0, 0, 0, 0,1, 1, 1,0}, {0, 0, 0, 0, 1, 0, 1, 0}, {0, 0, 0, 0, 1, 0, 0, 0}, {0, 0, 0, 0, 1, 0, 0, 1}, {0, 0, 0, 0, 1, 0, 1, 1}, {0, 0, 0, 0,1, 1, 1, 1}, {0, 0, 0, 0, 1, 1, 0, 1}, {0, 0, 0, 0, 1, 1, 0, 0}, {0, 0, 0, 1, 1, 1, 0, 0}, {0, 0, 0, 1, 0, 1, 0, 0}, {0, 0, 0, 1,0, 0, 0, 0}, {0, 0, 0, 1, 0, 0, 1, 0}, {0, 0, 0, 1, 0, 0, 1, 1}, {0, 0, 0, 1, 0, 1, 1, 1}, {0, 0, 0, 1, 0, 1, 0, 1}, {0, 0, 0, 1, 1, 1, 0, 1}, {0, 0, 0, 1, 1, 0, 0, 1}, {0, 0, 0, 1, 1, 0, 0, 0}, {0, 0, 0, 1, 1, 0, 1, 0}, {0, 0, 0, 1, 1, 0, 1, 1}, {0, 0, 0, 1,1, 1, 1, 1}, {0, 0, 0, 1, 1, 1, 1, 0}, {0, 0, 0, 1, 0, 1, 1, 0}, {0, 0, 1, 1, 0, 1, 1, 0}, {0, 0, 1, 0, 0, 1, 1, 0}, {0, 0, 1, 0,0, 0, 1, 0}, {0, 0, 1, 0, 0, 0, 0, 0}, {0, 0, 1, 0, 0, 0, 0, 1}, {0, 0, 1, 0, 0, 0, 1, 1}, {0, 0, 1, 0, 0, 1, 1, 1}, {0, 0, 1, 0,0, 1, 0, 1}, {0, 0, 1, 0, 0, 1, 0, 0}, {0, 0, 1, 0, 1, 1, 0, 0}, {0, 0, 1, 0, 1, 0, 0, 0}, {0, 0, 1, 0, 1, 0, 0, 1}, {0, 0, 1, 0,1, 0, 1, 1}, {0, 0, 1, 0, 1, 0, 1, 0}, {0, 0, 1, 0, 1, 1, 1, 0}, {0, 0, 1, 0, 1, 1, 1, 1}, {0, 0, 1, 0, 1, 1, 0, 1}, {0, 0, 1, 1,1, 1, 0, 1}, {0, 0, 1, 1, 0, 1, 0, 1}, {0, 0, 1, 1, 0, 0, 0, 1}, {0, 0, 1, 1, 0, 0, 0, 0}, {0, 0, 1, 1, 0, 0, 1, 0}, {0, 0, 1, 1,0, 0, 1, 1}, {0, 0, 1, 1, 0, 1, 1,1}, {0, 0, 1, 1, 1, 1, 1, 1}, {0, 0, 1, 1, 1, 0, 1, 1}, {0, 0, 1, 1, 1, 0, 0, 1}, {0, 0, 1, 1,1, 0, 0, 0}, {0, 0, 1, 1, 1, 0, 1, 0}, {0, 0, 1, 1, 1, 1, 1, 0}, {0, 0, 1, 1, 1, 1, 0, 0}, {0, 0, 1, 1, 0, 1, 0, 0}, {0, 1, 1, 1,0, 1, 0, 0}, {0, 1, 0, 1, 0, 1, 0, 0}, {0, 1, 0, 0, 0, 1, 0, 0}, {0, 1, 0, 0, 0, 0, 0, 0}, {0, 1, 0, 0, 0, 0, 0, 1}, {0, 1, 0, 0,0, 0, 1, 1}, {0, 1, 0, 0, 0, 0, 1, 0}, {0, 1, 0, 0, 0, 1, 1, 0}, {0, 1, 0, 0, 0, 1, 1, 1}, {0, 1, 0, 0, 0, 1, 0, 1}, {0, 1, 0, 0,1, 1, 0, 1}, {0, 1, 0, 0, 1, 0, 0, 1}, {0, 1, 0, 0, 1, 0, 0, 0}, {0, 1, 0, 0, 1, 0, 1, 0}, {0, 1, 0, 0, 1, 0, 1, 1}, {0, 1, 0, 0,1, 1, 1, 1}, {0, 1, 0, 0, 1, 1, 1, 0}, {0, 1, 0, 0, 1, 1, 0,0}, {0, 1, 0, 1, 1, 1, 0, 0}, {0, 1, 0, 1, 1, 0, 0, 0}, {0, 1, 0, 1,0, 0, 0, 0}, {0, 1, 0, 1, 0, 0, 0, 1}, {0, 1, 0, 1, 0, 0, 1, 1}, {0, 1, 0, 1, 0, 0, 1, 0}, {0, 1, 0, 1, 0, 1, 1, 0}, {0, 1, 0, 1,0, 1, 1, 1}, {0, 1, 0, 1, 0, 1, 0, 1}, {0, 1, 0, 1, 1, 1, 0, 1}, {0, 1, 0, 1, 1, 0, 0, 1}, {0, 1, 0, 1, 1, 0, 1, 1}, {0, 1, 0, 1,1, 0, 1, 0}, {0, 1, 0, 1, 1, 1, 1, 0}, {0, 1, 0, 1, 1, 1, 1, 1}, {0, 1, 1, 1, 1, 1, 1, 1}, {0, 1, 1, 0, 1, 1, 1, 1}, {0, 1, 1, 0,0, 1, 1, 1}, {0, 1, 1, 0, 0, 0, 1, 1}, {0, 1, 1, 0, 0, 0, 0, 1}, {0, 1, 1, 0, 0, 0, 0, 0}, {0, 1, 1, 0, 0, 0, 1, 0}, {0, 1, 1, 0,0, 1, 1, 0}, {0, 1, 1, 0, 0, 1, 0, 0}, {0, 1, 1, 0, 0, 1, 0, 1}, {0, 1, 1, 0, 1, 1, 0, 1}, {0, 1, 1, 0, 1, 0, 0, 1}, {0, 1, 1, 0,1, 0, 0, 0}, {0, 1, 1, 0, 1, 0, 1, 0}, {0, 1, 1, 0, 1, 0, 1, 1}, {0, 1, 1, 1, 1, 0, 1, 1}, {0, 1, 1, 1, 0, 0, 1, 1}, {0, 1, 1, 1,0, 0, 0, 1}, {0, 1, 1, 1, 0, 0, 0, 0}, {0, 1, 1, 1, 0, 0, 1, 0}, {0, 1, 1, 1, 0, 1, 1, 0}, {0, 1, 1, 1, 0, 1, 1, 1}, {0, 1, 1, 1,0, 1, 0, 1}, {0, 1, 1, 1, 1, 1, 0, 1}, {0, 1, 1, 1, 1, 0, 0, 1}, {0, 1, 1, 1, 1, 0, 0, 0}, {0, 1, 1, 1, 1, 0, 1, 0}, {0, 1, 1, 1,1, 1, 1, 0}, {0, 1, 1, 0, 1, 1, 1, 0}, {0, 1, 1, 0, 1, 1, 0, 0}, {0, 1, 1, 1, 1, 1, 0, 0}, {1, 1, 1, 1, 1, 1, 0, 0}, {1, 0, 1, 1,1, 1, 0, 0}, {1, 0, 0, 1, 1, 1, 0, 0}, {1, 0, 0, 0, 1, 1, 0, 0}, {1, 0, 0, 0, 0, 1, 0, 0}, {1, 0, 0, 0, 0, 0, 0, 0}, {1, 0, 0, 0,0, 0, 0, 1}, {1, 0, 0, 0, 0, 0, 1, 1}, {1, 0, 0, 0, 0, 0, 1, 0}, {1, 0, 0, 0, 0, 1, 1, 0}, {1, 0, 0, 0, 0, 1, 1, 1}, {1, 0, 0, 0,0, 1, 0, 1}, {1, 0, 0, 0, 1, 1, 0, 1}, {1, 0, 0, 0, 1, 0, 0, 1}, {1, 0, 0, 0, 1, 0, 0, 0}, {1, 0, 0, 0, 1, 0, 1, 0}, {1, 0, 0, 0,1, 0, 1, 1}, {1, 0, 0, 0, 1, 1, 1, 1}, {1, 0, 0, 0, 1, 1, 1, 0}, {1, 0, 0, 1, 1, 1, 1, 0}, {1, 0, 0, 1, 0, 1, 1, 0}, {1, 0, 0, 1,0, 0, 1, 0}, {1, 0, 0, 1, 0, 0, 0, 0}, {1, 0, 0, 1, 0, 1, 0, 0}, {1, 0, 0, 1, 0, 1, 0, 1}, {1, 0, 0, 1, 0, 1, 1, 1}, {1, 0, 0, 1,0, 0, 1, 1}, {1, 0, 0, 1, 1, 0, 1, 1}, {1, 0, 0, 1, 1, 0, 0, 1}, {1, 0, 0, 1, 1, 0, 0, 0}, {1, 0, 0, 1, 1, 0, 1, 0}, {1, 0, 1, 1,1, 0, 1, 0}, {1, 0, 1, 0, 1, 0, 1, 0}, {1, 0, 1, 0, 0, 0, 1, 0}, {1, 0, 1, 0, 0, 0, 0, 0}, {1, 0, 1, 0, 0, 0, 0, 1}, {1, 0, 1, 0,0, 0, 1, 1}, {1, 0, 1, 0, 0, 1, 1, 1}, {1, 0, 1, 0, 0, 1, 0, 1}, {1, 0, 1, 0, 0, 1, 0, 0}, {1, 0, 1, 0, 0, 1, 1, 0}, {1, 0, 1, 0,1, 1, 1, 0}, {1, 0, 1, 0, 1, 1, 0, 0}, {1, 0, 1, 0, 1, 0, 0, 0}, {1, 0, 1, 0, 1, 0, 0, 1}, {1, 0, 1, 0, 1, 0, 1, 1}, {1, 0, 1, 0,1, 1, 1, 1}, {1, 0, 1, 0, 1, 1, 0, 1}, {1, 0, 1, 1, 1, 1, 0, 1}, {1, 0, 0, 1, 1, 1, 0, 1}, {1, 0, 0, 1, 1, 1, 1, 1}, {1, 0, 1, 1,1, 1, 1, 1}, {1, 0, 1, 1, 0, 1, 1, 1}, {1, 0, 1, 1, 0, 0, 1, 1}, {1, 0, 1, 1, 0, 0, 0, 1}, {1, 0, 1, 1, 0, 0, 0, 0}, {1, 0, 1, 1,0, 0, 1, 0}, {1, 0, 1, 1, 0, 1, 1, 0}, {1, 0, 1, 1, 0, 1, 0, 0}, {1, 0, 1, 1, 0, 1, 0, 1}, {1, 1, 1, 1, 0, 1, 0, 1}, {1, 1, 0, 1,0, 1, 0, 1}, {1, 1, 0, 0, 0, 1, 0,1}, {1, 1, 0, 0, 0, 0, 0, 1}, {1, 1, 0, 0, 0, 0, 0, 0}, {1, 1, 0, 0, 0, 0, 1, 0}, {1, 1, 0, 0,0, 1, 1, 0}, {1, 1, 0, 0, 0, 1, 0, 0}, {1, 1, 0, 0, 1, 1, 0, 0}, {1, 1, 0, 0, 1, 0, 0, 0}, {1, 1, 0, 0, 1, 0, 0, 1}, {1, 1, 0, 0,1, 0, 1, 1}, {1, 1, 0, 0, 1, 0, 1, 0}, {1, 1, 0, 0, 1, 1, 1, 0}, {1, 1, 0, 0, 1, 1, 1, 1}, {1, 1, 0, 0, 0, 1, 1, 1}, {1, 1, 0, 1,0, 1, 1, 1}, {1, 1, 0, 1, 0, 0, 1, 1}, {1, 1, 0, 1, 0, 0, 0, 1}, {1, 1, 0, 1, 0, 0, 0, 0}, {1, 1, 0, 1, 0, 0, 1, 0}, {1, 1, 0, 1,0, 1, 1, 0}, {1, 1, 0, 1, 0, 1, 0, 0}, {1, 1, 0, 1, 1, 1, 0, 0}, {1, 1, 0, 1, 1, 0, 0, 0}, {1, 1, 0, 1, 1, 0, 0, 1}, {1, 1, 0, 1,1, 0, 1, 1}, {1, 1, 0, 1, 1, 0, 1, 0}, {1, 1, 0, 1, 1, 1, 1, 0}, {1, 1, 0, 1, 1, 1, 1, 1}, {1, 1, 0, 1, 1, 1, 0, 1}, {1, 1, 0, 0,1, 1, 0, 1}, {1, 1, 1, 0, 1, 1, 0, 1}, {1, 1, 1, 0, 0, 1, 0, 1}, {1, 1, 1, 0, 0, 0, 0, 1}, {1, 1, 1, 0, 0, 0, 0, 0}, {1, 1, 1, 0,0, 0, 1, 0}, {1, 1, 1, 0, 0, 1, 1, 0}, {1, 1, 1, 0, 0, 1, 0, 0}, {1, 1, 1, 0, 1, 1, 0, 0}, {1, 1, 1, 0, 1, 0, 0, 0}, {1, 1, 1, 0,1, 0, 0, 1}, {1, 1, 1, 0, 1, 0, 1, 1}, {1, 1, 1, 0, 1, 0, 1, 0}, {1, 1, 1, 0, 1, 1, 1, 0}, {1, 1, 1, 0, 1, 1, 1, 1}, {1, 1, 1, 0,0, 1, 1, 1}, {1, 1, 1, 1, 0, 1, 1, 1}, {1, 1, 1, 1, 0, 1, 1, 0}, {1, 1, 1, 1, 0, 0, 1, 0}, {1, 1, 1, 1, 0, 0, 0, 0}, {1, 1, 1, 1,0, 0, 0, 1}, {1, 1, 1, 1, 1, 0, 0, 1}, {1, 1, 1, 1, 1, 1, 0, 1}, {1, 1, 1, 1, 1, 1, 1, 1}, {1, 1, 1, 1, 1, 1, 1, 0}, {1, 1, 1, 1,1, 0, 1, 0}, {1, 1, 1, 1, 1, 0, 0, 0}, {1, 0, 1, 1, 1, 0, 0, 0}, {1, 0, 1, 1, 1, 0, 0, 1}, {1, 0, 1, 1, 1, 0, 1, 1}, {1, 1, 1, 1,1, 0, 1, 1}, {1, 1, 1, 1, 0, 0, 1, 1}, {1, 1, 1, 0, 0, 0, 1, 1}, {1, 1, 0, 0, 0, 0, 1, 1}}}

Tuples[{0,1},{l=Length@#}],{2}]& generates the numbers 0...8 as binary lists.

The outer Tuples...{2} produces all ordered pairs of those binary numbers.

Plus@@x sums each of the pairs, generating triplets of 0, 1.

Cases....Count[Plus@@x, 1]==1 returns all of the sums that contain a single 1. These arise when the two original binary numbers are connected by an edge.

Rules connects the vertices of the graph, each vertex being a binary number.

Graph creates a graph corresponding to said vertices and edges.

FindPath finds up to 2^n paths connecting vertex a to vertex b, the given numbers.

Last takes the longest of these paths.

For three dimensions, the graph can be represented in a plane as shown here:

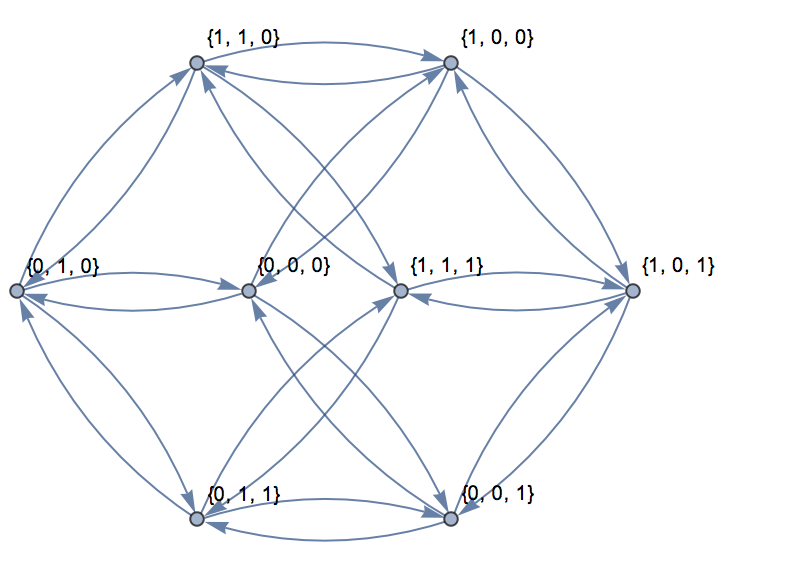
graph flat

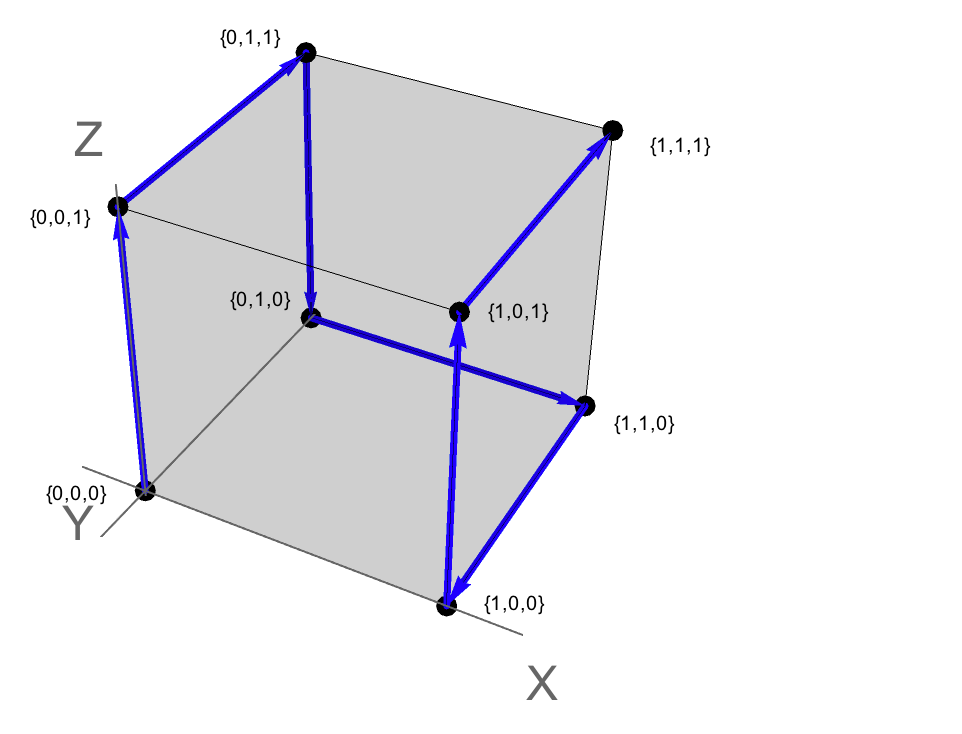
For the input, {0,0,0}, {1,1,1}, the following is output:

{{{0, 0, 0}, {0, 0, 1}, {0, 1, 1}, {0, 1, 0}, {1, 1, 0}, {1, 0, 0}, {1, 0, 1}, {1, 1, 1}}}

This path can be found in the above graph.

It can also be conceived as the following path in 3-space, where each vertex corresponds to a point {x,y,z}. {0,0,0} represents the origin and {1,1,1} represents the "opposite" point in a unit cube.

So the solution path corresponds to a traversal of edges along the unit cube. In this case, the path is Hamiltonian: it visits each vertex one time (i.e. with no crossings and no vertices omitted).

g4

Improve this answer
\$\endgroup\$
7
  • \$\begingroup\$ Is there a simple reason why 2^n paths from a to b are enough paths for the longest one of them to be the longest overall? \$\endgroup\$ Commented Oct 4, 2017 at 22:03
  • \$\begingroup\$ @Misha, A very good question. \$\endgroup\$ Commented Oct 4, 2017 at 22:54
  • \$\begingroup\$ Here's one way to think about it. The longest path, a Hamiltonian path, will be one less than the number of corners. (We're counting the number of edges on the path.) The number of corners is 2 ^n. So the max path length would be 2^n-1. \$\endgroup\$ Commented Oct 5, 2017 at 3:14
  • \$\begingroup\$ I agree that the maximum path length always visits either 2^n vertices (if it's Hamiltonian) or 2^n-1 vertices (if a Hamiltonian path is impossible due to parity). That's different from my question, which is: why does generating 2^(n+2) (I guess 2^n was the wrong number) different paths (some of which may be very short) guarantee that the longest of them will be the longest of all different paths. \$\endgroup\$ Commented Oct 5, 2017 at 3:21
  • \$\begingroup\$ In other words, why the 2^(l+2) in your code? \$\endgroup\$ Commented Oct 5, 2017 at 3:22
3
\$\begingroup\$

Haskell, 141 123 bytes

c(a:b)=(1-a:b):map(a:)(c b) c _=[] q#z=[z]:[z:s|w<-c z,notElem w q,s<-(w:q)#w] x!y=snd$maximum[(p*>x,p)|p<-[x]#x,last p==y]

Uses lists of integers. Try it online!

Explanation

The main function is !, and the auxiliary functions are # and c. Given a list of bits, c gives all possible ways of flipping one of them, e.g. [0,1,1] -> [[1,1,1],[0,0,1],[0,1,0]].

c(a:b)= -- c on nonempty list with head a and tail b is (1-a:b): -- the list with negated a tacked to b, then map(a:)(c b) -- c applied recursively to b, with a tacked to each of the results. c _=[] -- c on empty list gives an empty list.

The function # takes a list of lists (the "memory") and a list (the "initial bitstring"). It constructs all hypercube paths that begin with the initial element, contain only distinct bitstrings, and do not step on the strings in the memory.

q#z= -- # on memory q and initial string z is [z]: -- the singleton path [z], and [z:s| -- z tacked to each path s, where w<-c z, -- w is obtained by flipping a bit of z, notElem w q, -- w is not in the memory, and s<-(w:q)#w] -- s is a path starting from w that avoids w and all elements of q.

The main function ! ties it all together. A trick I use here is p*>x (x repeated length p times) instead of length p. Since longer repetitions of x come later in the natural ordering of lists, maximum chooses the longest path in either case, since the first coordinates of pairs are compared before the second ones.

x!y= -- ! on inputs x and y is snd$maximum -- the second element of the maximal pair in [(p*>x,p)| -- the list of pairs (p*>x,p), where p<-[x]#x, -- p is a path starting from x that avoids stepping on x, and last p==y] -- p ends in y.
Improve this answer
\$\endgroup\$
2
\$\begingroup\$

Jelly,  25  27 bytes

+2 bytes to fix a bug with my golfing :( hopefully I'll find a shorter way though.

ṫi¥³ḣi L2ṗŒ!瀵ạ2\S€ỊẠ×LµÞṪ

A full program taking the bit-strings using 1 and 2* as lists. The arguments are from and to. The program prints a list of lists of the same.

* 0 and 1 may be used instead at the cost of a byte (add ’ between L2ṗ and Œ!ç€... to decrement).

Try it online!

How?

updating...

ṫi¥³ḣi - Link 1, getSlice: list of lists, bitstrings; list, toBitstring ³ - get 3rd command line argument (fromBitstring) ¥ - last two links as a dyad: i - index (of fromBitstring in bitstrings) ṫ - tail (bitstrings) from (that) index i - index (of toBitstring in that result) ḣ - head to (that) index L2ṗŒ!瀵ạ2\S€ỊẠ×LµÞṪ - Main link: list, fromBitstring; list, toBitstring L - length (of fromBitstring) 2 - literal two ṗ - Cartesian power (of implicit range(2)=[1,2] with L(fromBitstring)) - ...i.e. all unique bitstrings of the required length (using [1,2]) Œ! - all permutations (of that list) ç€ - call the last link (1) as a dyad (i.e. f(that, toBitstring)) µ µÞ - sort by the monadic function: 2\ - 2-wise reduce with: ạ - absolute difference S€ - sum €ach Ị - insignificant (vectorises) (abs(z)<=1 - for our purposes it's really just used for z==1 since only positive integers are possible) Ạ - all truthy? (1 if so 0 otherwise) L - length × - multiply Ṫ - tail (the last one is one of the maximal results) - implicit print
Improve this answer
\$\endgroup\$
3
  • \$\begingroup\$ How Jelly works is a mystery to me, but an input of [1,1] and [2,2] produces output of [[1, 1], [2, 1], [1, 2], [2, 2]] when I Try It Online, which isn't a valid path. \$\endgroup\$ Commented Sep 30, 2017 at 23:16
  • \$\begingroup\$ Hmm I must have done something wrong - looking... \$\endgroup\$ Commented Sep 30, 2017 at 23:33
  • \$\begingroup\$ OK fixed by reverting one of my golfs for 2 bytes. \$\endgroup\$ Commented Sep 30, 2017 at 23:39
0
\$\begingroup\$

Python3, 182 bytes

def f(a,b): q,s=[(a,[a])],[] for a,c in q: if a==b:s+=[c];continue q+=[(u,c+[u])for i,j in enumerate(a)if(u:=a[:i]+str(int(not int(j)))+a[i+1:])not in c] return max(s,key=len)

Try it online!

Improve this answer
\$\endgroup\$
1
  • \$\begingroup\$ 168 bytes \$\endgroup\$ Commented Aug 29 at 18:00

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.