JavaScript, 569 537 495 442 characters (ASCII)

h="";M=Math;Z=M.max;Y=M.min;function d(a,b,r,s,t){n=M.sqrt(a*a+e*e);return n-(r+M.abs((M.atan2(a,e )/M.PI*b+t)%1-0.5)*s*n)}f=parseInt(prompt(),10);for(g=0;g<f;g++){for(k=0;k<2*f;k++)e=k/(0.5*f)-0.8 ,q=g/(0.25*f),u=q-1.08,v=q-1.29,z=e*e+u*u-0.3364,E=Z(-e-0.8,Y(Z(0.62*e+0.8-q,-2.06+q),Z(1*e+0.8+ 0.85-q,-3.87+q))),p=0>Y(d(q-2.91,6,0.38,0.7,10),Y(Z(e*e+v*v-0.3025,-z),Z(d(q-1.54,8,0.25,0.6,10.5) ,q-1.7)))?" ":-0.13>E?";":0>=E?"8":"",h+=p;h+="\n"}h 

To run : copy-paste to browser console (eg: Chrome developer tools or Firebug)

Result :

8 8888 8888888 8888;88888 8888;;;;88888 8888;;;;;;;888888 8888;;;;;;;;;;;88888 8888;;;;;;;;;;;;;;88888 8888;;;;;;;;;;;;;;;;;88888 8888;;;;;;;;;;;;;;;;;;;;888888 8888;;;;;;;;;;;;;;;;;;;;;;;;88888 8888;;;;;;;;;;;;;;;;;;;;;;;;;;;88888 8888;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;88888 8888;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;88888 8888;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;888888 8888;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;88888 8888;;;;;;;;;;;; ; ; ; ;;;;;;;;;;;;;;;;;;;;;;88888 8888;;; ;;;;; ;;;;; ;;;;;;;;;;;;;;;;88888 8888;;; ;;;;;; ;;;;;; ;;;;;;;;;;;;;;;;;;;888888 8888;;;; ;;; ;;; ;;;;;;;;;;;;;;;;;;;;;;;;88888 8888;;;;; ;;;;;;;;;;;;;;;;;;;;;;;;;;;;88888 8888;;;;;;; ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;88888 8888;;;;;;;;; ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;88888 8888;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;888888 8888;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;88888 8888;;;;;;;;;;;;;;;;;;;;;;8888888888888888888888888888888888888888888888888888888 8888;;;;;;;;;;;;;;;;;;;;;;;;888 8888;;;;;;;;;;;;;;;;;;;;;;;;;;888 8888;;;;;;;;;;;;;;;;;;;;;;;;;;;;888 8888;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;888 8888;;;;;;;;;;;;;;;; ;;;;;;;;;;;;;;;888 8888;;;;;;;;; ;;; ;;; ;;;;;;;;;;888 8888;;;;;;;;;; ;;;;;;;;;;;;;888 8888;;;; ;;;;;;;;;888 8888;;;;;; ;;;;;;;;;;;;;888 8888;;;;;;; ;;;;;;;;;;;;;;;;888 8888;;; ;;;;;;;;;;;;;;888 8888;;;;; ;;;;;;;;;;;;;;;;;;888 8888;;;;;;; ;;;;;;;;;;;;;;;;;;;;;;888 8888;;;;; ;;;;;;;;;;;;;;;;;;;;;;888 8888;;;; ;;;;; ;;;;; ;;;;;;;;;;;;;;;;;;;;;;;888 8888;;;;;;;;; ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;888 8888;;;;;;;;; ;;;; ;;;; ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;888 8888;;;;;;;;;;;;;;;; ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;888 8888;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;888 8888;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;888 8888;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;888 8888888888888888888888888888888888888888888888888888888888888888888888888 888888888888888888888888888888888888888888888888888888888888888888888888888 

EDIT : added height as user input as ST3 suggested. it works best with big values (eg : 120)

Mathematica

Nepal's Interim Constitution - Schedule 1 (rel. to Article 6), pp. 260 and 262, provides 25 detailed instructions about how to construct the flag. (see http://www.ccd.org.np/resources/interim.pdf). The numbers in the comments refer to the corresponding instructions in the constitution.

We will need functions to draw equilateral triangles and determine the distance from a point to a line:

ClearAll[triangle] triangle[a_?NumericQ,b_?NumericQ,c_?NumericQ,labeled_:True]:= Block[{x,y,pt,sqr},sqr=#.#&; pt[a1_,b1_,c1_]:=Reduce[sqr[{x,y}]==b1^2&&sqr[{x,y}-{a1,0}]==c1^2&&y>0,{x,y}]; {( (*Polygon[{{0,0},{a,0},{x,y}}]*) Polygon[{{-a/2(*0*),0},{a/2,0},{x-a/2,y}}]), If[labeled, {Text[Style[Framed[a,Background->LightYellow],11],{a/2,0}], Text[Style[Framed[b,Background->LightYellow],11],{x/2,y/2}], Text[Style[Framed[c,Background->LightYellow],11],{(a+x)/2,y/2}]},{}]}/.ToRules[pt[a,b,c]]] (*distance from point to a line *) dist[line_,{x0_,y0_}]:=(Abs[a x0+b y0+c]/.{x0-> m[[1]],y0-> m[[2]]})/Sqrt[a^2+b^2]; (* used below *) 

The remaining code, with numbers referring to the instructions. By far, the most challenging part is to make the rays for the moon and the sun. GeometricalTransformation comes in handy for doing translations and rotations.

 (*shape inside flag*) (*1*) w=100;a={0,0};b={w,0}; lAB=Line[{a,b}]; tA=Text["A",Offset[{-10,-20},a]]; tB=Text["B",Offset[{20,-20},b]]; (*2*) c={0,w 4/3};d={0,w}; lAC=Line[{a,c}]; tC=Text["C",Offset[{-10,20},c]]; lAD=Line[{a,d}]; tD=Text["D",Offset[{-10,0},d]]; lBD=Line[{b,d}]; (*3*) e=Solve[(x-w)^2+y^2==(w)^2&&y==w-x,{x,y}][[1,All,2]]; tE=Text["E",Offset[{15,0},e]]; (*4*) f={0,e[[2]]};tF=Text["F",Offset[{-10,0},f]]; g={w,e[[2]]};tG=Text["G",Offset[{15,0},g]]; lFG=Line[{f,g}]; poly={a,b,e,g,c}; (*5*)lCG= Line[{c,g}]; (*moon*) (*6*) lineCG=N[((f[[2]]-c[[2]])/w)x+c[[2]](*100*)]; h={w/4,0};tH=Text["H",Offset[{0,-20},h]]; i={h[[1]],lineCG/.x->h[[1]]};tI=Text["I",Offset[{10,0},i]]; lHI={Dashed, LightGray,Line[{h,i}]}; (*7*) j={0,f[[2]]+(c[[2]]-f[[2]])/2};tJ=Text["J",Offset[{-10,10},j]]; lineJG=N[((f[[2]]-j[[2]])/g[[1]])x+j[[2]]]; k={Solve[lineCG==j[[2]],x][[1,1,2]],j[[2]]};tK=Text["K",Offset[{10,10},k]]; (*k={Solve[lineCG\[Equal]c[[2]],x][[1,1,2]],j[[2]]};tK=Text["K",Offset[{10,10},k]];*) lJK={Dashed, LightGray,Line[{j,k}]}; (*8*)l={i[[1]],j[[2]]};tL=Text["L",Offset[{0,10},l]]; (*9*)lJG={LightGray,Dashed,Line[{j,g}]}; (*10*)m={h[[1]],(lineJG/.x-> h[[1]])};tM=Text["M",Offset[{0,10},m]]; (*11*)distMfromBD=dist[{1,1,-w(*100*)},m]; n={i[[1]],m[[2]]-distMfromBD};tN=Text["N",Offset[{0,0},n]]; (*ln=Abs[l[[2]]-n[[2]]];*) (*12*)o={0,m[[2]]};tO=Text["O",Offset[{-10,0},o]]; lM={Dashed,LightGray,Line[{o,{g[[1]],o[[2]]}}]}; (*13*) radiusLN=l[[2]]-n[[2]]; p={m[[1]]-radiusLN,m[[2]]};tP=Text["P",Offset[{0,10},p]]; q={m[[1]]+radiusLN,m[[2]]};tQ=Text["Q",Offset[{0,10},q]]; moonUpperEdge={White,Circle[l,radiusLN,{Pi,2 Pi}]}; moonLowerEdge={White,Circle[m,radiusMQ,{Pi,2 Pi}]}; (*14*)radiusMQ=q[[1]]-m[[1]]; (*15*)radiusNM=m[[2]]-n[[2]]; arc={Yellow,Circle[n,radiusNM,{Pi/7,6 Pi/7}]}; {r,s}=Solve[(x-l[[1]])^2+(y-l[[2]])^2==(radiusLN)^2 &&(x-n[[1]])^2+(y-n[[2]])^2==(radiusNM)^2,{x,y}][[All,All,2]]; tR=Text["R",Offset[{0,0},r]]; tS=Text["S",Offset[{0,0},s]]; t={h[[1]],r[[2]]}; tT={Black,Text["T",Offset[{0,0},t]]}; (*16*)radiusTS=Abs[t[[1]]-s[[1]]]; (*17*)radiusTM=Abs[t[[2]]-m[[2]]]; (*18 triangles*) t2=Table[GeometricTransformation[GeometricTransformation[triangle[4,4,4,False][[1]],RotationTransform[k Pi/8]],{TranslationTransform[t]}],{k,-4,3}]; midRadius=(Abs[radiusTM+radiusTS]/2-2); pos=1;table2=GeometricTransformation[t2[[pos++]],{TranslationTransform[#]}]&/@Table[midRadius {Cos@t,Sin[t]},{t,Pi/16,15 Pi/16,\[Pi]/8}]; (*19 sun*)u={0,f[[2]]/2};tU=Text["U",Offset[{-10,0},u]]; lineBD=N[(d[[2]]/w)x+d[[2]]]; v={-Solve[lineBD==u[[2]],x][[1,1,2]],u[[2]]};tV=Text["V",Offset[{10,0},v]]; lUV={LightGray,Dashed,Line[{u,v}]}; (*20*)w={h[[1]],u[[2]]};tW={Black,Text["W",Offset[{0,0},w]]}; (*21*) (*22*) t3=Table[GeometricTransformation[GeometricTransformation[triangle[9,9,9,False][[1]],RotationTransform[k Pi/6]],{TranslationTransform[w]}],{k,-3,9}]; midRadius3=(Abs[radiusTM+radiusTS]/2+2.5); pos=1; table3=GeometricTransformation[t3[[pos++]],{TranslationTransform[#]}]&/@Table[midRadius3 {Cos@t,Sin[t]},{t,0,2 Pi,2\[Pi]/12}]; Show[ Graphics[{Gray, (*1*)lAB,tA,tB, (*2*)lAC,tC,lAD,tD,lBD, (*3*)tE, (*4*)tF,lFG,tG,{Red,Opacity[.4],Polygon[poly]}, (*5*)lCG, (*6*)tH,lCG,tI,lHI, (*7*)tJ,lJK,tK, (*8*)tL, (*9*)lJG, (*10*)tM, (*11*)tN, (*12*)lM,tO, (*13*)moonUpperEdge,tP,tQ, (*14*)moonLowerEdge, (*15*)arc,tR,tS,tT, (*16*){White,Dashed,Circle[t,radiusTS(*,{0, Pi}*)]}, (*17*){White,Opacity[.5],Disk[t,radiusTM,{0, 2 Pi}]}, (*18 triangles*){White,(*EdgeForm[Black],*)table2}, (*19 sun*)tU,tV,lUV, (*20*)tW,{Opacity[.5],White,Disk[w,Abs[m[[2]]-n[[2]]]]}, (*21*)Circle[w,Abs[l[[2]]-n[[2]]]], (*22*){Black(*White*),EdgeForm[Black],triangle[4,4,4,False](*table3*)}, {White,(*EdgeForm[Black],*)table3}, (*23*) {Darker@Blue,Thickness[.03],Line[{a,b,e,g,c,a}]} }, Ticks-> None(*{{0,100},{0,80,120,130}}*), BaseStyle-> 16,AspectRatio-> 1.3,Axes-> True], (*cresent moon*) RegionPlot[{(x-25)^2+(y-94.19)^2<21.4^2&&(x-25)^2+(y-102.02)^2>21.4^2},{x,0,100},{y,30,130},PlotStyle->{Red,White}]] 

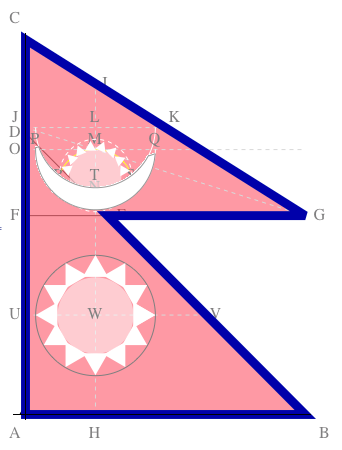
The following flag, from the above code, is made according to the instructions in the constitution.

Colors are modified to enable easier viewing of the construction lines. The letters refer to points and lines in the instructions.

By the way, flags of the world can be called up directly within Mathematica. For example:

Graphics[CountryData["Nepal", "Flag"][[1]], ImageSize->{Automatic,200}] 

Python

import turtle, sys from math import sqrt, sin, cos, pi height = int(sys.argv[1]) width = height / 4 * 3 turtle.screensize(width, height) t = turtle.Turtle() # the layout t.pencolor("#0044cc") t.fillcolor("#cc2244") t.pensize(width / 25) t.pendown() t.fill(True) t.forward(width) t.left(135) t.forward(width) t.right(135) t.forward(width / sqrt(2)) t.right(90) t.goto(0, height) t.forward(height) t.fill(False) t.penup() # the bottom star t.fillcolor("#ffffff") t.pencolor("#ffffff") t.pensize(1) radius = width / 5 x = width / 4 y = height / 4 t.goto(x + radius, y) t.pendown() t.fill(True) for i in range(24): t.goto(x + radius * (5 + (-1) ** i) / 6 * cos(i * pi / 12), y + radius * (5 + (-1) ** i) / 6 * sin(i * pi / 12)) t.fill(False) t.penup() # the top star radius = width / 9 x = width / 4 y = height * 2 / 3 t.goto(x + radius, y) t.pendown() t.fill(True) for i in range(28): t.goto(x + radius * (6 + (-1) ** i) / 7 * cos(i * pi / 14), y + radius * (6 + (-1) ** i) / 7 * sin(i * pi / 14)) t.fill(False) t.penup() # the moon radius = width / 5 x = width / 4 y = height / sqrt(2) t.goto(x + radius, y) t.pendown() t.fill(True) for i in range(30): t.goto(x + radius * cos(i * pi / 30), y - radius * sin(i * pi / 30)) for i in range(30): t.goto(x - radius * cos(i * pi / 30), y - radius / 2 * sin(i * pi / 30)) t.fill(False) t.penup() t.hideturtle() raw_input("press enter") 

Uses python's Tk turtles, example of python nepal.py 150 and python nepal.py 200 respectively:

Python (+PIL), 578

Because I'm quite bored today..

from PIL import Image,ImageDraw from math import* I,k,l,m,n,o,_=Image.new('P',(394,480)),479,180,465,232,347,255;D=ImageDraw.Draw(I);P,G=D.polygon,D.pieslice I.putpalette([_,_,_,0,0,_,_,20,60]) def S(x,y,r,e,l,b): p,a,h=[],2*pi/e,r*l;c,d=[0,-a/2][b],[a/2,0][b] for i in range(e):p+=[(x+r*cos(i*a+c),y+r*sin(i*a+c)),(x+h*cos(i*a+d),y+h*sin(i*a+d))] P(p,fill=0) P([(0,0),(393,246),(144,246),(375,k),(0,k)],fill=1) P([(14,25),(o,n),(110,n),(o,m),(14,m)],fill=2) S(96,o,68,12,.6,0) G([(31,90),(163,221)],0,l,fill=0) G([(28,68),(166,200)],0,l,fill=2) S(96,178,40,16,.7,1) I.show() 

PostScript

Code:

.15 .15 scale % over-all scale % draw the red area and blue border 7 7 moveto 360 7 lineto 128 240 lineto 367 240 lineto 7 467 lineto closepath gsave % save the outline path for further use .86 .08 .24 setrgbcolor % crimson red fill % draw the red area grestore % get back the saved outline path 0 .22 .58 setrgbcolor % dark blue 14 setlinewidth stroke % draw the blue border 1 setgray % white % draw the lower sun 96 130 translate % coordinate origin of sun 69 0 moveto 12 { % 12 spikes 69 0 lineto 15 rotate 46 0 lineto 15 rotate } repeat closepath fill % draw the upper sun 0 167 translate % coordinate origin at center of sun 29 0 moveto 16 { % 16 spikes 29 0 lineto 11.25 rotate 42 0 lineto 11.25 rotate } repeat closepath fill % draw the crescent moon 0 24 65 180 0 arc % the lower arc 0 57 72 335 205 arcn % the upper arc closepath fill showpage 

The flag size can be controlled by specifying the resolution in the Ghostscript call.

Result (height of flag is 480 pixels, created by gswin64c -r480 nepal.ps):

Result (height of flag is 120 pixels, created by gswin64c -r120 nepal.ps):