39
\$\begingroup\$

Not to be confused with Find the factorial!

Introduction

The factorial of an integer n can be calculated by $$n!=n\times(n-1)\times(n-2)\times(...)\times2\times1$$

This is relatively easy and nothing new. However, factorials can be extended to double factorials, such that $$n!!=n\times(n-2)\times(n-4)\times(...)\times4\times2$$ for even numbers, and $$n!!=n\times(n-2)\times(n-4)\times(...)\times3\times1$$ for odd numbers. But we're not limited to double factorials. For example $$n!!!=n\times(n-3)\times(n-6)\times(...)\times6\times3$$ or $$n!!!=n\times(n-3)\times(n-6)\times(...)\times5\times2$$ or $$n!!!=n\times(n-3)\times(n-6)\times(...)\times4\times1$$ depending on the starting value.

In summary: $${\displaystyle n!^{(k)}={\begin{cases}1&{\text{if }}n=0 \\n&{\text{if }}0<n\leq k\\n\cdot\left({(n-k)!}^{(k)}\right)&{\text{if }}n>k\end{cases}}}$$ where $${\displaystyle n!^{(k)}=n\underbrace{!\dots!}_{k}}$$ Or, in plain English: Subtract the factorial count from the base number repeatedly and multiply all resulting positive integers.

The Challenge

Write a function that will calculate any kind of repeated factorial for any non-negative integer.

Input

Either

  • A string containing a non-negative base-ten integer, followed by 1 or more exclamation marks. E.g. "6!" or "9!!" or "40!!!!!!!!!!!!!!!!!!!!".

or

  • The same values represented by two integers: one non-negative base value and one positive value representing the factorial count. This can be done according to any format from the default I/O rules.

Output

The result of said calculation.

Challenge remarks

  • 0! equals 1 by definition. Your code must account for this.
  • The factorial count is limited by $$ 0 < factorial~count \leq base~value $$outside this range, you are free to output whatever. Aside from 0!, which is the only exception to this rule.

Examples

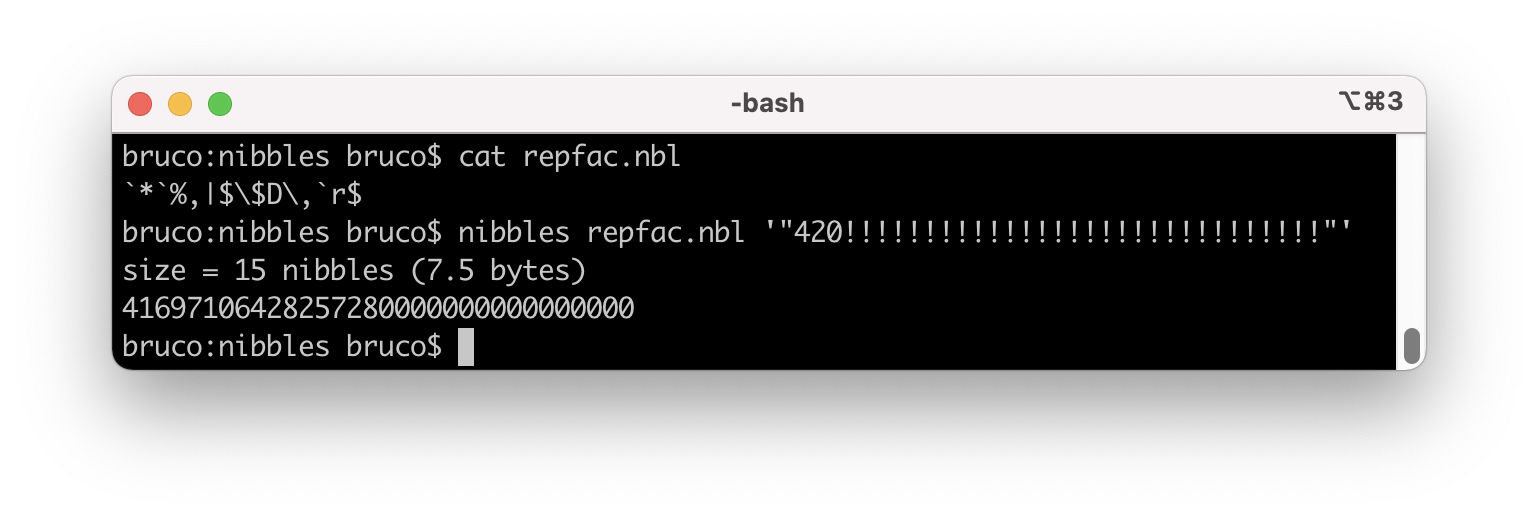
Input Output 3!!! 3 0! 1 6! 720 9!! 945 10!!!!!!!! 20 40!!!!!!!!!!!!!!!!!!!! 800 420!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 41697106428257280000000000000000

Try it with an ungolfed Python implementation: Try it online!

General remarks

Improve this question
\$\endgroup\$
8
  • 7
    \$\begingroup\$ The examples list 0! but the challenge remarks say that the factorial count will be less than or equal to the base value. \$\endgroup\$ Commented Aug 5, 2019 at 13:09
  • 1
    \$\begingroup\$ Wouldn't 3!!! be zero? n*(n-3) = 3*(3-3) = 0. \$\endgroup\$ Commented Aug 5, 2019 at 13:31
  • 2
    \$\begingroup\$ @ouflak If it works like 1!, not really. It's more like 1! = 1. 2!! = 2. 3!!! = 3. There's no calculation, because you are at the end of the recursiveness. No 0 in products or else every single factorial would drop down to 0 in the end. \$\endgroup\$ Commented Aug 5, 2019 at 14:16
  • 4
    \$\begingroup\$ 3!!!!!!! should not be undefined—it should just yield the answer 3. It's the same as 1!!=1 (not undefined). Also your input specification says that there will always be at least one !, so the first example 3 doesn't fit the specification. \$\endgroup\$ Commented Aug 5, 2019 at 18:04
  • 4
    \$\begingroup\$ @FabianRöling: But that's not what this is. It's not (3!)! instead it's removing terms from a factorial. It's a misleading name; I came in assuming it was going to be applying the Factorial function repeatedly in a chain and had to read carefully to see what it actually was. Fortunately the question does explain it clearly. A better name might be stride factorial or step factorial or something. \$\endgroup\$ Commented Aug 8, 2019 at 5:31

42 Answers 42

Reset to default
1
2
17
\$\begingroup\$

R, 33 bytes

function(n,k)prod(seq(n+!n,1,-k))

Try it online!

Handles \$n=0\$ by adding the logical negation of \$n\$.

Improve this answer
\$\endgroup\$
14
\$\begingroup\$

ArnoldC, 702 698 634 bytes

LISTEN TO ME VERY CAREFULLY f I NEED YOUR CLOTHES YOUR BOOTS AND YOUR MOTORCYCLE n I NEED YOUR CLOTHES YOUR BOOTS AND YOUR MOTORCYCLE p GIVE THESE PEOPLE AIR HEY CHRISTMAS TREE r YOU SET US UP 1 HEY CHRISTMAS TREE c YOU SET US UP 0 STICK AROUND n GET TO THE CHOPPER r HERE IS MY INVITATION r YOU'RE FIRED n ENOUGH TALK GET TO THE CHOPPER n HERE IS MY INVITATION n GET DOWN p ENOUGH TALK GET TO THE CHOPPER c HERE IS MY INVITATION 0 LET OFF SOME STEAM BENNET n ENOUGH TALK BECAUSE I'M GOING TO SAY PLEASE c GET TO THE CHOPPER n HERE IS MY INVITATION 0 ENOUGH TALK YOU HAVE NO RESPECT FOR LOGIC CHILL I'LL BE BACK r HASTA LA VISTA, BABY

Try it online!

Translated to pseudocode:

f(n,p) { r=1; c=0; while (n) { r=r*n; n=n-p; c=n<0; if (c) n=0; } return r; }

Note: ArnoldC has only one type of data: 16-bit signed integer. Hence I cannot test the 420!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! case.

Improve this answer
\$\endgroup\$
3
  • \$\begingroup\$ Just curious about your psuedocode. What is the variable 'c' for? \$\endgroup\$ Commented Aug 6, 2019 at 16:28
  • \$\begingroup\$ @ouflak I edited my answer a couple of times and forgot it. The c variable actually stores the value of the comparison between n and 0. \$\endgroup\$ Commented Aug 6, 2019 at 16:40
  • \$\begingroup\$ +1 and I borrowed it (minus the 'c') for my LUA answer. \$\endgroup\$ Commented Aug 6, 2019 at 16:42
13
\$\begingroup\$

Jelly, 4 bytes

RṚmP

Try it online!

How? Given \$n\$ and \$k\$, it first generates the range \$n,\cdots, 1\$ (with RṚ), then with m it keeps every \$k^{\text{th}}\$ element of this range (so \$n, n-k, n-2k,\cdots,n-\lfloor n/k\rfloor k\$), and finally multiplies them using P.

Improve this answer
\$\endgroup\$
8
  • \$\begingroup\$ Works well, and so simple in the end. I don't know Jelly at all but at least it looks good :) \$\endgroup\$ Commented Aug 5, 2019 at 14:20
  • 1
    \$\begingroup\$ @V.Courtois Given \$n\$ and \$k\$, it first generates the range \$n,\cdots, 1\$ (with RṚ), then with m it keeps every \$k^{\text{th}}\$ element of this range (so \$n, n-k, n-2k,\cdots,n-\lfloor n/k\rfloor k\$), and finally multiplies them using P. Just the straightforward approach. Edit: I added this explanation in the answer. \$\endgroup\$ Commented Aug 5, 2019 at 14:38
  • \$\begingroup\$ Hah thank you very much. One day I might want to golf in this language so I'll have to learn those monads, dyads etc. \$\endgroup\$ Commented Aug 5, 2019 at 14:58
  • \$\begingroup\$ Alternative that looks like CJam: r1mP. \$\endgroup\$ Commented Aug 5, 2019 at 18:07
  • 1
    \$\begingroup\$ @KyeWShi Jelly has its own codepage, so each of the 256 characters it contains is encoded as 1 byte. \$\endgroup\$ Commented Aug 7, 2019 at 13:41
8
\$\begingroup\$

APL (Dyalog Extended), 7 bytesSBCS

Anonymous tacit prefix function. Takes [n,b] as argument.

×/-\…1¨

Try it online!

1¨ one for each element of the argument; [1,1]

-\ cumulative difference; [n,n-b]

… range using second element of left argument as indicator of step, e.g. [9,7] continues with 5

×/ product

Improve this answer
\$\endgroup\$
8
\$\begingroup\$

Haskell, 21 bytes

n%a=product[n,n-a..1]

Try it online!

Combining the built-in product function with stepped range enumeration beats what I could code up recursively (even with flawr saving a byte).

22 bytes

n%a|n<1=1|m<-n-a=n*m%a

Try it online!

Here's a solution taking input in string format like 9!!, which I think is more interesting.

42 bytes

(\[(n,a)]->product[n,n-length a..1]).reads

Try it online!

Improve this answer
\$\endgroup\$
1
  • 3
    \$\begingroup\$ I think you could shorten the recursive solution to n%a|n<1=1|m<-n-a=n*m%a \$\endgroup\$ Commented Aug 5, 2019 at 8:41
6
\$\begingroup\$

Pyth, 6 bytes

These are all equivalent 6-byters:

*F:Q1E *F:E1Q *F%E_S

Try it online! (*F:Q1E)

Or, 11 bytes, taking input as a string:

*F:.vQ1/Q\!

Test suite.

Improve this answer
\$\endgroup\$
5
\$\begingroup\$

JavaScript (ES6), 21 bytes

Takes input as (k)(n).

k=>g=n=>n<1||n*g(n-k)

Try it online!

Or 24 bytes to support BigInts.

JavaScript (ES6), 55 bytes

Takes input as a string, using the format described in the challenge.

s=>(a=s.split`!`,k=a.length-1,g=n=>n<1||n*g(n-k))(a[0])

Try it online!

Improve this answer
\$\endgroup\$
0
5
\$\begingroup\$

Whitespace, 91 bytes

[S S S T N Push_1][S N S _Duplicate_1][S N S _Duplicate_1][T N T T _Read_STDIN_as_integer_(base)][T T T _Retrieve_base][S S S N _Push_0][T N T T _Read_STDIN_as_integer_(factorial)][N S S N _Create_Label_LOOP][S N S _Duplicate_base][S S S T N _Push_1][T S S T _Subtract][N T T S N _If_negative_jump_to_Label_PRINT_RESULT][S N S _Duplicate_base][S T S S T S N _Copy_0-based_2nd_(result)][T S S N _Multiply][S N T _Swap_top_two][S S S N _Push_0][T T T _Retrieve_factorial][T S S T _Subtract][N S N N _Jump_to_Label_LOOP][N S S S N _Create_Label_PRINT_RESULT][S N N _Discard_top][T N S T _Print_result_as_integer]

Letters S (space), T (tab), and N (new-line) added as highlighting only.
[..._some_action] added as explanation only.

Try it online (with raw spaces, tabs and new-lines only).

Explanation in pseudo-code:

Integer result = 1 Integer base = STDIN as integer Integer factorial = STDIN as integer Start LOOP: If(base <= 0): Call function PRINT_RESULT result = result * base base = base - factorial Go to next iteration of LOOP function PRINT_RESULT: Print result as integer to STDOUT
Improve this answer
\$\endgroup\$
5
\$\begingroup\$

Python 2, 29 bytes

f=lambda n,b:n<1or n*f(n-b,b)

Try it online!

Improve this answer
\$\endgroup\$
5
\$\begingroup\$

05AB1E, 10 8 7 bytes

ݦRIιнP

Input as two separated inputs: first input being base; second input being factorial.

Try it online or verify all test cases.

-2 bytes thanks to @Mr.Xcoder.
-1 byte thanks to @JonathanAllan.

Explanation:

Ý # Create a list in the range [0, (implicit) base-input] ¦ # And remove the first item to make it the range [1, base] # (NOTE: this is for the edge case 0. For the other test cases simply `L` instead # of `ݦ` is enough.) R # Reverse this list so the range is [base, 1] Iι # Uninterleave with the second input as step-size # i.e. base=3, factorial=7: [[3],[2],[1],[],[],[],[]] # i.e. base=10, factorial=8: [[10,2],[9,1],[8],[7],[6],[5],[4],[3]] # i.e. base=420, factorial=30: [[420,390,360,...,90,60,30],[419,389,359,...],...] н # Only leave the first inner list P # And take the product of its values # (which is output implicitly as result)

Original 10 bytes answer:

L0KD¤-IÖÏP

Input as two separated inputs: first input being base; second input being factorial.

Try it online or verify all test cases.

Explanation:

L # Create a list in the range [1, (implicit) base-input] 0K # Remove all 0s (edge case for input 0, which will become the list [1,0]) D # Duplicate this list ¤ # Get the last value (without popping) # (could also be `Z` or `¹` for max_without_popping / first input respectively) - # Subtract it from each item in the list IÖ # Check for each if they're divisible by the second factorial-input Ï # In the list we copied, only leave the values at the truthy indices P # And take the product of those # (which is output implicitly as result)
Improve this answer
\$\endgroup\$
9
  • 1
    \$\begingroup\$ This 6-byter: LR²ιнP (Try it online!) works for every test case, except for 0. \$\endgroup\$ Commented Aug 5, 2019 at 8:20
  • \$\begingroup\$ But I guess that 0 case can be fixed in at most 2 bytes. If you figure out a way to fix it, you may take it :) EDIT: Perhaps LR²ιн0KP for 8 bytes? \$\endgroup\$ Commented Aug 5, 2019 at 8:20
  • \$\begingroup\$ @Mr.Xcoder Nice answer! Never even used uninterleave with a given step. :) \$\endgroup\$ Commented Aug 5, 2019 at 8:29
  • \$\begingroup\$ 0K should be unnecessary as 0! is an invalid input by the specification (even though it's been included in the examples) - I have commented about this. \$\endgroup\$ Commented Aug 5, 2019 at 19:10
  • 1
    \$\begingroup\$ ...and if 0! is in the input domain ݦRXιнP saves a byte. \$\endgroup\$ Commented Aug 5, 2019 at 19:15
4
\$\begingroup\$

Perl 6, 22 bytes

{[*] $^a,*-$^b...^1>*}

Try it online!

Anonymous codeblock that returns the product of the range starting from the first input, decreasing by the second until it is below 1, excluding the last number. This works for 0, since the base case of a the reduce by product is 1, so the output is 1.

Improve this answer
\$\endgroup\$
4
\$\begingroup\$

x86-64 machine code, 12 bytes

Same machine code does the same thing in 32-bit mode, and for 16-bit integers in 16-bit mode.

This is a function, callable with args n=RCX, k=ESI. 32-bit return value in EAX.

Callable from C with the x86-64 System V calling convention with dummy args to get the real args into the right registers. uint32_t factk(int, uint32_t k, int, uint64_t n); I couldn't just use Windows x64 because 1-operand mul clobbers RDX, and we don't want REX prefixes to access R8/R9. n must not have any garbage in the high 32 bits so JRCXZ works, but other than that it's all 32-bit.

NASM listing (relative address, machine code, source)

 1 factk: 2 00000000 6A01 push 1 3 00000002 58 pop rax ; retval = 1 4 00000003 E306 jrcxz .n_zero ; if (n==0) return 5 .loop: ; do { 6 00000005 F7E1 mul ecx ; retval *= n (clobbering RDX) 7 00000007 29F1 sub ecx, esi ; n -= k 8 00000009 77FA ja .loop ; }while(sub didn't wrap or give zero) 9 .n_zero: 10 0000000B C3 ret

0xc = 12 bytes

Or 10 bytes if we didn't need to handle the n=0 special case, leaving out the jrcxz.

For standard factorial you'd use loop instead of sub/ja to save 2 bytes, but otherwise the exact same code.

Test caller that passes argc as k, with n hard-coded.

align 16 global _start _start: mov esi, [rsp] ;main: mov ecx, 9 call factk mov esi, eax mov edx, eax lea rdi, [rel print_format] xor eax, eax extern printf call printf extern exit call exit section .rodata print_format: db `%#x\t%u\n` ```
Improve this answer
\$\endgroup\$
3
\$\begingroup\$

APL (Dyalog Unicode), 11 bytesSBCS

Anonymous tacit infix function. Takes n as right argument and b as left argument.

×/1⌈⊢,⊢-×∘⍳

Try it online!

×∘⍳ multiply b by the ɩntegers 1 through n

⊢- subtract that from n

⊢, prepend n

1⌈ max of one and each of those

×/ product

Improve this answer
\$\endgroup\$
3
\$\begingroup\$

Ruby, 25 bytes

f=->s,r{s<1?1:s*f[s-r,r]}

Try it online!

Improve this answer
\$\endgroup\$
3
\$\begingroup\$

Wolfram Language (Mathematica), 22 21 bytes

1##&@@Range[#,1,-#2]&

Try it online!

-1 thanks to attinat: Times --> 1##&

Explanation: use Range to make a list of the values {n, n-k, n-2k, n-3k, ...}, stopping before going below 1 (i.e., stopping just right). Then multiply all numbers in this list with Times (or 1##&).

Improve this answer
\$\endgroup\$
1
  • \$\begingroup\$ -1 byte with 1##& instead of Times \$\endgroup\$ Commented Aug 5, 2019 at 17:49
3
\$\begingroup\$

Java 10, 44 bytes

f->b->{int r=1;for(;b>0;b-=f)r*=b;return r;}

Takes the factorial as first input, base as second.

Try it online.

This above doesn't work for the largest test case due to the limited integer range (32-bits). To fix this we can use BigIntegers, which coincidentally is exactly double the size - 88 79 bytes:

f->b->{var r=f.ONE;for(;b.signum()>0;b=b.subtract(f))r=r.multiply(b);return r;}

-9 bytes thanks to @OlivierGrégoire.

Try it online.

Explanation:

f->b->{ // Method with two integer parameters and integer return-type int r=1; // Result-integer, starting at 1 for(;b>0; // Loop as long as the base is still larger than 0 b-=f) // After every iteration: decrease the base by the factorial r*=b; // Multiply the result by the base return r;} // Return the result
Improve this answer
\$\endgroup\$
2
3
\$\begingroup\$

Vyxal, 4 bytes

ɾṘḞΠ

Try it Online!

Improve this answer
\$\endgroup\$
3
\$\begingroup\$

Knight, 34 33 bytes

;=p=xE P;=yP;W<0=x-x y=p*x pO+p!p

Try it online!

-1 byte thanks to Aiden Chow

Improve this answer
\$\endgroup\$
3
  • \$\begingroup\$ 33 bytes: ;=pT;=xP;=yP;W<0x;=p*x p=x-Ex yOp. \$\endgroup\$ Commented Aug 17, 2022 at 2:33
  • \$\begingroup\$ @AidenChow I tried that initially. That doesn't work for 0! as it will output true instead. \$\endgroup\$ Commented Aug 17, 2022 at 3:20
  • \$\begingroup\$ Oops didn't test it lol. What about this? ;=p=xE P;=yP;W<0=x-x y=p*x pO+p!p \$\endgroup\$ Commented Aug 17, 2022 at 6:14
2
\$\begingroup\$

Japt, 8 bytes

TõUV f ×

Try it

-1 thanks to EoI pointing out how dumb uncaffeinated Shaggy can be!

Improve this answer
\$\endgroup\$
2
  • \$\begingroup\$ kT can be replaced with f for 1 byte \$\endgroup\$ Commented Aug 5, 2019 at 9:47
  • 1
    \$\begingroup\$ @EmbodimentofIgnorance, of course it can! I knew it was too early for golf! :\ \$\endgroup\$ Commented Aug 5, 2019 at 9:48
2
\$\begingroup\$

C (gcc), 41 bytes

r;f(n,k){for(r=1;n>0;n-=k)r*=n;return r;}

Try it online!

Improve this answer
\$\endgroup\$
1
  • \$\begingroup\$ 36 bytes r;f(n,k){for(r=1;n>0;n-=k)r*=n;n=r;} for C(gcc) \$\endgroup\$ Commented Aug 8, 2019 at 9:48
2
\$\begingroup\$

MathGolf, 7 6 bytes

╙╒x%ε*

Try it online!

Found a clever way to handle 0! without changing the other test cases. Takes input as k n (reverse order), which helps with implicit popping.

Explanation

╙ maximum of two elements (pops largest of k and n, which is n for every valid case except 0!, where 1 is pushed) ╒ range(1,n+1) x reverse int/array/string % slice every k:th element ε* reduce list with multiplication
Improve this answer
\$\endgroup\$
2
\$\begingroup\$

Attache, 21 19 bytes

${x<y∨x*$[x-y,y]}

Try it online! Pretty direct recursive implementation. (Note: true is essentially 1, as it can be used in arithmetic operations as 1.) This is one of the few programs I've written for this site where using a unicode operator saves bytes (1, to be precise).

Alternatives

20 bytes: ${x<y or x*$[x-y,y]}

21 bytes: Prod@${{_%y=x%y}\1:x}

27 bytes: ${x*[`1,$][x>y][x-y,y]∨1}

27 bytes: ${If[x>y,x*$[x-y,y],_or 1]}

27 bytes: ${x*[`1,$][x>y][x-y,y]or 1}

29 bytes: ${If[x>y,x*$[x-y,y],_+not _]}

Improve this answer
\$\endgroup\$
2
\$\begingroup\$

Scala, 53 bytes

Takes two arguments, the first being the number and the second being the ! count.
Somehow breaks on the big test case. This step range costs many bytes in the end because of this -1* so improvements ought to be possible by refactoring.
I have, as always, a doubt about how we count bytes for function declarations, because everyone doesn't do the same way everywhere down there, so well... It's 17 bytes less, so 36 bytes, if we count out func variables' (a and b) declaration and func brackets.

(a:Int,b:Int)=>{var s=1 for(i<-a to b by -1*b)s*=i s}

Try it online! I commented out the broken test cases, because, well, they do break.

Improve this answer
\$\endgroup\$
2
  • \$\begingroup\$ You need the function declaration, otherwise this would be a snippet that takes input via predefined variables. Typically only the function assignment is left out since anonymous functions are allowed as submissions, though it depends on the language and the question \$\endgroup\$ Commented Aug 6, 2019 at 6:57
  • \$\begingroup\$ Ok thanks, so it is 53 indeed. \$\endgroup\$ Commented Aug 6, 2019 at 7:00
2
\$\begingroup\$

Rust, 92 73 61 bytes

fn f(n:i128,k:i128)->i128{if n<=0{return 1}return n*f(n-k,k)}

I am just starting to learn rust, so I'm sure this can be shorter. Will update as I learn. The return value should be i128 in order to compute the last test.

Edit: Recursion is shorter.

Try it online!

You can add your own test, or edit one of the already existing ones.

Improve this answer
\$\endgroup\$
2
\$\begingroup\$

q, 59 57 55 53 bytes

{prd 2+(&)1_i=last i:("J"$x(&)not[n])#(!)sum n:"!"=x}

explanation:

q)x:"12!!" / let our input be 12!!, assign to x q)sum n:"!"=x / count "!"s 2i q)(!)sum n:"!"=x / (!)m -> [0,m) 0 1 q)("J"$x(&)not[n]) / isolate the number in input 12 q)("J"$x(&)not[n])#(!)sum n:"!"=x / x#y means take x items from list y, if x>y, circle around 0 1 0 1 0 1 0 1 0 1 0 1 q)i:("J"$x(&)not[n])#(!)sum n:"!"=x / assign to i q)i 0 1 0 1 0 1 0 1 0 1 0 1 q)(last i)=i:("J"$x(&)not[n])#(!)sum n:"!"=x / take last elem of i and see which are equal in i 010101010101b q)1_(last i)=i:("J"$x(&)not[n])#(!)sum n:"!"=x / drop first elem 10101010101b q)(&)1_(last i)=i:("J"$x(&)not[n])#(!)sum n:"!"=x / indices of 1b (boolean TRUE) 0 2 4 6 8 10 q)2+(&)1_(last i)=i:("J"$x(&)not[n])#(!)sum n:"!"=x / add 2 across array 2 4 6 8 10 12 q)prd 2+(&)1_(last i)=i:("J"$x(&)not[n])#(!)sum n:"!"=x / product across array 46080

here also is a version in k (same logic), 4241 bytes

{*/2+&1_i=last i:("J"$x@&~:n)#!+/n:"!"=x}
Improve this answer
\$\endgroup\$
6
  • \$\begingroup\$ Welcome to the site! I've added code formatting to your post which can be done with four spaces before the line or by enclosing it with triple backticks. \$\endgroup\$ Commented Aug 9, 2019 at 13:51
  • \$\begingroup\$ @SriotchilismO'Zaic thanks :-) \$\endgroup\$ Commented Aug 9, 2019 at 14:30
  • 1
    \$\begingroup\$ I recommend adding an explanation and maybe a link to an online interpreter like TIO. Code-only answers are usually automatically flagged as low quality. \$\endgroup\$ Commented Aug 9, 2019 at 14:45
  • \$\begingroup\$ @mbomb007 interesting. is there a bot flagging answers? what happens to low-quality submissions? i will update soon! \$\endgroup\$ Commented Aug 9, 2019 at 15:09
  • \$\begingroup\$ Yes, there is a bot. StackExchange uses bots to look for potential spam and low quality answers. People with high enough reputation can view the Review Queue. meta.stackexchange.com/a/161391/285610 \$\endgroup\$ Commented Aug 9, 2019 at 15:40
2
+400
\$\begingroup\$

Factor + math.unicode, 30 29 24 bytes

  • Saved 1 byte thanks to @Bubbler
  • Saved 5 bytes thanks to @chunes!
[ 1 rot neg <range> Π ]

Try it online!

Takes k (which -th factorial) and then n. First we push an n onto the stack, then rot makes the stack look like n 1 k. neg negates k, which will act as the step for a range from n to 1 (made using <range>). Then Π finds the product of that range, and that's it.

Improve this answer
\$\endgroup\$
2
  • 1
    \$\begingroup\$ If you take the arguments in k n order, you can do 1 rot neg instead of neg 1 swap to save a byte. \$\endgroup\$ Commented Mar 29, 2021 at 23:19
  • 1
    \$\begingroup\$ You can save 5 bytes with Π from math.unicode instead of product. \$\endgroup\$ Commented Mar 30, 2021 at 0:26
2
\$\begingroup\$

Nibbles, 3.5 bytes (7 nibbles)

`*`%@\, 
 , # get the range from 1..first input, \ # reverse it, % # and take each element in steps of @ # the second input, `* # and finally get the product

enter image description here

Or 7.5 bytes (15 nibbles) with input as string of a base-ten integer followed by exclamation marks:

`*`%,|$\$D\,`r$

enter image description here

Improve this answer
\$\endgroup\$
1
\$\begingroup\$

Physica, 22 bytes

f=>n;k:n<1||n*f[n-k;k]

Try it online!

26 bytes

Re-learning how to use my own "language" \o/... If I knew how to write a parser 2 years ago, this would have been 20 bytes :(

->n;k:GenMul##[n…1]{%%k}

or

->n;k:GenMul##Range[n;1;k]

Try it online!

Improve this answer
\$\endgroup\$
1
\$\begingroup\$

Retina, 66 bytes

^0 1 \d+ *!, +`(!+)(!+),\1$ $1$2,$2,$1 !+$ 1 +`(!+),(\d+) $.($2*$1

Try it online! Link includes faster test cases. Mauls numbers without exclamation marks. Explanation:

^0 1

Fix up 0!.

\d+ *!,

Convert n to unary and add a separator.

+`(!+)(!+),\1$ $1$2,$2,$1

Repeatedly subtract k from n while n>k, and collect the results.

!+$ 1

Replace k with 1 (in decimal).

+`(!+),(\d+) $.($2*$1

Multiply by each intermediate value in turn, converting to decimal.

Improve this answer
\$\endgroup\$
1
\$\begingroup\$

Japt, 8 bytes

1õUV f ×

Try it

Improve this answer
\$\endgroup\$
1
2

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.