C 127 119 116 108 65
This one uses the trick of the HTML answer of ^ i & j getting it to print pretty output would take 1 more char (you can get really ugly output by sacrificing the a^).
a=32,j;main(i){for(;++i<a;)putchar(a^i&j);++j<a&&main(puts(""));}
To make it pretty turn (32^i&j) to (32|!(i&j)) and turn it from ++i<a to ++i<=a. However wasting chars on looks seems ungolfish to me.
Ugly output:
! ! ! ! ! ! ! ! ! ! ! ! ! ! ! "" "" "" "" "" "" "" "" "# !"# !"# !"# !"# !"# !"# !"# $$$$ $$$$ $$$$ $$$$ !$%$% ! !$%$% ! !$%$% ! !$%$% ""$$&& ""$$&& ""$$&& ""$$&& "#$%&' !"#$%&' !"#$%&' !"#$%&' (((((((( (((((((( ! ! !()()()() ! ! ! !()()()() "" ""((**((** "" ""((**((** "# !"#()*+()*+ !"# !"#()*+()*+ $$$$((((,,,, $$$$((((,,,, !$%$%()(),-,- ! !$%$%()(),-,- ""$$&&((**,,.. ""$$&&((**,,.. "#$%&'()*+,-./ !"#$%&'()*+,-./ 0000000000000000 ! ! ! ! ! ! !0101010101010101 "" "" "" ""0022002200220022 "# !"# !"# !"#0123012301230123 $$$$ $$$$0000444400004444 !$%$% ! !$%$%0101454501014545 ""$$&& ""$$&&0022446600224466 "#$%&' !"#$%&'0123456701234567 ((((((((0000000088888888 ! ! !()()()()0101010189898989 "" ""((**((**0022002288::88:: "# !"#()*+()*+0123012389:;89:; $$$$((((,,,,000044448888<<<< !$%$%()(),-,-010145458989<=<= ""$$&&((**,,..0022446688::<<>> "#$%&'()*+,-./0123456789:;<=>?
I actually kind of like how it looks. But if you insist on it being pretty you can dock four chars. Pretty Output:
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! !! !! !! !! !! !! !! ! ! ! ! ! ! ! ! ! !! !!!! !!!! !!!! ! ! ! ! ! ! ! ! ! !! !! !! ! ! ! ! ! !!!!!! !!!!!!!! ! ! ! ! ! ! ! ! ! !! !! !! ! ! ! ! ! !! !!!! ! ! ! ! ! !! ! ! ! !!!!!!!!!!!!!! ! ! ! ! ! ! ! ! ! !! !! !! ! ! ! ! ! !! !!!! ! ! ! ! ! !! ! ! ! !!!!!! ! ! ! ! ! !! ! ! ! !! ! ! ! ! !
Leaving up the older 108 char, cellular automata version.
j,d[99][99];main(i){d[0][31]=3;for(;i<64;)d[j+1][i]=putchar(32|d[j][i+2]^d[j][i++]);++j<32&&main(puts(""));}
So I don't think I'm going to get it much shorter than this so I'll explain the code. I'll leave this explanation up, as some of the tricks could be useful.
j,d[99][99]; // these init as 0 main(i){ //starts at 1 (argc) d[0][48]=3; //seed the automata (3 gives us # instead of !) for(;i<98;) // print a row d[j+1][i]=putchar(32|d[j][i+2]]^d[j][i++]); //relies on undefined behavoir. Works on ubuntu with gcc ix864 //does the automata rule. 32 + (bitwise or can serve as + if you know //that (a|b)==(a^b)), putchar returns the char it prints ++j<32&&main(puts("")); // repeat 32 times // puts("") prints a newline and returns 1, which is nice }
Some output
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #






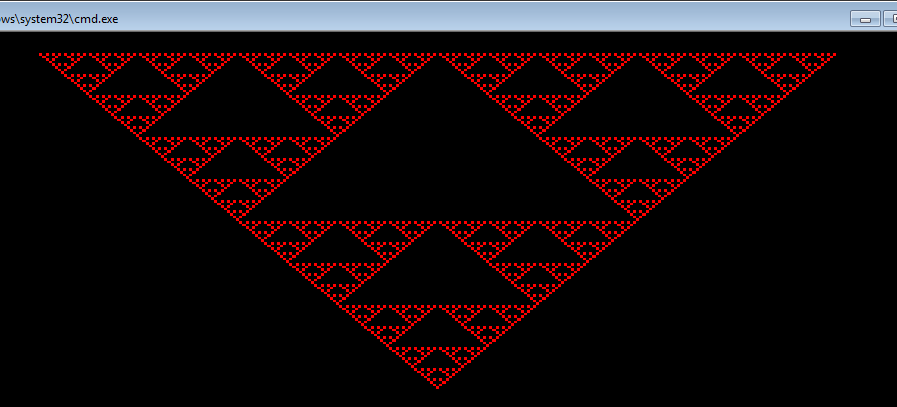

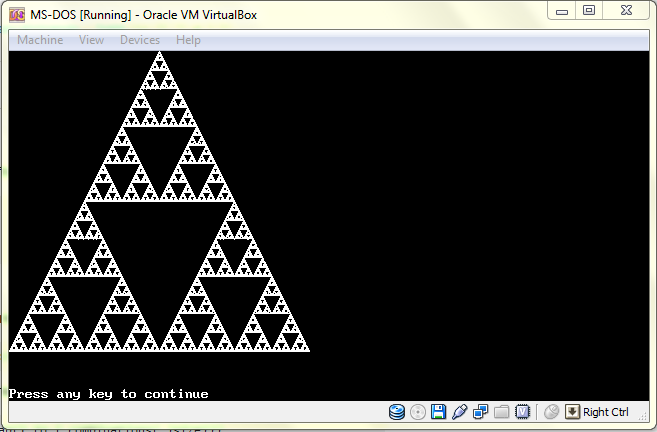
 :D
:D
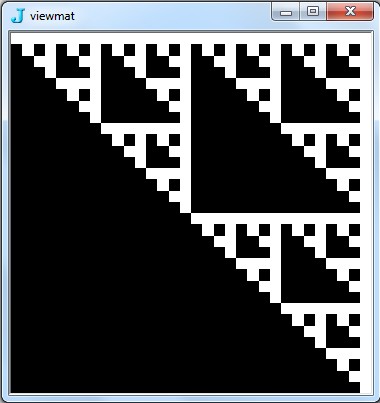

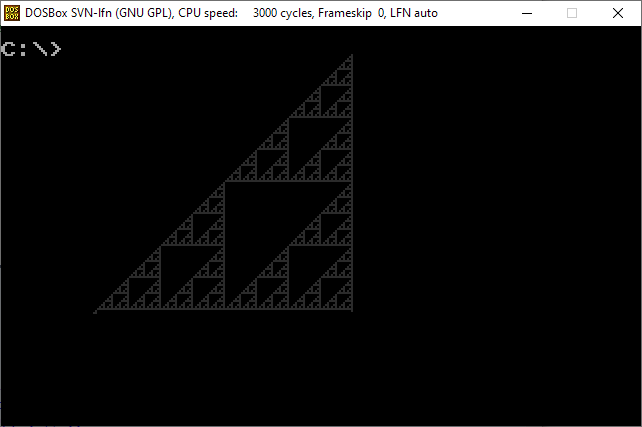
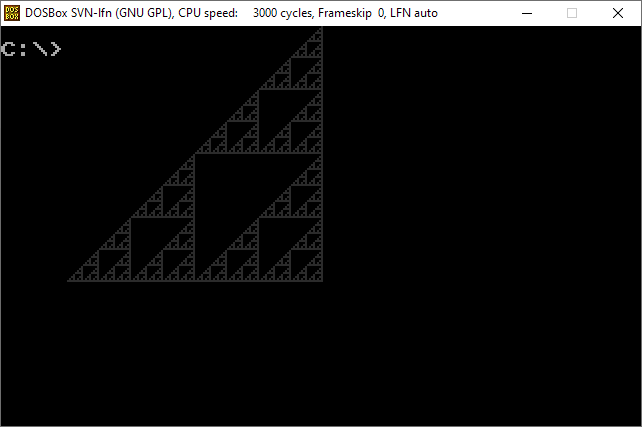






![Image@Array[BitAnd,{2,2}^9,0]](https://i.sstatic.net/7IR6g.jpg)
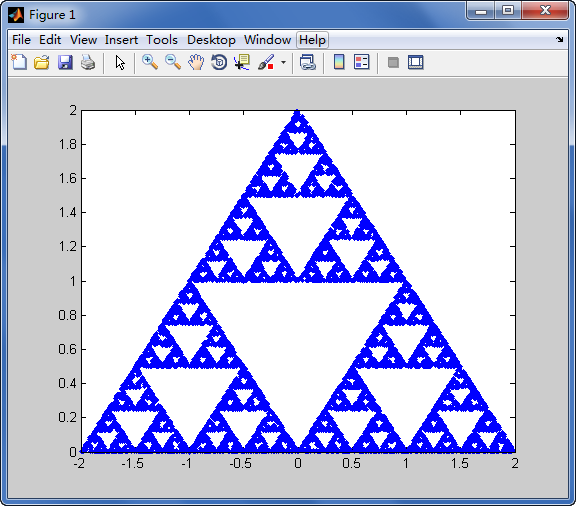
![Image3D[1-Array[BitXor,{2,2,2}^7,0]]](https://i.sstatic.net/TUzsq.jpg)