I have spent about more than a year in python, but I come from biology background. I should say I have got some understanding of for-loop and nested-for-loop to workout the solution to the problem I have had. But, I suppose that there are better and comprehensive way of solving problem.
Below is the code I wrote to solve the haplotype phase state between two haplotype blocks.
Here is a short snipped of my data:
chr pos ms01e_PI ms01e_PG_al ms02g_PI ms02g_PG_al ms03g_PI ms03g_PG_al ms04h_PI ms04h_PG_al ms05h_PI ms05h_PG_al ms06h_PI ms06h_PG_al 2 15881764 4 C|T 6 C|T 7 T|T 7 T|T 7 C|T 7 C|T 2 15881767 4 C|C 6 T|C 7 C|C 7 C|C 7 T|C 7 C|C 2 15881989 4 C|C 6 A|C 7 C|C 7 C|C 7 A|T 7 A|C 2 15882091 4 G|T 6 G|T 7 T|A 7 A|A 7 A|T 7 A|C 2 15882451 4 C|T 4 T|C 7 T|T 7 T|T 7 C|T 7 C|A 2 15882454 4 C|T 4 T|C 7 T|T 7 T|T 7 C|T 7 C|T 2 15882493 4 C|T 4 T|C 7 T|T 7 T|T 7 C|T 7 C|T 2 15882505 4 A|T 4 T|A 7 T|T 7 T|T 7 A|C 7 A|T Problem:
In the given data I want to solve the phase state of haplotype for the sample ms02g. The suffix PI represents the phased block (i.e all data within that block is phased).
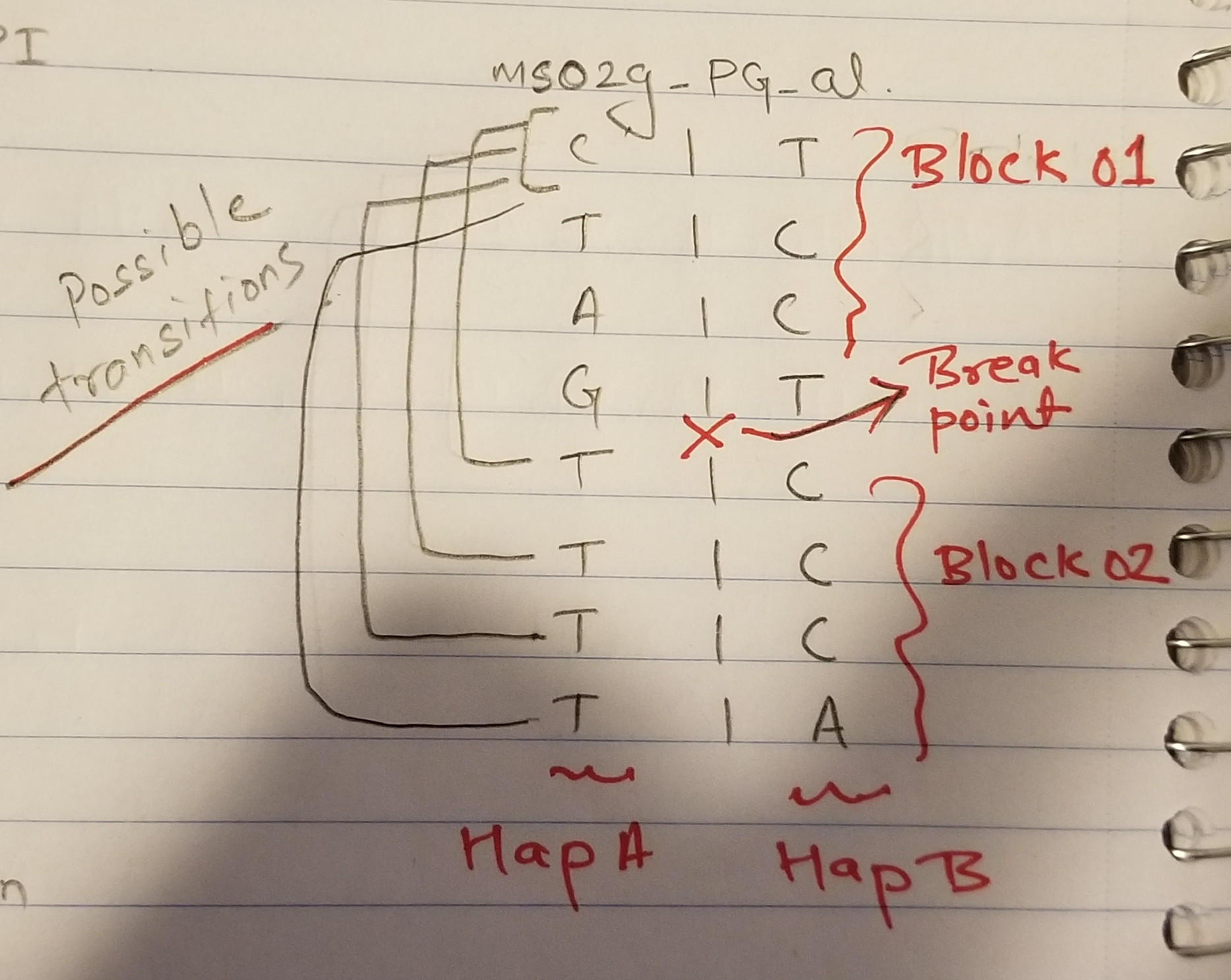
For sample ms02g C-T-A-G is phased (PI level 6), so is T-C-C-T. Similarly data within PI level 4 is also phased. But, since the haplotype is broken in two levels, we don't know which phase from level-6 goes with which phase of level-4. 
ms02g_PI ms02g_PG_al 6 C|T 6 T|C 6 A|C 6 G|T ×——————————×—————> Break Point 4 T|C 4 T|C 4 T|C 4 T|A Since, all other samples are completely phased I can run a markov-chain transition probabilities to solve the phase state. To the human eye/mind you can clearly see and say that left part of ms02g (level 6, i.e C-T-A-G is more likely to go with right block of level 4 C-C-C-A).
Calculation:
Step 01:
I prepare required haplotype configuration:
- The top haplotype-PI is
block01and bottom isblock-02. - The left phased haplotype within each block is
Hap-Aand the right isHap-B.
So, there are 2 haplotype configurations:
- Block01-HapA with Block02-HapA, so B01-HapB with B02-HapB
- Block01-HapA with Block02-HapB, so B01-HapB with B02-HapA
I count the number of transition for each nucleotide of PI-6 to each nucleotide of PI-4 for each haplotype configuration. 
Possible transitions ms02g_PG_al │ ┌┬┬┬ C|T │ ││││ T|C │ ││││ A|C │ ││││ G|T └─────> ││││ ×—————> Break Point │││└ T|C ││└─ T|C │└── T|C └─── T|A and multiply the transition probabilities for first nucleotide in PI-6 to all nucleotides of PI-4. Then similarly multiply the transition probability for 2nd nucleotide of PI-6 to all nucleotides in PI-4.
then I sum the transition probabilities from one level to another.
Possible transitions ms02g_PG_al │ ┌┬┬┬ C|T \ │ ││││ T|C | Block 1 │ ││││ A|C | │ ││││ G|T / └─────> ││││ ×—————> Break Point │││└ T|C \ ││└─ T|C | │└── T|C | Block 2 └─── T|A / ↓ ↓ Hap A Hap B Block-1-Hap-A with Block-2-Hap-B vs. Block-1-Hap-A with Block-2-Hap-A C|C × C|C × C|C × A|C = 0.58612 T|C × T|C × T|C × T|C = 0.000244 + C|T × C|T × C|T × A|T = 0.3164 + T|T × T|T × T|T × T|T = 0.00391 + C|A × C|A × C|A × A|A = 0.482 + T|A × T|A × T|A × T|A = 0.0007716 + C|G × C|G × C|G × A|G = 0.3164 + T|G × T|G × T|G × T|G = 0.00391 ——————— ————————— Avg = 0.42523 Avg = 0.002207 Likelyhood Ratio = 0.42523 / 0.002207 = 192.67 I have the following working code with python3: I think the transition probs can be mostly optimized using numpy, or using a markov-chain package. But, I was not able to work them out in the way I desired. Also, it took me sometime to get to what I wanted to do.
Any suggestions with explanation. Thanks.
#!/home/bin/python from __future__ import division import collections from itertools import product from itertools import islice import itertools import csv from pprint import pprint ''' function to count the number of transitions ''' def sum_Probs(pX_Y, pX): try: return float(pX_Y / pX) except ZeroDivisionError: return 0 with open("HaploBlock_Updated.txt", 'w') as f: ''' Write header (part 01): This is just a front part of the header. The rear part of the header is update dynamically depending upon the number of samples ''' f.write('\t'.join(['chr', 'pos', 'ms02g_PI', 'ms02g_PG_al', '\n'])) with open('HaploBlock_for_test-forHMMtoy02.txt') as Phased_Data: ''' Note: Create a dictionary to store required data. The Dict should contain information about two adjacent haplotype blocks that needs extending. In this example I want to extend the haplotypes for sample ms02g which has two blocks 6 and 4. So, I read the PI and PG value for this sample. Also, data should store with some unique keys. Some keys are: chr, pos, sample (PI, PG within sample), possible haplotypes ... etc .. ''' Phased_Dict = csv.DictReader(Phased_Data, delimiter='\t') grouped = itertools.groupby(Phased_Dict, key=lambda x: x['ms02g_PI']) ''' Function to read the data as blocks (based on PI values of ms02g) at a time''' def accumulate(data): acc = collections.OrderedDict() for d in data: for k, v in d.items(): acc.setdefault(k, []).append(v) return acc ''' Store data as keys,values ''' grouped_data = collections.OrderedDict() for k, g in grouped: grouped_data[k] = accumulate(g) ''' Clear memory ''' del Phased_Dict del grouped ''' Iterate over two Hap Blocks at once. This is done to obtain all possible Haplotype configurations between two blocks. The (keys,values) for first block is represented as k1,v2 and for the later block as k2,v2. ''' # Empty list for storing haplotypes from each block hap_Block1_A = []; hap_Block1_B = [] hap_Block2_A = []; hap_Block2_B = [] # Create empty list for possible haplotype configurations from above block hapB1A_hapB2A = [] hapB1B_hapB2B = [] ''' list of all available samples (index, value) ''' sample_list = [('ms01e_PI', 'ms01e_PG_al'), ('ms02g_PI', 'ms02g_PG_al'), ('ms03g_PI', 'ms03g_PG_al'), ('ms04h_PI', 'ms04h_PG_al'), ('ms05h_PI', 'ms05h_PG_al'), ('ms06h_PI', 'ms06h_PG_al')] ''' read data from two consecutive blocks at a time ''' for (k1, v1), (k2, v2) in zip(grouped_data.items(), islice(grouped_data.items(), 1, None)): ''' skip if one of the keys has no values''' if k1 == '.' or k2 == '.': continue ''' iterate over the first Haplotype Block, i.e the k1 block. The nucleotides in the left of the phased SNPs are called Block01-haplotype-A, and similarly on the right as Block01-haplotype-B. ''' hap_Block1_A = [x.split('|')[0] for x in v1['ms02g_PG_al']] # the left haplotype of Block01 hap_Block1_B = [x.split('|')[1] for x in v1['ms02g_PG_al']] ''' iterate over the second Haplotype Block, i.e the k2 block ''' hap_Block2_A = [x.split('|')[0] for x in v2['ms02g_PG_al']] hap_Block2_B = [x.split('|')[1] for x in v2['ms02g_PG_al']] ''' Now, we have to start to solve the possible haplotype configuration. Possible haplotype Configurations will be, Either : 1) Block01-haplotype-A phased with Block02-haplotype-A, creating -> hapB1A-hapB2A, hapB1B-hapB2B Or, 2) Block01-haplotype-A phased with Block02-haplotype-B creating -> hapB1A-hapB2B, hapB1B-hapB2A ''' ''' First possible configuration ''' hapB1A_hapB2A = [hap_Block1_A, hap_Block2_A] hapB1B_hapB2B = [hap_Block1_B, hap_Block2_B] ''' Second Possible Configuration ''' hapB1A_hapB2B = [hap_Block1_A, hap_Block2_B] hapB1B_hapB2A = [hap_Block1_B, hap_Block2_A] print('\nStarting MarkovChains') ''' Now, start preping the first order markov transition matrix for the observed haplotypes between two blocks.''' ''' To store the sum-values of the product of the transition probabilities. These sum are added as the product-of-transition is retured by nested for-loop; from "for m in range(....)" ''' Sum_Of_Product_of_Transition_probabilities_hapB1A_hapB2A = \ sumOf_PT_hapB1A_B2A = 0 Sum_Of_Product_of_Transition_probabilities_hapB1B_hapB2B = \ sumOf_PT_hapB1B_B2B = 0 Sum_Of_Product_of_Transition_probabilities_hapB1A_hapB2B = \ sumOf_PT_hapB1A_B2B = 0 Sum_Of_Product_of_Transition_probabilities_hapB1B_hapB2A = \ sumOf_PT_hapB1B_B2A = 0 for n in range(len(v1['ms02g_PI'])): # n-ranges from block01 ''' Set the probabilities of each nucleotides at Zero. They are updated for each level of "n" after reading the number of each nucleotides at that position. ''' pA = 0; pT = 0; pG = 0; pC = 0 # nucleotide_prob = [0., 0., 0., 0.] # or store as numpy matrix # Also storing these values as Dict # probably can be improved nucleotide_prob_dict = {'A': 0, 'T': 0, 'G': 0, 'C': 0} print('prob as Dict: ', nucleotide_prob_dict) ''' for storing the product-values of the transition probabilities. These are updated for each level of "n" paired with each level of "m". ''' product_of_transition_Probs_hapB1AB2A = POTP_hapB1AB2A = 1 product_of_transition_Probs_hapB1BB2B = POTP_hapB1BB2B = 1 product_of_transition_Probs_hapB1AB2B = POTP_hapB1AB2B = 1 product_of_transition_Probs_hapB1BB2A = POTP_hapB1BB2A = 1 ''' Now, we read each level of "m" to compute the transition from each level of "n" to each level of "m". ''' for m in range(len(v2['ms02g_PI'])): # m-ranges from block02 # transition for each level of 0-to-n level of V1 to 0-to-m level of V2 ''' set transition probabilities at Zero for each possible transition ''' pA_A = 0; pA_T = 0; pA_G = 0; pA_C = 0 pT_A = 0; pT_T = 0; pT_G = 0; pT_C = 0 pG_A = 0; pG_T = 0; pG_G = 0; pG_C = 0 pC_A = 0; pC_T = 0; pC_G = 0; pC_C = 0 ''' Also, creating an empty dictionary to store transition probabilities - probably upgrade using numpy ''' transition_prob_dict = {'A_A' : 0, 'A_T' : 0, 'A_G' : 0, 'A_C' : 0, 'T_A' : 0, 'T_T' : 0, 'T_G' : 0, 'T_C' : 0, 'G_A' : 0, 'G_T' : 0, 'G_G' : 0, 'G_C' : 0, 'C_A' : 0, 'C_T' : 0, 'C_G' : 0, 'C_C' : 0} ''' Now, loop through each sample to compute initial probs and transition probs ''' for x, y in sample_list: print('sample x and y:', x,y) ''' Update nucleotide probability for this site - only calculated from v1 and only once for each parse/iteration ''' if m == 0: pA += (v1[y][n].count('A')) pT += (v1[y][n].count('T')) pG += (v1[y][n].count('G')) pC += (v1[y][n].count('C')) nucleotide_prob_dict['A'] = pA nucleotide_prob_dict['T'] = pT nucleotide_prob_dict['G'] = pG nucleotide_prob_dict['C'] = pC nucleotide_prob = [pA, pT, pG, pC] ''' Now, update transition matrix ''' nucl_B1 = (v1[y][n]).split('|') # nucleotides at Block01 nucl_B2 = (v2[y][m]).split('|') # nucleotides at Block02 ''' create possible haplotype configurations between "n" and "m". If the index (PI value) are same we create zip, if index (PI value) are different we create product. ''' HapConfig = [] # create empty list if v1[x][n] == v2[x][m]: ziped_nuclB1B2 = [(x + '_' + y) for (x,y) in zip(nucl_B1, nucl_B2)] HapConfig = ziped_nuclB1B2 ''' Move this counting function else where ''' pA_A += (HapConfig.count('A_A')) # (v1[y][0].count('A'))/8 pA_T += (HapConfig.count('A_T')) pA_G += (HapConfig.count('A_G')) pA_C += (HapConfig.count('A_C')) pT_A += (HapConfig.count('T_A')) # (v1[y][0].count('A'))/8 pT_T += (HapConfig.count('T_T')) pT_G += (HapConfig.count('T_G')) pT_C += (HapConfig.count('T_C')) pG_A += (HapConfig.count('G_A')) # (v1[y][0].count('A'))/8 pG_T += (HapConfig.count('G_T')) pG_G += (HapConfig.count('G_G')) pG_C += (HapConfig.count('G_C')) pC_A += (HapConfig.count('C_A')) pC_T += (HapConfig.count('C_T')) pC_G += (HapConfig.count('C_G')) pC_C += (HapConfig.count('C_C')) if v1[x][n] != v2[x][m]: prod_nuclB1B2 = [(x + '_' + y) for (x,y) in product(nucl_B1, nucl_B2)] HapConfig = prod_nuclB1B2 print('prod NuclB1B2: ', prod_nuclB1B2) pA_A += (HapConfig.count('A_A'))/2 pA_T += (HapConfig.count('A_T'))/2 pA_G += (HapConfig.count('A_G'))/2 pA_C += (HapConfig.count('A_C'))/2 pT_A += (HapConfig.count('T_A'))/2 pT_T += (HapConfig.count('T_T'))/2 pT_G += (HapConfig.count('T_G'))/2 pT_C += (HapConfig.count('T_C'))/2 pG_A += (HapConfig.count('G_A'))/2 pG_T += (HapConfig.count('G_T'))/2 pG_G += (HapConfig.count('G_G'))/2 pG_C += (HapConfig.count('G_C'))/2 pC_A += (HapConfig.count('C_A'))/2 pC_T += (HapConfig.count('C_T'))/2 pC_G += (HapConfig.count('C_G'))/2 pC_C += (HapConfig.count('C_C'))/2 ''' Now, compute nucleotide and transition probabilities for each nucleotide from each 0-n to 0-m at each sample. This updates the transition matrix in each loop. **Note: At the end this transition probabilities should sum to 1 ''' ''' Storing nucleotide probabilities ''' nucleotide_prob = [pA, pT, pG, pC] ''' Storing transition probability as dict''' transition_prob_dict['A_A'] = sum_Probs(pA_A,pA) transition_prob_dict['A_T'] = sum_Probs(pA_T,pA) transition_prob_dict['A_G'] = sum_Probs(pA_G,pA) transition_prob_dict['A_C'] = sum_Probs(pA_C,pA) transition_prob_dict['T_A'] = sum_Probs(pT_A,pT) transition_prob_dict['T_T'] = sum_Probs(pT_T,pT) transition_prob_dict['T_G'] = sum_Probs(pT_G,pT) transition_prob_dict['T_C'] = sum_Probs(pT_C,pT) transition_prob_dict['G_A'] = sum_Probs(pG_A,pG) transition_prob_dict['G_T'] = sum_Probs(pG_T,pG) transition_prob_dict['G_G'] = sum_Probs(pG_G,pG) transition_prob_dict['G_C'] = sum_Probs(pG_C,pG) transition_prob_dict['C_A'] = sum_Probs(pC_A,pC) transition_prob_dict['C_T'] = sum_Probs(pC_T,pC) transition_prob_dict['C_G'] = sum_Probs(pC_G,pC) transition_prob_dict['C_C'] = sum_Probs(pC_C,pC) '''Now, we start solving the haplotype configurations after we have the required data (nucleotide and transition probabilities). Calculate joint probability for each haplotype configuration. Step 01: We calculate the product of the transition from one level of "n" to several levels of "m". ''' ''' finding possible configuration between "n" and "m". ''' hapB1A_hapB2A_transition = hapB1A_hapB2A[0][n] + '_' + hapB1A_hapB2A[1][m] hapB1B_hapB2B_transition = hapB1B_hapB2B[0][n] + '_' + hapB1B_hapB2B[1][m] hapB1A_hapB2B_transition = hapB1A_hapB2B[0][n] + '_' + hapB1A_hapB2B[1][m] hapB1B_hapB2A_transition = hapB1B_hapB2A[0][n] + '_' + hapB1B_hapB2A[1][m] ''' computing the products of transition probabilities on the for loop ''' POTP_hapB1AB2A *= transition_prob_dict[hapB1A_hapB2A_transition] POTP_hapB1BB2B *= transition_prob_dict[hapB1B_hapB2B_transition] POTP_hapB1AB2B *= transition_prob_dict[hapB1A_hapB2B_transition] POTP_hapB1BB2A *= transition_prob_dict[hapB1B_hapB2A_transition] ''' Step 02: sum of the product of the transition probabilities ''' sumOf_PT_hapB1A_B2A += POTP_hapB1AB2A sumOf_PT_hapB1B_B2B += POTP_hapB1BB2B sumOf_PT_hapB1A_B2B += POTP_hapB1AB2B sumOf_PT_hapB1B_B2A += POTP_hapB1BB2A ''' Step 03: Now, computing the likely hood of each haplotype configuration ''' print('computing likelyhood:') likelyhood_hapB1A_with_B2A_Vs_B2B = LH_hapB1AwB2AvsB2B = \ sumOf_PT_hapB1A_B2A / sumOf_PT_hapB1A_B2B likelyhood_hapB1B_with_B2B_Vs_B2A = LH_hapB1BwB2BvsB2A = \ sumOf_PT_hapB1B_B2B / sumOf_PT_hapB1B_B2A likelyhood_hapB1A_with_B2B_Vs_B2A = LH_hapB1AwB2BvsB2A = \ sumOf_PT_hapB1A_B2B / sumOf_PT_hapB1A_B2A likelyhood_hapB1B_with_B2A_Vs_B2B = LH_hapB1BwB2AvsB2B = \ sumOf_PT_hapB1B_B2A / sumOf_PT_hapB1B_B2B print('\nlikely hood Values: B1A with B2A vs. B2B, B1B with B2B vs. B2A') print(LH_hapB1AwB2AvsB2B, LH_hapB1BwB2BvsB2A) print('\nlikely hood Values: B1A with B2B vs. B2A, B1B with B2A vs. B2B') print(LH_hapB1AwB2BvsB2A, LH_hapB1BwB2AvsB2B) ''' Update the phase state of the block based on evidence ''' if (LH_hapB1AwB2AvsB2B + LH_hapB1BwB2BvsB2A) > \ 4*(LH_hapB1AwB2BvsB2A + LH_hapB1BwB2AvsB2B): print('Block-1_A is phased with Block-2_A') for x in range(len(v1['ms02g_PI'])): PI_value = v1['ms02g_PI'][x] # Note: so, we trasfer the PI value from ealier block to next block f.write('\t'.join([v1['chr'][x], v1['pos'][x], v1['ms02g_PI'][x], hapB1A_hapB2A[0][x] + '|' + hapB1B_hapB2B[0][x], '\n'])) for x in range(len(v2['ms02g_PI'])): f.write('\t'.join([v2['chr'][x], v2['pos'][x], PI_value, hapB1A_hapB2A[1][x] + '|' + hapB1B_hapB2B[1][x], '\n'])) elif (LH_hapB1AwB2AvsB2B + LH_hapB1BwB2BvsB2A) < \ 4 * (LH_hapB1AwB2BvsB2A + LH_hapB1BwB2AvsB2B): print('Block-1_A is phased with Block-2_B') for x in range(len(v1['ms02g_PI'])): PI_value = v1['ms02g_PI'][x] # Note: so, we trasfer the PI value from ealier block to next block... # but, the phase position are reversed f.write('\t'.join([v1['chr'][x], v1['pos'][x], v1['ms02g_PI'][x], hapB1A_hapB2A[0][x] + '|' + hapB1B_hapB2B[0][x], '\n'])) for x in range(len(v2['ms02g_PI'])): f.write('\t'.join([v2['chr'][x], v2['pos'][x], PI_value, hapB1B_hapB2B[1][x] + '|' + hapB1A_hapB2A[1][x], '\n'])) else: print('cannot solve the phase state with confidence - sorry ') for x in range(len(v1['ms02g_PI'])): f.write('\t'.join([v1['chr'][x], v1['pos'][x], v1['ms02g_PI'][x], hapB1A_hapB2A[0][x] + '|' + hapB1B_hapB2B[0][x], '\n'])) for x in range(len(v2['ms02g_PI'])): f.write('\t'.join([v2['chr'][x], v2['pos'][x], v2['ms02g_PI'][x], hapB1A_hapB2A[1][x] + '|' + hapB1B_hapB2B[1][x], '\n'])) 

performancetag, which is generally very dependent on the actual data. \$\endgroup\$