1
\$\begingroup\$

Answers to this explain why I can't reliably get int type arrays. While there are some workarounds I have a hunch there's a better, cleaner or otherwise "less tricky" way to get these hexagonal arrays of dots arranged in this spiral pattern than the way I've done it by using several conditions.

Is my hunch correct?

Note: hexit_60() and get_points() are used in different ways in other places so I don't want to combine them.

Context: This is used in a simulation and plotting routine for points in reciprocal space of a hexagonal lattice as part of a diffraction calculator.

hexagonal array of dots

import numpy as np import matplotlib.pyplot as plt def hexit_60(n_max): pairs = [] if n_max >= 0: pairs.append(np.zeros(2, dtype=int)[:, None]) if n_max >= 1: # https://stackoverflow.com/q/61382568/3904031 trap 0*[n] because casts to float seq = [1, 0, -1] p0 = np.hstack((seq, seq[::-1])) N = len(p0) p1 = np.hstack((p0[N-2:], p0[:N-2])) pairs.append(np.stack((p0, p1), axis=0)) for n in range(2, n_max+1): seq = np.arange(n, -n-1, -1, dtype=int) p0 = np.hstack((seq, (n-1)*[-n], seq[::-1], (n-1)*[n])) N = len(p0) p1 = np.hstack((p0[N-2*n:], p0[:N-2*n])) pairs.append(np.stack((p0, p1), axis=0)) if len(pairs) > 0: pairs = np.hstack(pairs) else: pairs = None return pairs def get_points(a, n_max): vecs = a * np.array([[1.0, 0.0], [0.5, 0.5*np.sqrt(3)]]) pairs = hexit_60(n_max = n_max) if isinstance(pairs, np.ndarray): points = (pairs[:, None]*vecs[..., None]).sum(axis=0) else: points = None return points fig = plt.figure() for i, n_max in enumerate([-1, 0, 1, 2, 3, 4]): ax = fig.add_subplot(2, 3, i+1) # plt.subplot(2, 3, i+1) ax.set_title('n_max: ' + str(n_max)) points = get_points(a=1.0, n_max=n_max) if isinstance(points, np.ndarray): x, y = points ax.scatter(x, y) ax.plot(x, y, '-k', linewidth=0.5) ax.set_xlim(-4.2, 4.2) ax.set_ylim(-4.2, 4.2) ax.set_aspect('equal') plt.show()
\$\endgroup\$

1 Answer 1

Reset to default
4
\$\begingroup\$

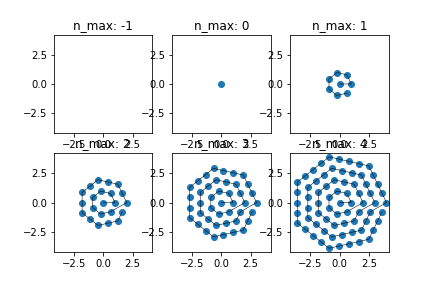
return early

For the special case, n_max == -1, you can return early

def hexit_60(n_max): if n_max == -1: return None

This allows you to simplify the loop a lot

special case

the part before the for-loop can be included in the main loop by taking one of the other answers to your int question, and use casting.

reverse

The reverse of seq is also the negative. If you extract the (n-1)*[-n] to another variable, you can make this a lot clearer.

np.roll

np.hstack((p0[N-2*n:], p0[:N-2*n])) is equivalent to np.roll(p0, 2 * n)

generator

You can make the hexit_60 into a generator, even further simplifying it

def hexit_60_gen(n_max): if n_max == -1: return yield np.zeros(2, dtype=int)[:, None] for n in range(1, n_max + 1): seq = np.arange(-n, n + 1, dtype=int) middle = np.array((n - 1) * [-n], dtype=int) p0 = np.hstack((-seq, middle, seq, -middle,)) p1 = np.roll(p0, 2 * n) yield np.vstack((p0, p1))

This code is a lot clearer to read to me.

It generates the same points:

all( np.array_equal( hexit_60(n_max), np.hstack(list(hexit_60_gen(n_max))) ) for n_max in range(10) )

get_points

You need to adapt this slightly:

def get_points_gen(a, n_max): vecs = a * np.array([[1.0, 0.0], [0.5, 0.5 * np.sqrt(3)]]) pairs = list(hexit_60_gen(n_max=n_max)) if pairs: return (np.hstack(pairs)[:, None] * vecs[..., None]).sum(axis=0)

if pairs is empty, this returns None implicitly.

The one thing I would is replace [0.5, 0.5 * np.sqrt(3)] by

angle = np.pi / 3 # diagonal [np.cos(angle), np.sin(angle)]

So you don't have as many magic numbers in the code

draw_hexagon

can be simplified with a slight reordering and a continue

def draw_hexagon(): fig = plt.figure() for i, n_max in enumerate([-1, 0, 1, 2, 3, 4]): ax = fig.add_subplot(2, 3, i+1) # plt.subplot(2, 3, i+1) ax.set_title('n_max: ' + str(n_max)) points = get_points_gen(a=1.0, n_max=n_max) ax.set_xlim(-4.2, 4.2) ax.set_ylim(-4.2, 4.2) if points is None: continue x, y = points ax.scatter(x, y) ax.plot(x, y, '-k', linewidth=0.5) ax.set_aspect('equal') plt.show()

This latest part can be made a bit cleaner, using the principles of clean architecture, but this is good enough, or a bit more parametrized, but this is good enough.

--

alternative approach

Instead of the approach of the hexit_60, you can have a function to assemble the first side of the hexagon, and then apply rotations to this:

ANGLE = np.pi / 3 COS_ANGLE = np.cos(ANGLE) SIN_ANGLE = np.sin(ANGLE) ROTATION_MATRIX = [[COS_ANGLE, -SIN_ANGLE], [SIN_ANGLE, COS_ANGLE]]

Then to get one side, using np.linspace to do the interpolation:

def side_points(n): if n == 0: return np.array([[0], [0]]) p0 = np.array([n, 0]) p1 = n * np.array([COS_ANGLE, SIN_ANGLE]) return np.linspace(p0, p1, n, endpoint=False).T

And then the rotations is a simple generator

def rotations(side): yield side if np.array_equal(side, np.array([[0], [0]])): return for _ in range(5): side = np.dot(ROTATION_MATRIX, side) yield side

Note that this can be easily adjusted to any regular polygon, by adjusting the angle, and passing in the appropriate cosinus, sinus and or rotation_matrix as function parameter instead of using the global

from functools import lru_cache @lru_cache(None) def cos_angle(sides): return np.cos(2 * np.pi / sides) @lru_cache(None) def sin_angle(sides): return np.sin(2 * np.pi / sides) @lru_cache(None) def rotation_matrix(sides): return np.array( [ [cos_angle(sides), -sin_angle(sides)], [sin_angle(sides), cos_angle(sides)], ] ) def side_points(n, sides=6): if n == 0: return np.array([[0], [0]]) p0 = np.array([n, 0]) p1 = n * np.array([cos_angle(sides), sin_angle(sides)]) return np.linspace(p0, p1, n, endpoint=False).T def rotations(side, sides=6): yield side if np.array_equal(side, np.array([[0], [0]])): return rot = rotation_matrix(sides) for _ in range(sides - 1): side = np.dot(rot, side) yield side def points(n_max, sides=6): return np.hstack( list( itertools.chain.from_iterable( rotations(side_points(n, sides), sides) for n in range(n_max + 1) ) ) )

Then drawing the polygon is simply:

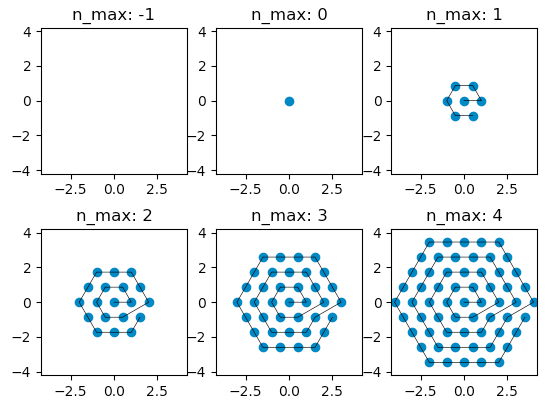
def draw_polygon(sides=6): fig = plt.figure() for i, n_max in enumerate([-1, 0, 1, 2, 3, 4]): ax = fig.add_subplot(2, 3, i + 1) # plt.subplot(2, 3, i+1) ax.set_title("n_max: " + str(n_max)) ax.set_xlim(-4.2, 4.2) ax.set_ylim(-4.2, 4.2) if n_max < 0: continue all_points = points(n_max, sides=sides) ax.scatter(*all_points) ax.plot(*all_points, "-k", linewidth=0.5) ax.set_aspect("equal") return fig 
draw_polygon(7)

enter image description here

\$\endgroup\$
4
  • 1
    \$\begingroup\$ Wow! This will take me a bit of time to review but I can tell already it's very helpful, thanks! \$\endgroup\$ Commented May 4, 2020 at 8:03
  • 1
    \$\begingroup\$ Nice answer. You don't show the actual call to draw_polygon that was used to make the plots. Are they supposed to be seven (7) sided polygons? \$\endgroup\$ Commented May 4, 2020 at 18:47
  • \$\begingroup\$ that is a 7-sided polygon indeed. I added the call in the code \$\endgroup\$ Commented May 4, 2020 at 19:43
  • \$\begingroup\$ Gee I can't keep up with the progress in your answer. :-) But the original post already solved my problem soI think in this case no need to hold out for further answers, this one's super, above, beyond etc.! \$\endgroup\$ Commented May 5, 2020 at 3:09

You must log in to answer this question.

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.