1
$\begingroup$

I just came across an exercise which is to find a regular expression for the following automaton, such that the regular expression and the automaton generate the same language.

NFA

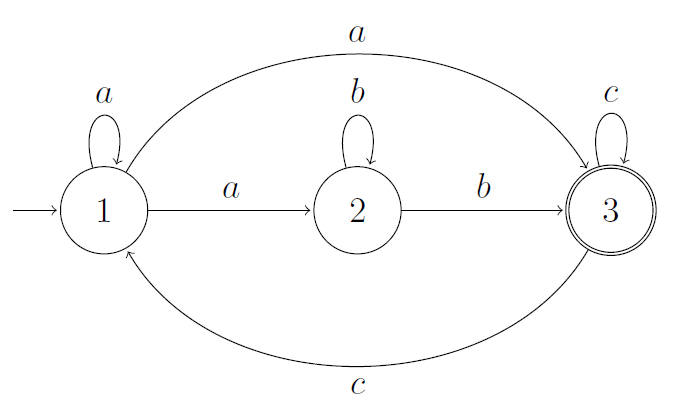
One solution presents the following expression:

$\qquad \displaystyle r_A = a^+b^+(c\mid ca^*b^+)^*$

However, can this be true? I think not, because the all words created from the regular expression will have at least one $b$ in it, whereas the automaton accepts words without $b$, such as $aaa$.

What is your opinion?

Improve this question
$\endgroup$
7
  • $\begingroup$ You already gave the answer, the DFA accepts a, but a is not contained in the language described by the RE. $\endgroup$ Commented Jul 21, 2012 at 13:56
  • $\begingroup$ It's pretty clear that the two are a mismatch, for the reason you give. Is there a reason why you doubt yourself? $\endgroup$ Commented Jul 21, 2012 at 14:10
  • $\begingroup$ It's pretty simple indeed. I doubted because it was the officially provided solution in a teaching book. I am going to send the author an e-mail or check the errata if I find them. Thanks! $\endgroup$ Commented Jul 21, 2012 at 14:26
  • 1
    $\begingroup$ I think it should be a+b*(c|ca+b*)* $\endgroup$ Commented Jul 21, 2012 at 17:56
  • 1
    $\begingroup$ Note that this question can be seen as too localized; you should try to formulate a more general question in most cases. Also note that we can use LaTeX here for typesetting maths. $\endgroup$ Commented Jul 23, 2012 at 7:41

2 Answers 2

Reset to default
2
$\begingroup$

In general, you can decide equivalence of regular expression and finite automaton using standard algorithms:

  • Construct an NFA from the regular expression,
  • Determinise and minimise both automata,
  • Check for equality (up to isomorphism).

These algorithms and proof that the minimal DFA of any regular language is unique (up to isomorphism) can be found in introductory textbooks.

If the underlying task is to "read off" a regular expression from an automaton, don't guess & proof but rather build the expression algorithmically to save time.

Improve this answer
$\endgroup$
2
  • $\begingroup$ You are absolutely right. But sometimes thinking saves time and improves your understanding before doing it the mechanical way ;) $\endgroup$ Commented Jul 23, 2012 at 14:19
  • 1
    $\begingroup$ @Erik Maybe I am no longer creative enough for such exercises, but what kind of thinking do you do? Trying inputs at random, hoping to refute correctness? Not very educational. Trying to find an intuitively correct mapping between expression and automaton? If that even exists for moderately complex cases, I doubt it will be worth the time. YMMV. $\endgroup$ Commented Jul 23, 2012 at 15:32
0
$\begingroup$

You can use formal methods like the elimination method.

However, in this specific case, since there is only one accepting state, and all the paths are directed to it - We can look at each path from the initial state to the accepting state and characterize it using regular expression. Then, we can perform union over the expressions we got, and maybe more manipulations.

  • Path 1 - upper - $a^*ac^*$
  • Path 2 - middle - $a^*ab^*bc^*$
  • Path 3 - lower - $a^*cc^*$

We can unify the shared parts and get:

$a^*(a + ab^*b + c)c^*$

(Btw - It's not necessarily a minimal regular expression for the language).

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.