I assume this is more reasonable to talk about error vectors not matrices in most cases. You have a vector is errors, only one column.
The parameters "m" and "c" in iyour example depends on the errors. Eventually they'll be picked in a way minimizing your cost function. They'll be different for MSE and MAE. The first one will try to make a mistake on outliers better.
Here I'm talking mostly about cost function but expect something similar for them in role of metrics as well.
Example:
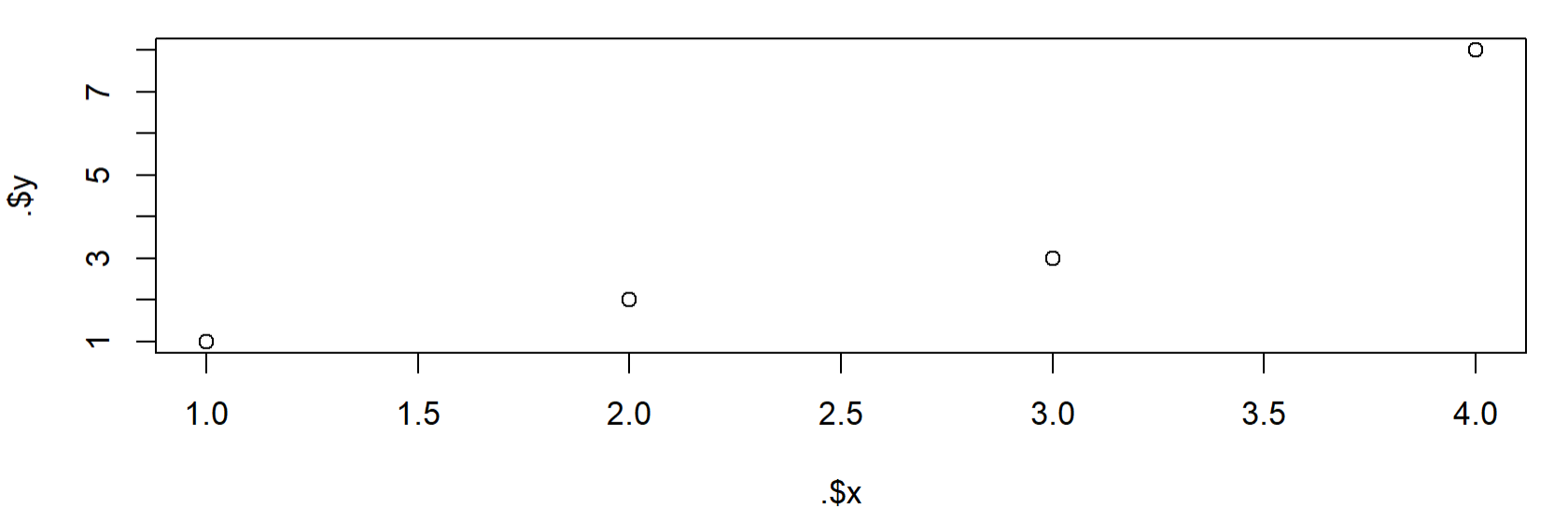
Here I create a 4 observations example. I use RMSE for comparision because MSE gives squared residuals, we want to get them back to the original non-squared scale at first. The first 3 observations imply a very plain model y = 1 * x + 0. Then I compare it with the model y = 2*x using residuals
> tibble(x=1:4, y=c(1,2,3,8)) %>% + {plot(.$x, .$y); .} %>% + mutate(base_pred=x * 1) %>% + mutate(outl_pred=x * 2) %>% + mutate(across(ends_with('pred'), ~abs(. - y), .names='{str_remove(col, "_pred")}_resi')) %>% + print() %>% + rename_with(~str_remove(., '_resi')) %>% + summarise(across(c(base, outl), list( + mae=~mean(.), + rmse=~sqrt(mean(. ^ 2))))) %>% + select(ends_with('mae'), everything()) x y base_pred outl_pred base_resi outl_resi <int> <dbl> <dbl> <dbl> <dbl> <dbl> 1 1 1 1 2 0 1 2 2 2 2 4 0 2 3 3 3 3 6 0 3 4 4 8 4 8 4 0 base_mae outl_mae base_rmse outl_rmse <dbl> <dbl> <dbl> <dbl> 1 1 1.5 2 1.87
You may see that base_model is better if you use MAE. Otherwise y=x*2 gives you better metric with RMSE because it suffers more and is more focused on outliers.

