Fitting Rotated Curve

Question

I'm trying to fit a rotated parabola with curve_fit, but it doesn't fit well as shown below:

I'm already trying to fit the curve with respect to the cos(𝜃) and sin(𝜃) dependency as follows:

def rotated_parabola(x, a, b, c, theta): # Original parabola y = a * x**2 + b * x + c # Rotate the parabola x_trans = x * np.cos(theta) - y * np.sin(theta) y_trans = x * np.sin(theta) + y * np.cos(theta) return x_trans, y_trans

Any insights as to why this isn't fitting well would be much appreciated, alternatively if there are any existing libraries which can solve this would be great too!

Thanks in advanced.

Hard to say without seeing the rest of your code but from the looks of things, it might be attempting to model f(x)=y when the actual relationship of your transformed data is f(y)=x. — AffableAmbler
– AffableAmbler, Commented Nov 1, 2024 at 20:27

MuhammedYunus · Accepted Answer · 2024-11-01 19:56:43Z

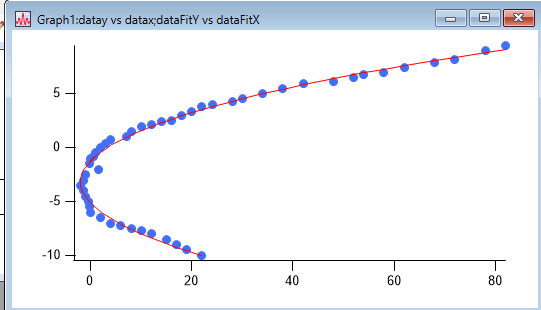
The approach below fits to a rotated parabola.

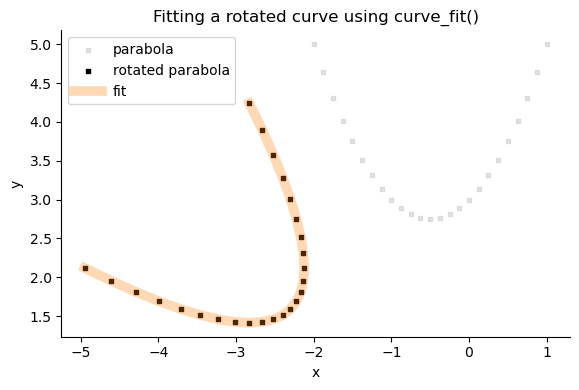
I estimate the coefficients $A, B, C$ by first removing the rotation (rotate $-\theta$). Then I plug in the coefficients of a regular parabola, and finally rotate the result back.

I give curve_fit() both the $x$ and $y$ coordinates (your code only supplies $x$ to the model).

The model function rotated_parabola() does the following:

Assume $x, y$ are in rotated space. Undo the rotation on $x$ by applying $-\theta$ to $x$.
Now it's a regular parabola, where we estimate $A, B, C$.
Rotate the estimated $y$ back to the original orientation by applying $\theta$.

Reproducible example

import numpy as np from scipy.optimize import curve_fit from matplotlib import pyplot as plt np.set_printoptions(suppress=True) # # Synthesise test data # It's a parabola defined by A, B, C, which is then rotated by THETA # THETA = 45 * np.pi/180 A, B, C = (1, 1, 3) #Generate the parabola defined by A, B, C data_x_parab = np.linspace(-2, 1, num=25) data_y_parab = A * data_x_parab**2 + B * data_x_parab + C #Rotate the parabola by THETA data_xy = (data_x, data_y) = ( np.row_stack([ (np.cos(THETA), -np.sin(THETA)), (np.sin(THETA), np.cos(THETA)) ]) @ np.row_stack([data_x_parab, data_y_parab]) ) def rotated_parabola(xy, theta, a, b, c): x, y = xy #First, apply -theta to reverse the rotation x_parabola = x * np.cos(-theta) - y * np.sin(-theta) # Parabola equation is now valid # Fit the parameters (a, b, c) of the parabola y_parabola = a * x_parabola**2 + b * x_parabola + c # Rotate the fitted point back into the original space y_fit = x_parabola * np.sin(theta) + y_parabola * np.cos(theta) return y_fit #Fit popt, pcov = curve_fit(rotated_parabola, data_xy, data_y) print( 'Data parameters:', THETA * 180/np.pi, A, B, C, '\n' 'Fitted parameters:', round(popt[0] * 180/np.pi), *popt[1:].round(1) ) # # Plot data # f, ax = plt.subplots(figsize=(8, 4), layout='tight') #Data ax.scatter(data_x_parab, data_y_parab, marker='s', s=12, alpha=0.1, color='black', label='parabola') ax.scatter(data_x, data_y, marker='s', s=12, color='black', label='rotated parabola') #Plot the fitted curve y_fitted = rotated_parabola(data_xy, *popt) ax.plot(data_x, y_fitted, color='tab:orange', linestyle='-', linewidth=7, alpha=0.3, label='fit') #Formatting ax.legend() ax.spines[['top', 'right']].set_visible(False) ax.set(xlabel='x', ylabel='y', title='Fitting a rotated curve using curve_fit()'); ax.set_aspect('equal')

kris_igor_pro · Accepted Answer · 2024-11-01 22:35:11Z

Here's how you do it in Igor Pro (https://www.wavemetrics.com/) assuming an x-wave named datax and a y-wave name datay:

Add the following function to your Procedures

Function fitRotatedParabola(Wave w, Variable x, Variable y) : FitFunc Variable a = w[0] Variable b = w[1] Variable c = w[2] Variable t = w[3] //CurveFitDialog/ //CurveFitDialog/ Coefficients 4 //CurveFitDialog/ w[0] = a //CurveFitDialog/ w[1] = b //CurveFitDialog/ w[2] = c //CurveFitDialog/ w[3] = t return a * (x * cos(t) - y * sin(t)) * (x * cos(t) - y * sin(t)) + b * (x * cos(t) - y * sin(t)) + c - x * sin(t) - y * cos(t) End

Create a coefficient wave as starting points for a, b, c, and theta:

Make /D /O rotatedParabolaCoefs = {2, 3, 3.5, 1.57079}

Duplicate the x and y waves to give the fit results somewhere to live:

Duplicate /O datax dataFitX Duplicate /O datay dataFitY

Run the fit:

FuncFit /ODR=3 fitRotatedParabola, rotatedParabolaCoefs /X={datax, datay} /XD={dataFitX, dataFitY}

Graph the results:

Display datay vs datax AppendToGraph dataFitY vs dataFitX ModifyGraph mode(datay)=3, marker(datay)=19, rgb(datay)=(1,16019,65535)

Stack Exchange Network

Fitting Rotated Curve

2 Answers 2

Reproducible example

Hot Network Questions

Fitting Rotated Curve

2 Answers 2

Reproducible example

Related

Hot Network Questions