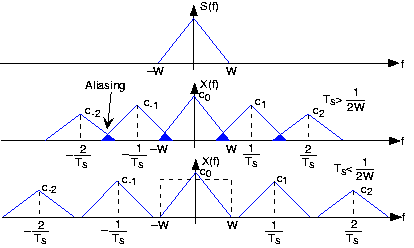
In this question, it has been proved that $x(t) = \sin(2\pi f_0 t)$ and $x_k(t) = \sin(2\pi (f_0 + k f_s) t)$ have the same sample points. So sinusoids with frequencies $f_0$ and $f_0 + kf_s$ will identify as the same signals. In other words, we keep sampling frequency constant and increase frequency by $kf_s$. Apparently, only frequencies $f_0 + kf_s$ lead to aliasing. Why this frequency is special? I tried to see this result in the frequency domain but it wasn't useful. I know by sampling in time domain we get shifted replicas of the original spectrum which is two delta functions at $f_0$ and $-f_0$ but how this corresponds to $f_s$ and aliasing at $f_0 + kf_s$? What I'm trying to get here is a visual explanation of mentioned result.

In this question, it has been proved that $x(t) = \sin(2\pi f_0 t)$ and $x_k(t) = \sin(2\pi (f_0 + k f_s) t)$ have the same sample points. So sinusoids with frequencies $f_0$ and $f_0 + kf_s$ will identify as the same signals. In other words, we keep sampling frequency constant and increase frequency by $kf_s$. Apparently, only frequencies $f_0 + kf_s$ lead to aliasing. Why this frequency is special? I tried to see this result in the frequency domain but it wasn't useful. I know by sampling in time domain we get shifted replicas of the original spectrum which is two delta functions at $f_0$ and $-f_0$ but how this corresponds to $f_s$ and aliasing at $f_0 + kf_s$? What I'm trying to get here is a visual explanation of mentioned result. In the case of the sampling theorem it's really easy to see aliasing occurs when there is an overlap.

In this question, it has been proved that $x(t) = \sin(2\pi f_0 t)$ and $x_k(t) = \sin(2\pi (f_0 + k f_s) t)$ have the same sample points. So sinusoids with frequencies $f_0$ and $f_0 + kf_s$ will identify as the same signals. In other words, we keep sampling frequency constant and increase frequency by $kf_s$. Apparently, only frequencies $f_0 + kf_s$ lead to aliasing. Why this frequency is special? I tried to see this result in the frequency domain but it wasn't useful. I know by sampling in time domain we get shifted replicas of the original spectrum which is two delta functions at $f_0$ and $-f_0$ but how this corresponds to $f_s$ and aliasing at $f_0 + kf_s$? What I'm trying to get here is the visual explanation of mentioned result.

In this question, it has been proved that $x(t) = \sin(2\pi f_0 t)$ and $x_k(t) = \sin(2\pi (f_0 + k f_s) t)$ have the same sample points. So sinusoids with frequencies $f_0$ and $f_0 + kf_s$ will identify as the same signals. In other words, we keep sampling frequency constant and increase frequency by $kf_s$. Apparently, only frequencies $f_0 + kf_s$ lead to aliasing. Why this frequency is special? I tried to see this result in the frequency domain but it wasn't useful. I know by sampling in time domain we get shifted replicas of the original spectrum which is two delta functions at $f_0$ and $-f_0$ but how this corresponds to $f_s$ and aliasing at $f_0 + kf_s$? What I'm trying to get here is a visual explanation of mentioned result.