0
$\begingroup$

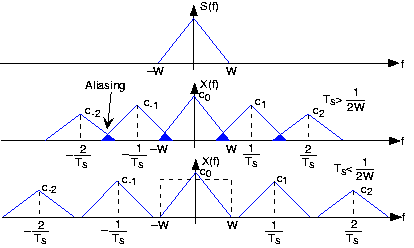
In this question, it has been proved that $x(t) = \sin(2\pi f_0 t)$ and $x_k(t) = \sin(2\pi (f_0 + k f_s) t)$ have the same sample points. So sinusoids with frequencies $f_0$ and $f_0 + kf_s$ will identify as the same signals. In other words, we keep sampling frequency constant and increase frequency by $kf_s$. Apparently, only frequencies $f_0 + kf_s$ lead to aliasing. Why this frequency is special? I tried to see this result in the frequency domain but it wasn't useful. I know by sampling in time domain we get shifted replicas of the original spectrum which is two delta functions at $f_0$ and $-f_0$ but how this corresponds to $f_s$ and aliasing at $f_0 + kf_s$? What I'm trying to get here is a visual explanation of mentioned result. In the case of the sampling theorem it's really easy to see aliasing occurs when there is an overlap.

enter image description here

Improve this question
$\endgroup$
5
  • $\begingroup$ there's nothing special here. You can pick any $f_0$! $\endgroup$ Commented Oct 12, 2020 at 21:54
  • $\begingroup$ @MarcusMüller My mean was aliasing occurs only at $f_0 + kf_s$. Obviously we can pick any $f_0$. $\endgroup$ Commented Oct 12, 2020 at 21:57
  • $\begingroup$ well, that's explained in the question you've linked to (and in hundreds of sources on aliasing) $\endgroup$ Commented Oct 12, 2020 at 21:58
  • $\begingroup$ @MarcusMüller I couldn't find a visual explanation for that special case of aliasing. Could you give me some references, please? $\endgroup$ Commented Oct 12, 2020 at 22:01
  • $\begingroup$ I don't understand – this is really not a special case. $\endgroup$ Commented Oct 13, 2020 at 21:16

1 Answer 1

Reset to default
2
$\begingroup$

You've made an error in this statement: "I know by sampling in time domain we get shifted replicas of the original spectrum which is two delta functions at $f_0$ and $−f_0$ but how this corresponds to $f_s$ and aliasing at $f_0+kf_s$?"

The two delta functions at $-f_0$ and $f_0$ are the result of taking the Fourier transform of a sinusoid $x(t)$:

$$ x(t) = \sin(2{\pi}f_0t)$$

$$\mathcal{F}(x(t)) = \frac{1}{2i} \big(\delta(f - f_0) + \delta(f + f_0) \big)$$

We haven't introduced sampling yet, this is simply the result of taking the Fourier transform. When we start sampling, then we introduce replicas of the signal's spectrum.

Let's assume we sample the $x(t)$ above at a frequency of $f_s$. We will have copies of that signal's spectrum at $f_0 + kf_s$ for all integer values of $k$. Assuming we met Nyquist, there's no problem here. The problem now comes when we have the sinusoid

$$ s(t) = \sin(2{\pi}(f_0 + f_s)t)$$

$$\mathcal{F}(s(t)) = \frac{1}{2i}\big( \delta(f - [f_0 + f_s]) + \delta(f + [f_0 + f_s]) \big)$$

When sampled, we have the spectrum copies centered at $(f_0 + f_s) + kf_s$ for all integer values of $k$. If we choose $k = -1$ then we have a copy at

$$ (f_0 + f_s) + kf_s|_{k = -1} = f_0$$

So if we had a combination of $x(t)$ and $s(t)$ and sampled it, a spectrum copy of $s(t)$ would step on $x(t)$'s copy at $f_0$. This is aliasing.

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.