Say I have a transfer function, for example:
$$H(z)=\frac{1}{1+0.1z^{-30}}$$
How can I compute the impulse response?
(This is just an example, the important thing is that it is in closed symbolic form!)
If I understand correctly, if I could just rewrite $H(z)$ as some polynomial in $z^-1$ (by using a Taylor expansion), I could just read off the coefficients.
But is there another way?
Your filter is the all-poles IIR, this simplifies things a bit. Normally you can write transfer function in following form:
$H(z)=\dfrac{\sum_{i=0}^{P}b_{i}z^{-i}}{\sum_{j=0}^{Q}a_{j}z^{-j}} $
Going back to the discrete time domain you will get:
$y[n] =\dfrac{1}{a_0}\left( \sum_{i=0}^{P}b_ix[n-i]-\sum_{j=1}^{Q}a_jy[n-j]\right)$
Therefore in your case it is:
$y[n]=x[n]-0.1y[n-30]$
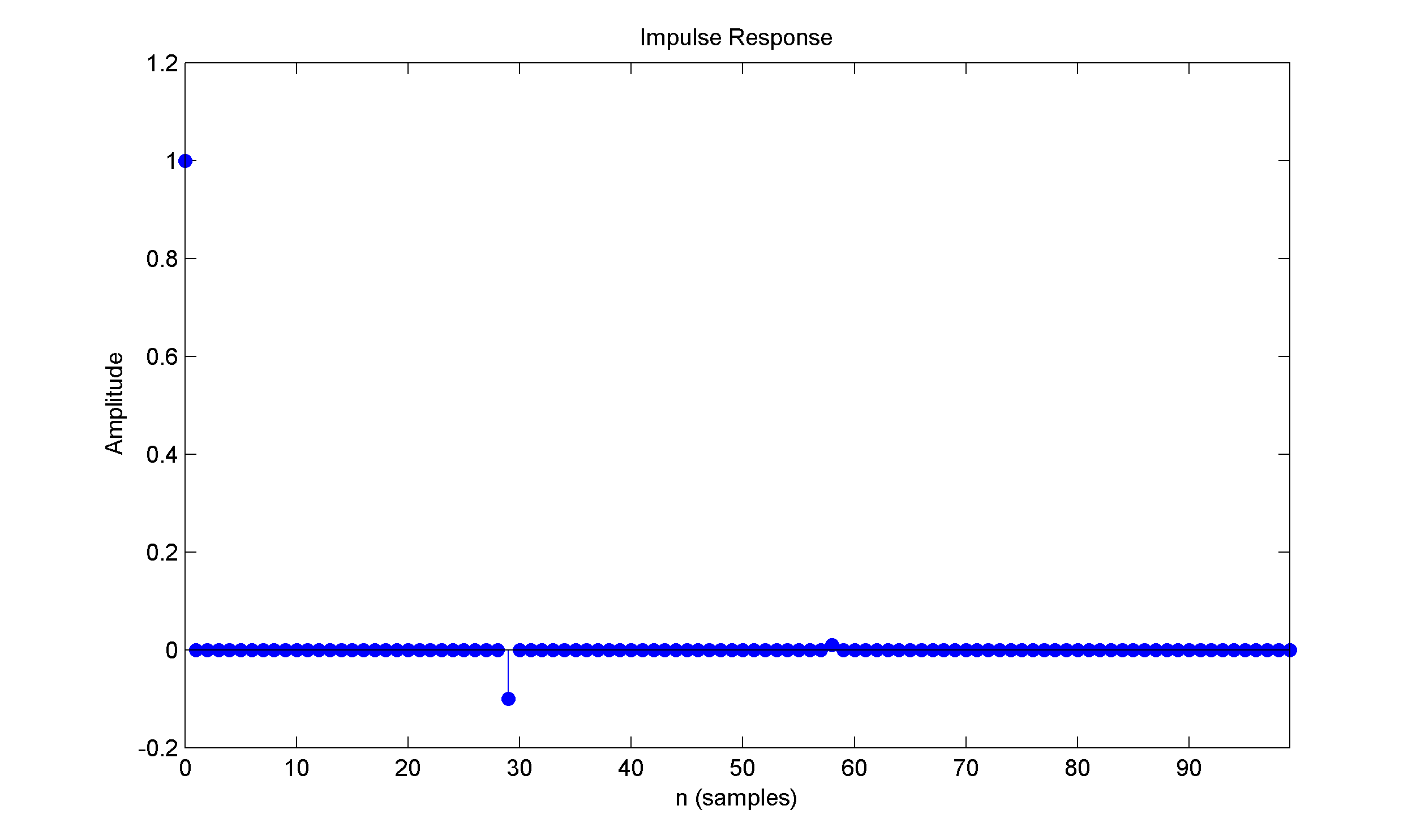
Calculation of particular values can be done by feeding Kronecker delta to your system ([1 0 0 0 0 0 0 ...] signal). Basically you will observe that something is happening every 30 samples ;) You can easily generate the plot in MATLAB/Octave, just remember that your filter has following coefficients:
b=[1] a=[1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.1] By calling impz(b,a) function you will get similar plot (first 100 samples): 
If your question is actually about implementing this transfer function, then you don't want to use its impulse response. Simply implement the difference equation correctly given in jolek's answer:
$$y[n]= x[n] - 0.1y[n-30],\quad y[-30]=y[-29]=\ldots=y[-1]=0\tag{1}$$
Only FIR filters are usually implemented directly using their (finite) impulse response. IIR filters are implemented by recursions, as given by (1).
