Let's follow option 1. I'm using Python but same is directly available in matlab. The partial fraction expansion can be found via residue function
>>> import scipy.signal as sig >>> b = [1, 1] >>> a = [1, 1, 0.5] >>> r, p, k = sig.residue(b,a) >>> r array([0.5-0.5j, 0.5+0.5j]) >>> p array([-0.5+0.5j, -0.5-0.5j]) >>> k array([0.])
This gives us $$ H(z) = \frac{0.5-0.5i}{z+0.5-0.5i} + \frac{0.5+0.5i}{z+0.5+0.5i} $$
Now either by computing manually, or using a Z-transform table, or using another computational tool you can show that these are two complex terms can be inversed transformed as
$$ \mathcal{Z}^{-1}\left[\frac{a}{z+a}\right] = \mathcal{Z}^{-1}\left[\frac{az^{-1}}{1+az^{-1}}\right] = -(-a)^k \mathbf{1}(k - 1) $$ Here $\mathbf{1}(k)$ is the discrete time step function. But since we have complex numbers this looks like our response should be a complex function. However this is not possible since our transfer function has real valued coefficients. Hence even before I compute anything, I know already that imaginary parts will cancel out.
And since $|a| < 1$ this is going to be a decaying sinusoidal. Indeed if we check this with say sampling period $T=1$,
>>> import harold as har >>> G = Transfer([1, 1], [1, 1, 0.5], dt=1) >>> impulse_response_plot(G);
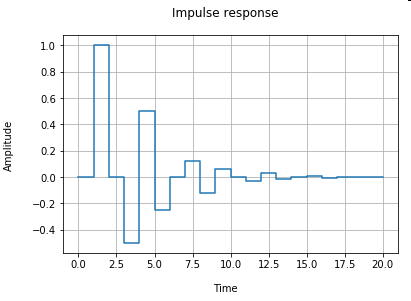
As expected, there is a one sample delay coming from $\mathbf{1}(k-1)$

