5
$\begingroup$

Could someone please help me with the following question?

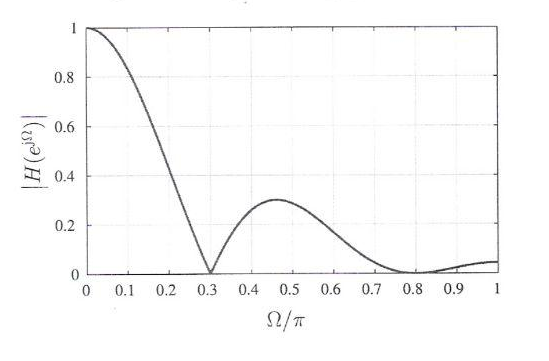
Below is the magnitude response of a real-valued causal linear phase FIR system of order N = 6. Determine the location of poles and zeros.

enter image description here

I know that for FIR systems all the poles are located at the origin, so we have a pole of order six at the origin. Also from the given diagram, I can say that we have a zero at 0.3pi and one at 0.8pi (both on the unit circle). Now since the system is real-valued, location of poles and zeros should be symmetric w.r.t. the real axis. But I don't know about the two other zeros?

Also, what about the pick in the diagram? Does it mean we have another pole?

Improve this question
$\endgroup$

2 Answers 2

Reset to default
11
$\begingroup$

Note the difference between the zeros at $0.3 \pi$ and at $0.8 \pi$.

The first one is clearly a zero crossing, much like $abs(x)$ at $x=0$.

At $\theta = 0.8 \pi$, however, the curve is tangent to the horizontal axis, much like $x^2$ at $x=0$. So you have a doulbe zero here.

So your zeros are:

  • 2 zeros at $z = e^{\pm j 0.3 \pi}$
  • 2 double zeros at $z = e^{\pm j 0.8 \pi}$
Improve this answer
$\endgroup$
1
$\begingroup$

Causality places the transfer-function poles at $z=0$, for a FIR filter.

A FIR filter need not necessarily be causal, in which case some or all of its poles reside at $z=\infty$ (if not at $z=0$). In any of these cases, the poles play no role in shaping frequency response, since they remain equidistant from the unit circle.

(A value of $k$ in the range of $[-1, 1]$ can place conjugate pole pairs anywhere on the unit circle, where they are most effectual in shaping frequency response.) $$\begin{aligned} \frac{z^2 +2kz + 1}{z^2} \ \ &\mbox{implies} \ \ y_n=x_n + 2kx_{n-1} + x_{n-2} \\ z^2 +2kz + 1 \ \ &\mbox{implies} \ \ y_n=x_{n+2} + 2kx_{n+1} + x_{n} \end{aligned}$$

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.