0
$\begingroup$

I'm new to the numerical processing of sampled measurements so my question is probably trivial. Let's suppose that I have the following sampled signal generated in MATLAB: 

>> fb = 3229; >> t = 0:(1 / (fb * 100)):150e-3; >> y = exp(1i * 2 * pi * fb * t);

(I know that the sampling frequency is much greater than the Nyquist one but it is only to get a finer representation of the function)
The Fourier Transform of my complex signal should be a single Dirac's Delta in fb = 3229 Hz. Now I get the DFT as follows: 

>> fy = fftshift(fft(y));

As expected, I get a single spectral line at approximately fb
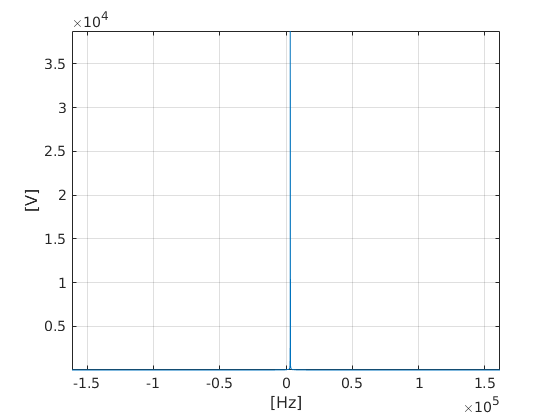
enter image description here

>> N = numel(fy); >> f_ax = (fb * 100) / N * ((- N / 2):(N / 2 - 1)); >> [~,idx] = max(abs(fy)) idx = 24703 >> f_ax(idx) ans = 3.2266e+03

However, the following returned phase is totally unexpected to me
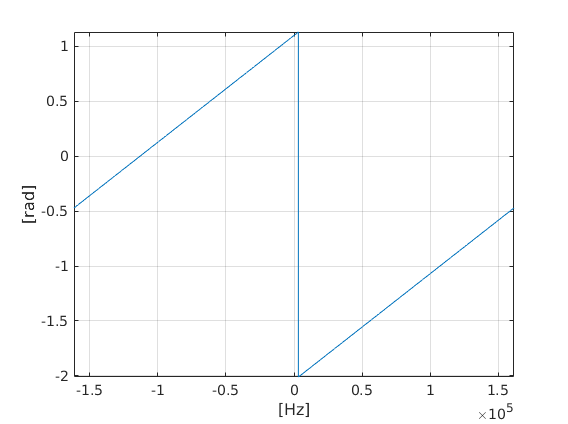
Phase of the DFT

I expected only a single spectral line in the modulus of the DFT and a phase equal to zero on the whole frequency axis. In particular, I get for the bin of fb the following phase

>> angle(fy(idx)) ans = 1.1310

Can someone explain me this behaviour? Thanks

Improve this question
$\endgroup$

3 Answers 3

Reset to default
2
$\begingroup$

You have to remember that the actual signal you have is not an ideal complex exponential extending infinitely in time, but a rectangularly windowed exponential. You can compute the DFT analytically:

$$X[k]=\sum_{n=0}^{N-1}e^{j2\pi f_0n}e^{j2\pi kn/N}\tag{1}$$

Using the formula for the geometric sum you'll end up with

$$X[k]=e^{j\pi(N-1)(f_0+k/N)}\frac{\sin\left[\pi N(f_o+k/N)\right]}{\sin\left[\pi (f_o+k/N)\right]}\tag{2}$$

From $(2)$ you see that the phase of the DFT is indeed linear:

$$\arg\{X[k]\}=\pi(N-1)(f_0+k/N)\tag{3}$$

Improve this answer
$\endgroup$
2
  • $\begingroup$ Thanks for your reply. I was missing the windowing. By using the geometric sum formula, I arrived to $(1 - e ^ {j 2 \pi N (f_0 + k / N)}) / (1 - e ^ {j 2 \pi (f_0 + k / N)})$. How did you get the expression in (2)? $\endgroup$ Commented Sep 9, 2019 at 14:57
  • $\begingroup$ @BullWebster: Just use $(1-e^{-j\phi})=e^{-j\phi /2}(e^{j\phi/2}-e^{-j\phi/2})=e^{-j\phi /2} 2j\sin(\phi/2)$. $\endgroup$ Commented Sep 9, 2019 at 16:25
0
$\begingroup$

I expected only a single spectral line in the modulus of the DFT

Your expectation is wrong. Your frequency sampling grid is your sample rate divided by the FFT length and your signal frequency is NOT an integer multiple of the sampling grid. Your sampling grid doesn't "hit" the exact location of the dirac, and so all the energy of the signal get's spread out over all frequency bins basically following a $sinc$ interpolation. The phase of this is well defined and that's exactly what you are seeing.

You don't see it in the amplitude because of poor scaling. Plot it in dB and you will easily see that the amplitudes are also non-zero at all frequencies.

Improve this answer
$\endgroup$
-1
$\begingroup$

The reason is that your phase is only defined at your dirac-delta impulse. The phase can be calculated as $\varphi = arcatan(\frac{Im(Z(f)}{Re(Z(f)})$ Whereby Z(f) is your DFT-Result.

Since Z(f) is zero besides at your frequency fb, the phase is something like $arcatan(\frac{"0"}{"0"})$

So the phase is only some numerical noise at frequencies not equal fb.

Improve this answer
$\endgroup$
3
  • $\begingroup$ What the OP sees is definitely no "numerical noise". $\endgroup$ Commented Aug 29, 2019 at 11:01
  • $\begingroup$ Sorry, that's wrong. You'd be correct only if the signal frequency would be an integer multiple of the FFT resolution $\endgroup$ Commented Aug 29, 2019 at 11:03
  • 2
    $\begingroup$ Oh I see. Was thinking about normal Fourier transform and did not think about seeing the leakage effect in the pase. Sorry for this wrong answer... at least I learned something $\endgroup$ Commented Aug 29, 2019 at 14:13

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.