2
$\begingroup$

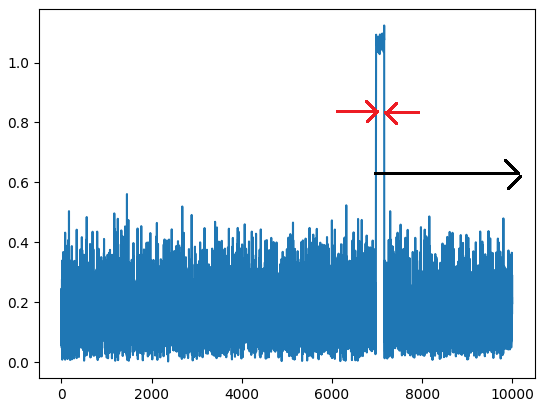
With python scipy I am processing (in real time) chunks of 250,000 each a CW pulsed beep radio signal in python from a RTLSDR. The signal after some basic processing and decimation is 9995 samples long and looks like:

A single chunk with a beep

A "beep" or high state as shown in the image above happens about once every 1,000,000 signals, and I process in chunks of 250,000 (before decimation). A high state has a duration of 189 samples (decimated).

The aim of the project is to:

 (a) Calculate time between beeps (black arrow); (b) Calculate beep length (red arrows)

I have tried a few techniques to smooth the signal in the picture (and improve SNR) but they are affecting the downstream calculations.

Moving Average Smoothing:

np.convolve(max_samples, [1]*189, 'valid')/189

Introduced artifacts on the padding edges, which caused downstream calculations particularly where a chunk edge slices the beginning of a rising edge because the "rising edge" largely disappears and is no longer detected.

padding issues

Savitzky-Golay

https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.savgol_filter.html#scipy.signal.savgol_filter

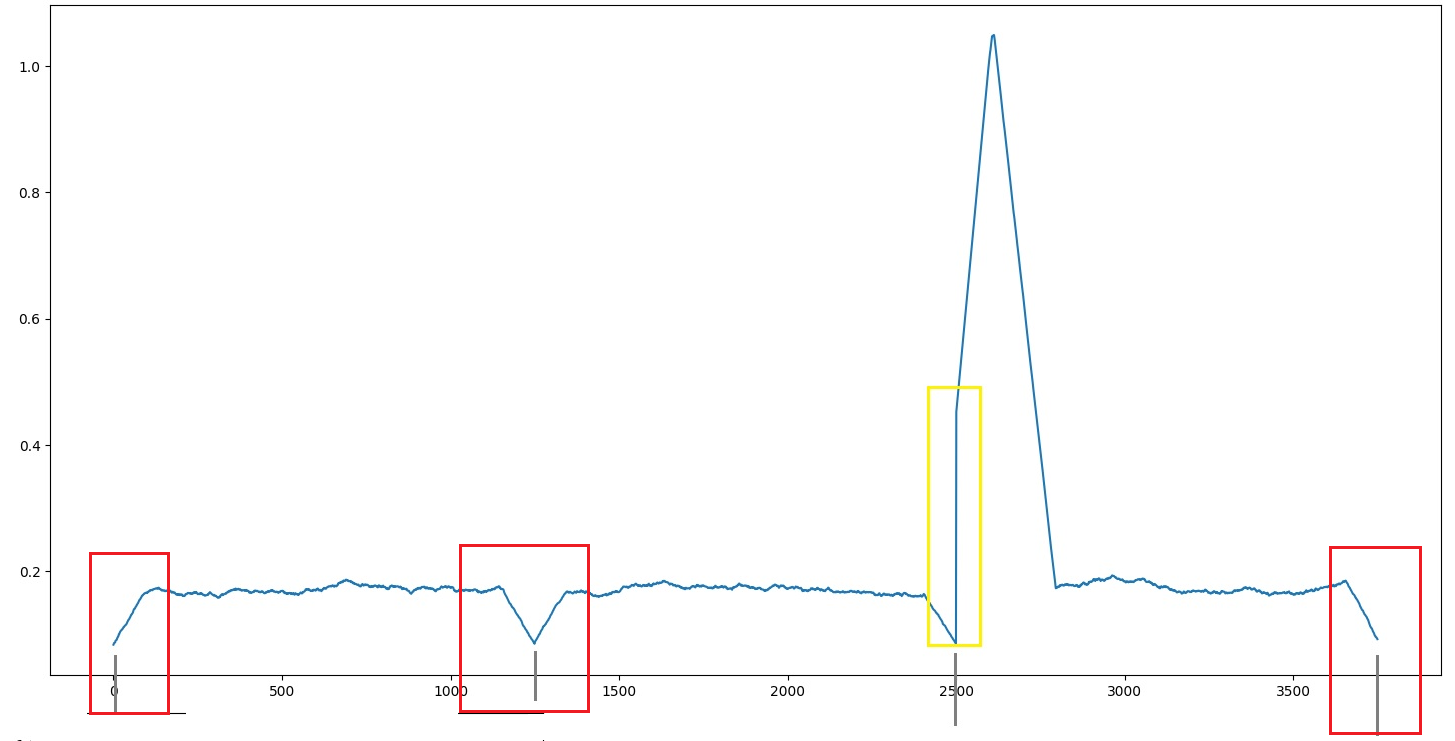
signal.savgol_filter(max_samples, 189, 50)

I could not get this filter to output any plot that made sense:

Savitzky Golay

Is there a better way to deal with the smoothing issue, especially as it relates to where a chunk has sliced a beeps rising edge, and still accurately calculating a beeps length?

If the answer is in the Savitzky Golay filter - what are sensible values? When I tried values like:

I get stack error:

-> 630 raise ValueError( 631 "array must not contain infs or NaNs") 632 return a
Improve this question
$\endgroup$
8
  • $\begingroup$ The error says you have nans or infs. Get rid of those (set them to the mean value for example). $\endgroup$ Commented Apr 8, 2024 at 11:29
  • 1
    $\begingroup$ Are the beeps consistent? I’m asking because in your example, there is a clear threshold over which the beep happens. For this particular example, you could set it at say $0.8$, and the crossings at that threshold define your beep in time… $\endgroup$ Commented Apr 8, 2024 at 11:31
  • $\begingroup$ Why don't you run this through a simple thresholder? Smoothing will always mess up the edges no matter how you do it. $\endgroup$ Commented Apr 8, 2024 at 14:50
  • $\begingroup$ Thats a perfect signal - add noise, and the smoothing is useful in getting the signal out of the noise. (So no the beeps are not always that clear. $\endgroup$ Commented Apr 9, 2024 at 1:52
  • $\begingroup$ @jdip I don't know how NaN or Inf get into the max_samples - there is valid numbers in the array. $\endgroup$ Commented Apr 9, 2024 at 2:11

2 Answers 2

Reset to default
3
$\begingroup$

This seems to boil down to an edge detection problem. Since we need to preserve edges, typically a smoothing filter won't produce great results. There are two other methods that would probably work very well (or perhaps even better in combination), especially if the example the OP showed is representative.

The first technique is Total Variation Denoising (TVD). It is an edge preserving smoothing algorithm, so the output should look more like a clean train of rectangular beeps. Once you have this, it might be as simple as taking the difference between adjacent samples to find edges (a large positive difference is a rising edge, and a large negative difference is a falling edge).

The second technique, which could be used independently or after TVD, is a 1D Canny edge detector. Developed by John Canny in 1986, it is considered a mathematically optimal edge detector in some sense.

Code Packages

For 1D TVD in Python, the TVDCondat2013 package looks good, though there are probably others if you search around.

There are many Python packages for 2D Canny edge detection (for images), but I haven't come across any for 1D. Perhaps some of the 2D ones adapt readily to 1D. On the other hand, the Canny concept is well known, to the point that chatGPT offered to quickly write me a 1D version which worked reasonably well on a one-off example. So you could probably write a basic one fairly easily.

Outside of Python, you can find a 1D Canny edge detector package in MATLAB here. It is old, so you have to use archive.org to download it. The download package includes excellent documentation. It is not a lot of code, so you could easily translate it to Python yourself, or even using an AI.

Improve this answer
$\endgroup$
1
  • $\begingroup$ I have marked this as answer, although in the end I just padded my samples so that I never had to deal with the edge detection problem. $\endgroup$ Commented Jun 8 at 11:36
0
$\begingroup$

As a suggestion, since you know the shape of the beep is a rectangular pulse, take inspiration from image edge detection by computing the unnormalised cross correlation between your signal and a pattern matching the ideal beep edge. This combines edge detection and filtering to increase the signal-to-noise ratio into a single operation to achieve your objectives.

The pattern should consist of -1 for one half and +1 for the other half. You stated that the beep high duration is nominally 189 samples long, but since your objective is to measure this, I presume it must have some variation. The overall pattern length should be no more than twice the shortest duration beep you can guarantee will occur. This pattern weights all points equally, which is ideal for attenuating random noise, with the increase in signal-to-noise ratio being equal to the square root of the pattern length. For example, the pattern might be -1 for 100 samples followed by +1 for 100 samples, which would increase your signal-to-noise ratio by over 14 times.

Rising beep edges will correspond to maxima in the cross-correlation, and the falling beep edges will correspond to minima. Only consider maxima and minima that have an absolute magnitude greater than a threshold you define to reject noise. Using my aforementioned pattern example, and noting that in your plot the beep height is approximately 1, an absolute threshold of 80 might be appropriate given the cross-correlation will result in a value of approximately 100, thus this gives some tolerance for lower height beeps.

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.