How to find Thevenin equivalent of this circuit? Dependent current source

First, I will present a method that uses Mathematica to solve this problem. When I was studying this stuff I used the method all the time (without using Mathematica of course).

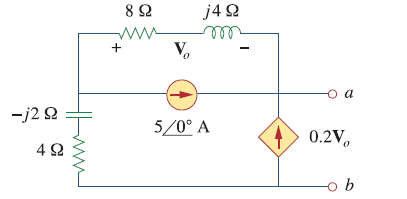
Well, we are trying to analyze the following circuit:

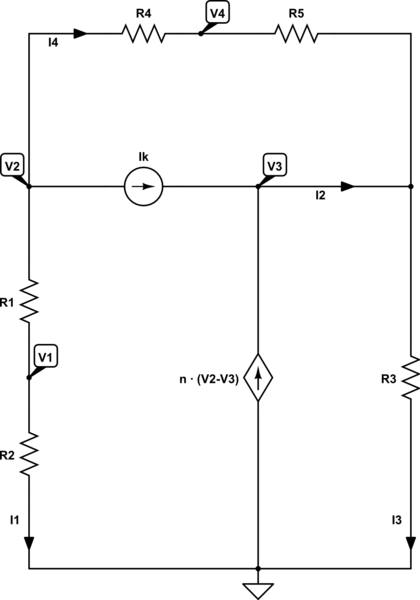
^{simulate this circuit – Schematic created using CircuitLab}

When we use and apply KCL, we can write the following set of equations:

$$ \begin{cases} 0=\text{I}_\text{k}+\text{I}_1+\text{I}_4\\ \\ \text{I}_2=\text{I}_\text{k}+\text{n}\cdot\left(\text{V}_2-\text{V}_3\right)\\ \\ \text{I}_3=\text{I}_2+\text{I}_4\\ \\ \text{n}\cdot\left(\text{V}_2-\text{V}_3\right)=\text{I}_1+\text{I}_3 \end{cases}\tag1 $$

When we use and apply Ohm's law, we can write the following set of equations:

$$ \begin{cases} \text{I}_1=\frac{\text{V}_2-\text{V}_1}{\text{R}_1}\\ \\ \text{I}_1=\frac{\text{V}_1}{\text{R}_2}\\ \\ \text{I}_3=\frac{\text{V}_3}{\text{R}_3}\\ \\ \text{I}_4=\frac{\text{V}_2-\text{V}_4}{\text{R}_4}\\ \\ \text{I}_4=\frac{\text{V}_4-\text{V}_3}{\text{R}_5} \end{cases}\tag2 $$

Now, we can set-up a Mathematica-code to solve for all the voltages and currents:

In[1]:=FullSimplify[ Solve[{0 == Ik + I1 + I4, I2 == Ik + n*(V2 - V3), I3 == I2 + I4, n*(V2 - V3) == I1 + I3, I1 == (V2 - V1)/R1, I1 == V1/R2, I3 == V3/R3, I4 == (V2 - V4)/R4, I4 == (V4 - V3)/R5}, {I1, I2, I3, I4, V1, V2, V3, V4}]] Out[1]={{I1 -> -((Ik (1 + n R3) (R4 + R5))/( R1 + R2 + R3 + R4 + R5 + n R3 (R4 + R5))), I2 -> (Ik (R1 + R2 + R3 + R4 + R5 - n R1 (R4 + R5) - n R2 (R4 + R5)))/(R1 + R2 + R3 + R4 + R5 + n R3 (R4 + R5)), I3 -> -((Ik (-1 + n (R1 + R2)) (R4 + R5))/( R1 + R2 + R3 + R4 + R5 + n R3 (R4 + R5))), I4 -> -((Ik (R1 + R2 + R3))/( R1 + R2 + R3 + R4 + R5 + n R3 (R4 + R5))), V1 -> -((Ik R2 (1 + n R3) (R4 + R5))/( R1 + R2 + R3 + R4 + R5 + n R3 (R4 + R5))), V2 -> -((Ik (R1 + R2) (1 + n R3) (R4 + R5))/( R1 + R2 + R3 + R4 + R5 + n R3 (R4 + R5))), V3 -> -((Ik (-1 + n (R1 + R2)) R3 (R4 + R5))/( R1 + R2 + R3 + R4 + R5 + n R3 (R4 + R5))), V4 -> Ik (R4 - ((1 + n R3) (R1 + R2 + R4) (R4 + R5))/( R1 + R2 + R3 + R4 + R5 + n R3 (R4 + R5)))}} 

Now, we can find:

• \$\text{V}_\text{th}\$ we get by finding \$\text{V}_3\$ and letting \$\text{R}_3\to\infty\$: $$\text{V}_\text{th}=\frac{\text{I}_\text{k}\left(\text{R}_4+\text{R}_5\right)\left(1-\text{n}\left(\text{R}_1+\text{R}_2\right)\right)}{\text{n}\left(\text{R}_4+\text{R}_5\right)+1}\tag3$$
• \$\text{I}_\text{th}\$ we get by finding \$\text{I}_3\$ and letting \$\text{R}_3\to0\$: $$\text{I}_\text{th}=\frac{\text{I}_\text{k}\left(\text{R}_4+\text{R}_5\right)\left(1-\text{n}\left(\text{R}_1+\text{R}_2\right)\right)}{\text{R}_1+\text{R}_2+\text{R}_4+\text{R}_5}\tag4$$
• \$\text{R}_\text{th}\$ we get by finding: $$\text{R}_\text{th}=\frac{\text{V}_\text{th}}{\text{I}_\text{th}}=\frac{\text{R}_1+\text{R}_2+\text{R}_4+\text{R}_5}{\text{n}\left(\text{R}_4+\text{R}_5\right)+1}\tag5$$

Where I used the following Mathematica-codes:

In[2]:=FullSimplify[ Limit[-((Ik (-1 + n (R1 + R2)) R3 (R4 + R5))/( R1 + R2 + R3 + R4 + R5 + n R3 (R4 + R5))), R3 -> Infinity]] Out[2]=-((Ik (-1 + n (R1 + R2)) (R4 + R5))/(1 + n (R4 + R5))) In[3]:=FullSimplify[ Limit[-((Ik (-1 + n (R1 + R2)) (R4 + R5))/( R1 + R2 + R3 + R4 + R5 + n R3 (R4 + R5))), R3 -> 0]] Out[3]=-((Ik (-1 + n (R1 + R2)) (R4 + R5))/(R1 + R2 + R4 + R5)) In[4]:=FullSimplify[%2/%3] Out[4]=(R1 + R2 + R4 + R5)/(1 + n (R4 + R5)) 

Now, using your values we get:

• $$\underline{\text{V}}_{\space\text{th}}=\frac{80}{37}+\frac{260}{37}\cdot\text{j}\tag6$$
• $$\underline{\text{I}}_{\space\text{th}}=\frac{10}{37}+\frac{60}{37}\cdot\text{j}\tag7$$
• $$\underline{\text{Z}}_{\space\text{th}}=\frac{164}{37}-\frac{22}{37}\cdot\text{j}\tag8$$

Where \$\underline{x}\$ implies that the value is a complex number, so \$\underline{x}\in\mathbb{C}\$.