How can I analyze the circuit shown in the diagram below using either nodal analysis or mesh analysis? I attempted solving the problem using mesh but ended up with the wrong answer.
To obtain the correct answer, I must obtain the differential equation: dv/dt + 0.25v = 0 and not dv/dt + 0.75v = 0 as shown in the working. Can anyone tell me what it is I am doing wrong?
Well, we have the following circuit:
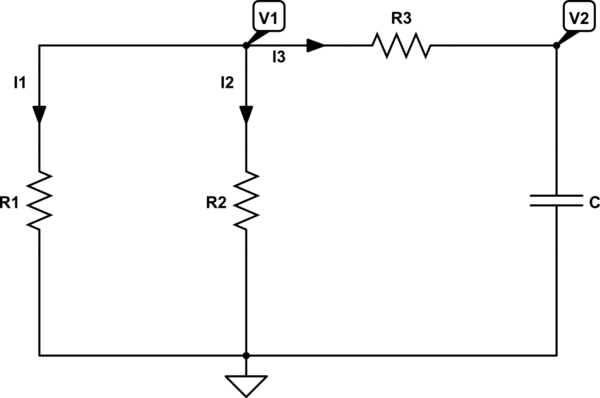
simulate this circuit – Schematic created using CircuitLab
Using KCL, we can see that:
$$0=\text{I}_1\left(t\right)+\text{I}_2\left(t\right)+\text{I}_3\left(t\right)\tag1$$
And for the voltages we can see:
$$ \begin{cases} \begin{alignat*}{1} \text{I}_1\left(t\right)&=\frac{\displaystyle\text{V}_1\left(t\right)-0}{\displaystyle\text{R}_1}\\ \\ \text{I}_2\left(t\right)&=\frac{\displaystyle\text{V}_1\left(t\right)-0}{\displaystyle\text{R}_2}\\ \\ \text{I}_3\left(t\right)&=\frac{\displaystyle\text{V}_1\left(t\right)-\text{V}_2\left(t\right)}{\displaystyle\text{R}_3}\\ \\ \text{I}_3\left(t\right)&=\left(\text{V}_2'\left(t\right)-0\right)\text{C} \end{alignat*} \end{cases} \tag2 $$
Combinging, gives:
$$ \begin{cases} \begin{alignat*}{1} 0&=\frac{\displaystyle\text{V}_1\left(t\right)-0}{\displaystyle\text{R}_1}+\frac{\displaystyle\text{V}_1\left(t\right)-0}{\displaystyle\text{R}_2}+\frac{\displaystyle\text{V}_1\left(t\right)-\text{V}_2\left(t\right)}{\displaystyle\text{R}_3}\\ \\ 0&=\frac{\displaystyle\text{V}_1\left(t\right)-0}{\displaystyle\text{R}_1}+\frac{\displaystyle\text{V}_1\left(t\right)-0}{\displaystyle\text{R}_2}+\left(\text{V}_2'\left(t\right)-0\right)\text{C} \end{alignat*} \end{cases} \tag3 $$
Which is really easy to solve :).
