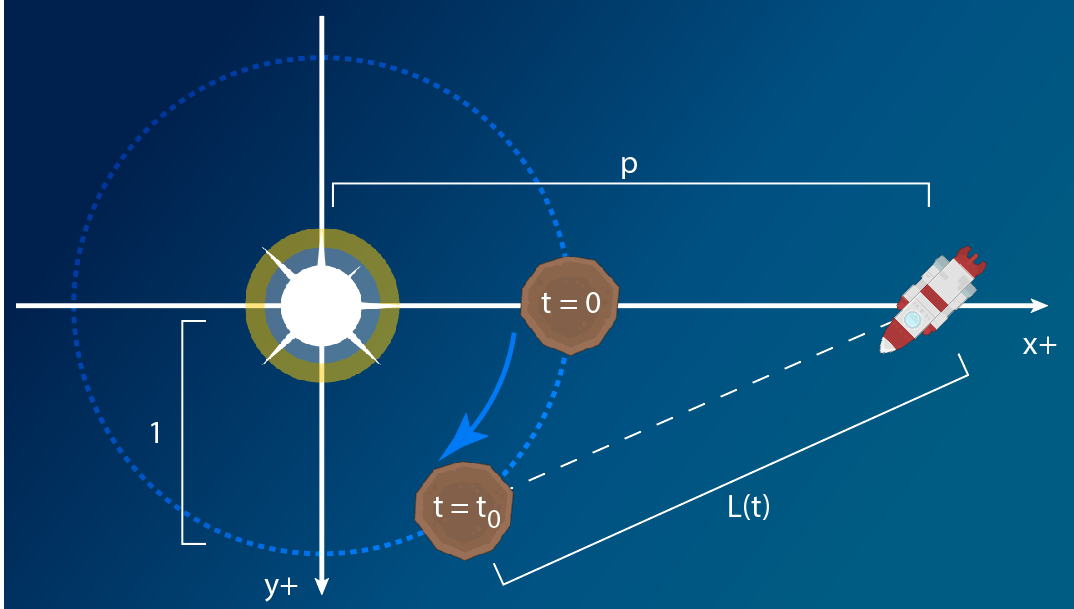
Define the center of the planet's orbit as the origin
Define the radius of the orbit as 1 (effectively our distances are now measured in AU)
Define our unit of time as the duration it takes the planet to travel 1 unit of space (so now 1 planetary year = 2 pi time units)
Define time 0
t=0as the most recent moment that the planet passed between the spaceship's start position and the center of the orbit, and time t_0 is the "start" time when our ship begins moving from that location
t_0, the time forward from which we want to find solutions:
t_0 = angleDifference(planetStartAngle, atan2(shipStartPosition - orbitCenter)) if(t_0 < 0) t_0 += 2 * piThis is just the clockwise (orbit-wise) angle in radians between the ship's start position and the planet's, as viewed from the center of the orbit. Starting from perfect alignment with the ship at t = 0, the planet needs to orbit through angle t_0 before it arrives at its start position relative to the ship.
p, the scalar distance of the ship's start position from the center of the orbit:
p = length(shipStartPosition - orbitCenter)/orbitRadiuss, the speed of the ship in our new spacetime coordinate system's scale:
s = shipSpeed * 2 * pi / (planetAngularSpeed * orbitRadius)
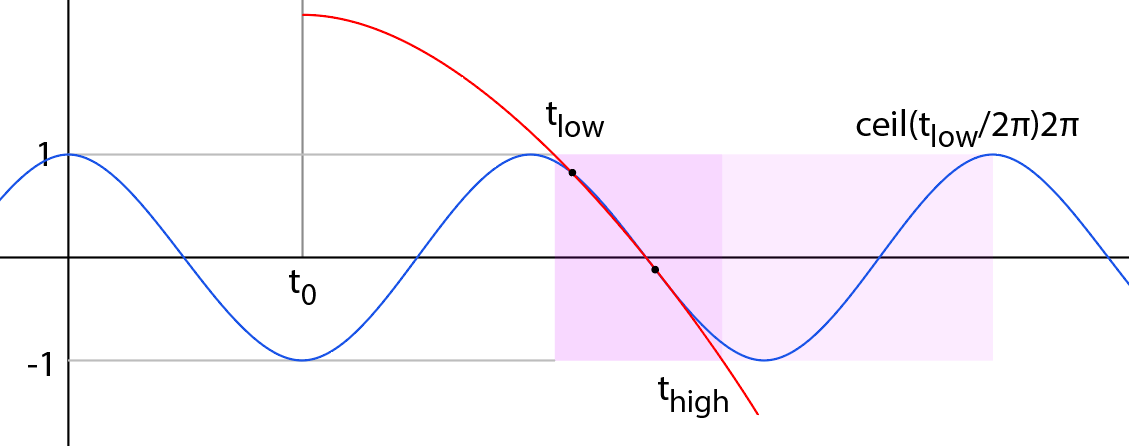
We know the cosine wave rises back up to 1 by t_high = t_low + 2pit_high = ceil(t_low/2pi)*2pi, but the parabola is strictly decreasing, so our earliest intersection must lie between t_lowt_low and t_hight_high, a singleat most one wavelength apart.
Unfortunately this seems to be about as far as a pure analytical approach can take us, and we're again forced to use some type of iterative root finding method in this span, but at least we've reduced it to about the simplest case we could hope for. There could still be multiple roots in this span, but our bounds are tight enough that this should be rare.
If your planet orbits much faster than your ship moves, the parabola will be nearly flat in this span and you can closely approximate it as a constant, using acos to find a very close first guess between t_low and t_high. Or if your ship travels much faster than your planet, the parabola will be nearly vertical the solution will be quite close to t_lowt_low. For intermediate cases like the example above, you might be able to approximate each curve as a straight line and iteratively refine from there.