Return to Revisions

I don't think a purely analytical solution to this is possible.

Any way we slice it, we have part of the problem in polar coordinates and another part in cartesian coordinates. So we end up trying to find an intersection between a line or curve and a sinusoid/periodic trig function. If the line were a constant we could use the arcsine/arccosine/arctangent functions. But unfortunately we're dealing with curves or lines with slope so no standard function gets us what we need.

In a previous answer I showed how we can solve this to within the needed accuracy by binary search. But since you've specified you don't want to solve it that way, let's see if we can reframe our problem differently.

First, to simplify our math, let's apply some (reversible) changes of coordinate system and units.

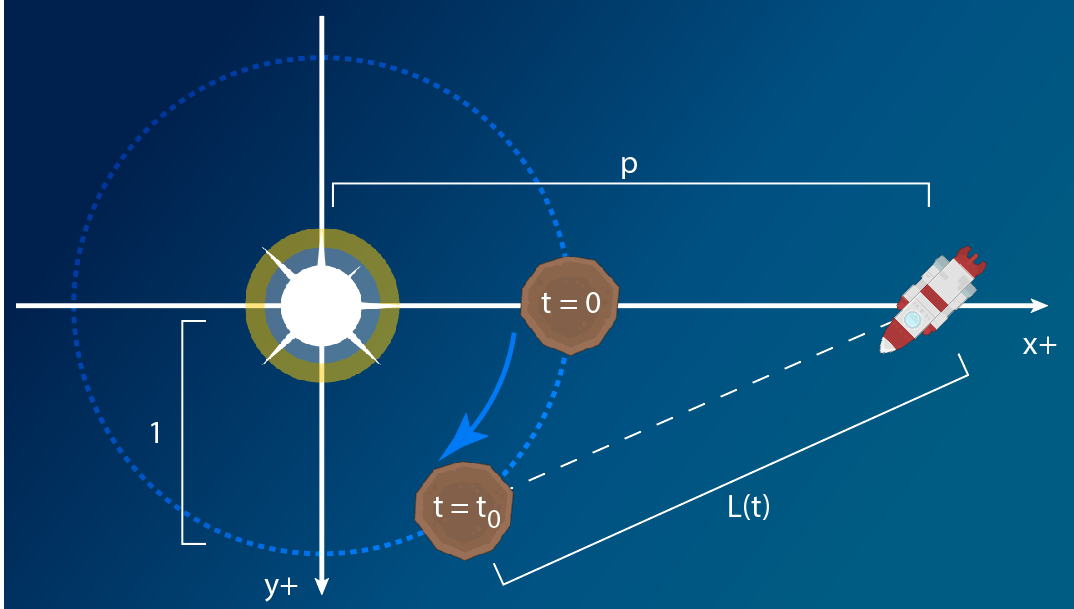
• Define the center of the planet's orbit as the origin

• Define the radius of the orbit as 1 (effectively our distances are now measured in AU)

• Define our unit of time as the duration it takes the planet to travel 1 unit (so now 1 planetary year = 2 pi)

• Define time 0 as the most recent moment that the planet passed between the spaceship's start position and the center of the orbit, and time t_0 is the "start" time when our ship begins moving from that location

This lets us standardize the situation like so:

So our parameters are:

• t_0, the time forward from which we want to find solutions:

   t_0 = angleDifference(planetStartAngle, atan2(shipStartPosition - orbitCenter)) if(t_0 < 0) t_0 += 2 * pi 

• p, the scalar distance of the ship's start position from the center of the orbit:

  p = length(shipStartPosition - orbitCenter)/orbitRadius 

• s, the speed of the ship in our new spacetime coordinate system's scale:

   s = shipSpeed * 2 * pi / (planetAngularSpeed * orbitRadius) 

We're interested in the function L(t), the distance from the ship's start position to the planet.

L(t)² = (p - cos(t))² + sin²(t)
        = p² + 1 - 2p cos(t)

And we want to set this equal to the distance the ship has traveled by time t > 0,

T(t)² = (s(t - t_0))²
        =s²t² - 2s²t*t_0 + s²t_0²

At the times of intercept, T(t) = L(t) so...

s²t² - 2s²t*t_0 + s²t_0² = p² + 1 - 2p cos(t)

Which we can rephrase as:

cos(t) = (1/2p)(-s²t² + 2s²t*t_0 - s²t_0² + p² + 1)

Which is "just" an intersection between a parabola and a garden-variety cosine wave (unscaled, unshifted).

Take the parabola side of that equation and call it P(t). We know we can't possibly have an intersection before P(t) drops to less than or equal to 1, so we can use the garden variety quadratic formula and find the greater of the two solutions P(t_low) = 1 to get a lower bound on t.

We know the cosine wave rises back up to 1 by t_high = t_low + 2pi, but the parabola is strictly decreasing, so our earliest intersection must lie between t_low and t_high, a single wavelength.

We can also find the greatest solution for P(t) = -1 to get a potentially tighter bound on t_high

Unfortunately this seems to be about as far as a pure analytical approach can take us, and we're again forced to use some type of iterative root finding method in this span, but at least we've reduced it to about the simplest case we could hope for.

If your planet orbits much faster than your ship moves, the parabola will be nearly flat in this span and you can closely approximate it as a constant, using acos to find a very close first guess. Or if your ship travels much faster than your planet, the parabola will be nearly vertical the solution will be quite close to t_low. For intermediate cases like the example above, you might be able to approximate each curve as a straight line and iteratively refine from there.